1. Вспомогательная небесная сфера (ВНС)
Основные точки и плоскости на ней. Воображаемая сфера произвольного радиуса, на поверхность которой проецируются видимые места небесных светил вспомогательной небесной сферой (ВНС).
Сфера представляет собой математическую модель для решения задач мореходной астрономии, позволяющую рассматривать светила не в пространстве, а на поверхности сферы.
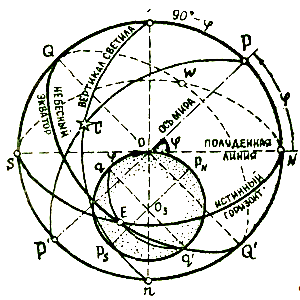
Вертикальная линия Zn, проходящая через центр сферы (точка 0), называется отвесной линией. Её пересечение с поверхностью сферы даёт точки зенита Z и надира n. Плоскость, проходящая через центр небесной сферы перпендикулярно отвесной линии, называется плоскостью истинного горизонта, а линия пересечения этой плоскости с поверхностью сферы называется истинным горизонтом. Линия, проходящая через центр небесной сферы параллельно земной оси РmPs, называется осью мира РР¢. Плоскость, проходящая через центр небесной сферы параллельно плоскости земного экватора, называется плоскостью небесного экватора
Плоскость на небесной сфере, проходящая через полюса мира и точку зенит, называется плоскостью меридиана наблюдателя, или местным небесным меридианом. Плоскость, проходящую через полюса мира и местоположение светила С, называют плоскостью меридиана светила.
Плоскость, проходящий через место светила С и точки зенита и надира называется плоскостью вертикала светил.
2. Порядок построения вспомогательной небесной сферы и нанесения светил на ней
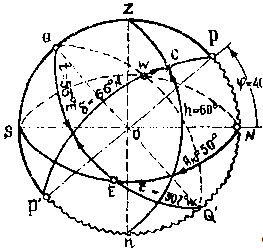
а) из (.) 0 окружность радиусом 4-5 см, которая будет меридианом набл;
б) проводится отвесная линия и обозначаются точки Z и n; в) перпендикулярно отвесной линии проводится горизонтальный диаметр - полуденная линия и большой круг - истинный горизонт. Истинный горизонт проводится от руки в виде эллипса, - если светило в восточной половине горизонта то, точка N пишется справа;
г) от точки горизонта, одноимённой с широтой, на дуге меридиана наблюдателя наносится повышенный полюс мира Р под углом к плоскости истинного горизонта, равным широте места (на рис. j 40°N);
д) через повышенный полюс мира и центр сферы проводят ось мира и обозначают пониженный полюс мира Р´. Полуночную часть меридиана наблюдателя выделяют волнистой линией;
е) перпендикулярно оси мира через центр сферы проводится плоскость небесного экватора. Точки пересечения неб экв с истинным горизонтом обозначают E и W (если смотреть на север, то Е - справа, W - слева). 2. Нанесение видимого места светила на небесную сферу:
а) по известному часовому углу светила (или азимуту, если координата светила задана в горизонтной системе координат) находится точка на небесном экваторе (истинном горизонте), через которую проводится меридиан (вертикал) светила;
б) по дуге меридиана светила (вертикала) отсчитывается от экватора (истинного горизонта) склонение (высота) светила и обозначается его видимое место С.
3. Горизонтная система сферических координат светил. Основные круги и плоскости
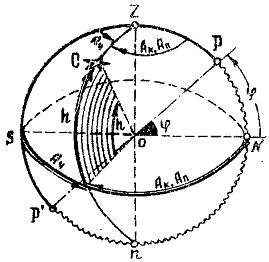
Основными плоскостями горизонтной системы координат являются плоскости истинного горизонта и меридиана наблюдателя, а основными координатами светил - высота h и азимут А светила (рис.1.2). Высотой светила h называется угол при центре небесной сферы между плоскостью истинного горизонта и направлением на светило. Высота измеряется дугой вертикала светила от истинного горизонта до центра светила от 0° до 90°. Если светило С находится над горизонтом, то его высота положительна, а если под горизонтом, то его высота отрицательна и называется снижением светила. Если светило находится на меридиане наблюдателя, то его высота и зенитное расстояние называются меридиональными и обозначаются буквами H и Z . Для Н указывается румб S или N в зависимости от того, в каком направлении от зенита расположено светило. Азимут светила А - это угол в плоскости истинного горизонта между меридианом наблюдателя и меридианом светила. Азимут светила измеряется в круговой (Ак), полукруговой (Ап) или четвертной (Ач) системе координат:
- в круговой системе счёта - от точки N в сторону Е от 0° до 360°;
- в полукруговой системе счёта - от точек N или S в сторону Е или W от 0° до 180°, при этом точка начала отсчёта всегда одноименна с широтой.
- в четвертной системе счёта - от точек N или S в сторону Е или W от 0° до 90°.
4. Первая экваториальная система сферических координат светил
Основные круги и плоскости на ней. Пределы измерения координат светил.
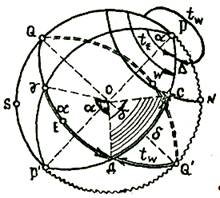
Основными плоскостями яв-ся пл-ти небесного экватора и меридиана наблюдателя. Основные координаты – склонение d и часовой угол t, дополнительная координата - полярное расстояние D=90°-d Обыкновенным или вестовым часовым углом t называется угол в плоскости небесного экватора мира между полуденной частью меридиана наблюдателя и меридианом светила, он измеряется дугой небесного экватора от полуденной части меридиана наблюдателя в сторону запада до меридиана светила от 0° до 360°. Практический часовой угол измеряют от полуденной части меридиана наблюдателя в сторону востока или запада в пределах от 0° до 180°, Практическому часовому углу приписывают наименование Е или W в зависимости от того, к какой половине сферы, восточной или западной, находится светило. При решении задач рекомендуется приписывать наименование к вестовому часовому углу. Если вестовый часовой угол превышает 180°, то он переводится в практический по формуле: tЕ=360°-tw Склонением светила d называется угол при центре небесной сферы между плоскостью небесного экватора и направлением на светило; оно измеряется дугой меридиана светила от экватора до центра светила от 0° до 90° и имеет наименование ближайшего полюса мира. Дугой меридиана от повышенного полюса до параллели светила в пределах от 0 до 180° измеряется полярное расстояние светила; оно наименования не имеет.
5. Вторая экваториальная система сферических координат светил
Основные круги и плоскости на ней. Пределы измерения координат светил.
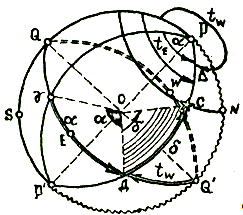
Сферические координаты второй экваториальной системы координат (Рис. 1.3) – склонение d и прямое восхождение a - не зависят от вращения Земли и положения наблюдателя. Основными плоскостями её являются плоскость небесного экватора и плоскость меридиана точки весеннего равноденствия, или точки Овна - точки, в которой 21 марта находится Солнце. Основные координаты - прямое восхождение a и склонение d светила, дополнительные - звёздное дополнение t*=360°-a и полярное расстояние D=90°- d . Прямым восхождением a светила называется угол в плоскости небесного экватора между меридианом точки Овна и меридианом светила. Прямое восхождение измеряется дугой небесного экватора от точки Овна до меридиана светила в сторону, обратную счёту вестовых часовых углов в пределах от 0 до З60°.
Прямое восхождение наименования не имеет, например, на рис. 1.3 a=90°. Прямое восхождение определяет положение меридиана светила относительно точки Овна. Вторая координата - склонение d называется угол при центре небесной сферы между плоскостью небесного экватора и направлением на светило; оно измеряется дугой меридиана светила от экватора до центра светила от 0° до 90° и имеет наименование ближайшего полюса мира.
6. Теоретические обоснования высотной линии положения и её элементов
Малый круг на поверхности Земли или земного глобуса, проведенный из полюса освещения светила сферическим радиусом, равным зенитному расстоянию светила в данный момент времени называется кругом равных высот и является высотной изолинией. На небесной сфере кругу равных высот соответствует круг равных зенитных расстояний.
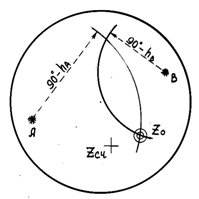
Это определение позволяет обосновать метод нанесения кругов равных высот на земной глобус и определения места судна по высотам светил графическим способом.
Касательная к кругу равных высот, проведенная через определяющую точку перпендикулярно к линии счислимого азимута, называется высотной линией положения (ВЛП). элементы высотной линии положения - счислимый азимут Ас и перенос n=h-hc.
1. Высотная линия положения приближенно совпадает с малым отрезком круга равных высот и проходит через фактическое место судна.
2. Положение влп не зависит от погрешности счислимого места судна, поэтому в качестве счислимых координат можно брать любые координаты вблизи счислимого места.
3. В малых и средних широтах методические погрешности высотной линии положения из-за неучета кривизны линии счислимого азимута и круга равных высот пренебрежимо малы, в высоких широтах и при больших высотах светил, эти погрешности становятся ощутимыми и тем большими, чем больше перенос. При получении большой невязки необходимо повторить вычисление элементов высотной линии положения, приняв за счислимые обсервованные координаты, полученные при первичной обработке.
4. Любая погрешность в измеренной или счислимой высоте вызывает равновеликую погрешность высотной линии положения на местности.
7. Звёздный глобус. Подбор и опознание светил на момент наблюдений.
Звездный глобус является астрономическим вычислительным прибором и представляет собой модель небесной сферы. Он позволяет переходить от одной системы сферических координат к другой с точностью 1,5 -2° или 6 - 8м.
Для опознания неизвестного светила крестовину вертикалов своей оцифрованной стороной устанавливаем на отсчет горизонтального кольца, равный азимуту светила (А=255°). Индекс на крестовине вертикалов устанавливаем на отсчет, равный высоте светила (h=40°). Неопознанная звезда (планета) должна находиться вблизи индекса. Снимаем с глобуса ее название: α Льва.
8. Порядок нанесения на звёздный глобус планет и Луны
Выбираем из МАЕ прямые восхождение и склонения планет:
| Планета | α | δ |
|
Венера Марс Юпитер Сатурн |
85,1° 93,9° 161,1° 100,8° |
N27°37' N 24°38' N 9°24' N 22°42' |
Вращая звездный глобус относительно азимутального кольца (рис. 10), устанавливаем повышенный полюс мира над плоскостью истинного горизонта на угол, равный широте места φс. Наименование повышенного полюса мира всегда совпадает с наименованием широты. Если широта северная то повышенный полюс мира выставляется над N, если южная, то над S. Для установки звездного глобуса по широте на меридиане наблюдателя имеется специальная оцифровка от 0 до 90 градусов;
9. Порядок нахождения и опознания навигационных созвездий и светил
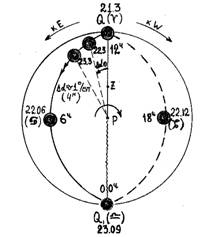
Используя МАЕ расчитываем (рис.10.6) на момент начала утренних навигационных сумерек местное звездное время Sм = tм^:
на Тгр = 00ч10м Sм = tм^ = 250°21,5';
Вращая глобус вокруг оси мира, устанавливаем под меридиан наблюдателя рассчитанное значение Sм = tмγ = 250°21,5'.
Выбираем на звездном глобусе наиболее яркую и легко узнаваемую на небосводе навигационную звезду, в данном случае α Волопаса;
Подводим к светилу крестовину вертикалов, и снимаем с крестовины вертикалов высоту h, а с азимутального кольца азимут светила А:
h=45°, А=231°;
Разворачиваем крестовину вертикалов на угол, равный 90° (для 2 или 4 светил) или 120° (для 3 светил), и вблизи крестовины вертикалов подбираем второе светило, снимаем его высоту и азимут:
α Орла h=30°, А=124°;
Аналогичным образом подбираем третье, а при необходимости и четвертое светило:
Полярная h=57°, А=0°;
Подобранную группу светил наносим на планшет астрономических наблюдений (рис. 10.7).
Для опознания неизвестного светила крестовину вертикалов своей оцифрованной стороной устанавливаем на отсчет горизонтального кольца, равный азимуту светила (А=255°). Индекс на крестовине вертикалов устанавливаем на отсчет, равный высоте светила (h=40°). Неопознанная звезда (планета) должна находиться вблизи индекса. Снимаем с глобуса ее название: α Льва.
10. Принцип построения таблиц ВАС-58 и их устройство
Порядок-вычисления счислимых высот и азимутов светил по таблицам ВАС-58.
Таблицы ВАС-58 (высот и азимутов светил) предназначены для вычисления счислимых высот и азимутов светил. Они являются основным пособием при ручном вычислении счислимых высот и азимутов светил с погрешностями вычислений 0,1¢ и 0,1° соответственно. (Для сравнения: американские таблицы НО № 244 и английские Н.Д. № 486 имеют погрешности вычислений в пять раз больше и значительно уступают в удобстве использования). Таблицы относятся к разряду таблиц готовых ответов. В них приводятся высоты и азимуты на заданное число градусов широт, часовых углов и склонении. Таблицы издаются в 4-х томах для широт от 0° до 80°, разделенных по географической широте и состоят из основных таблиц и таблиц поправок:
По табличным аргументам из основных таблиц выбирают табличные значения (ТЗ) hт, Ат и qт. При одноименных широте и склонению вход в таблицу сверху и слева, при разноимённых - снизу и справа;
Из таблицы 1 выбирают Dhj и DAj по аргументам Dj и Ат, затем по аргументам Dd и qт поправки Dhd и DAd. Вход в таблицу - сверху и слева при положительных разностях Dj и Dd, и снизу и справа -
Рассчитывают сумму поправок азимута сумма DА=DAj+DAd+DAt и вычисляют азимут светила Ас=Ат+åDА. Первая буква наименования азимута в полукруговом счете одноименна с широтой, а вторая – с местным часовым углом;
При h> 60° рассчитывают и вписывают в схему значение (Ас- DАt/2);
Из таблицы 2 по аргументам jс, Dt и Ас или (Ас-DАt/2) выбирают и вписывают в схему поправку высоты за часовой угол; знак поправки противоположен знаку Dt;
Из таблицы 3 по аргументам Ас, Dj и DAd, выбирается и вписывается схему Dhд;
Находится сумма поправок высоты:
åDh=Dhj+Dhd+Dht+Dhд,
и рассчитывается счислимая высота:
hc=ht +åDh,
т.е. счислимая высота равна алгебраической сумме табличного значения высоты, выбранного из основных таблиц ВАС-58 и суммарной поправки высоты, полученной по таблицам поправок. Для среднего наблюдателя время расчета счислимых высот и азимутов светил по таблицам ВАС-58 составляет 4-5 мин, что достигается систематическими тренировками.
11. Суточное движение светил для наблюдателей на экваторе и на полюсе
На Северном полюсе j=90°N, w1=w cos90°= 0, w2=w sin 90°=w=15°/ч,
т.е. на полюсе (рис. 1.10) горизонт не вращается, а плоскость меридиана вращается с угловой скоростью вращения Земли. Это значит, что на полюсе высоты светил не изменяются, а азимуты изменяются c максимальной скоростью 15 градусов в час.

Рис. 1.9. суточное движение светил на экваторе и полюсе рис 1.10.
При суточном вращении Земли конфигурация созвездий на небосводе не изменяется, поэтому их меридианы светил и меридиан точки Овна своего положения в Мировом пространстве не изменяют. Следовательно, прямые восхождения светил из-за их суточного движения не изменяются. Часовые углы светил отсчитываются от полуденной части меридиана наблюдателя, а его плоскость вращается с угловой скоростью вращения Земли. Это вызывает непрерывное возрастание вестовых часовых углов светил с угловой скор около 15°/ч. Для удобства рассуждений в астрономии проще считать неподвижной Землю, а небесную сферу с видимыми светилами - вращающейся в сторону, обратную стороне вращения Земли. Заменяя суточное вращение Земли вращением небесной сферы вокруг оси мира, на сфере будем иметь неподвижными следующие большие круги и точки: - истинный горизонт, - небесный меридиан наблюдателя, - первый вертикал,- полюсы мира, - зенит наблюдателя,- полуденную и полуночную точки небесного экватора. Видимые светила, их меридианы, а также меридиан точки Овна будет вращаться вместе с небесной сферой. Видимое, или кажущееся движение светил, обусловленное вращением Земли вокруг своей оси и имеющее суточный период, называется видимым движением светил.
12. Годовое движение Солнца. Видимое движение Луны. Фазы и возраст Луны
Период одного оборота Земли вокруг Солнца, равный приблизительно 365,25 средних суток - называется тропическим годом.
Видимый путь Солнца по небесной сфере среди звезд за год есть большой круг, плоскость которого наклонена к небесному экватору на постоянный угол ε, равный 23°27' и называемый эклиптикой в течение года Солнце проходит 12 созвездий Эклиптика и небесный экватор пересекаются в двух точках, называемых точками равноденствий. Склонение Солнца в этих точках равно нулю - 21 марта (в точке весеннего равноденствия) - a=0°, d=0°; - 22 июня (в точке летнего солнцестояния) - a=90°, d=23°27¢ N, -23 сентября (в точке осеннего равноденствия) - a=180°, d=0°, - 22 декабря (в день зимнего солнцестояния) - a=270°, d=23°27¢S.
- за месяц до и после дней солнцестояния по 0.1°/сут.;
- за месяц до и после дней равноденствий по 0,4°/сут.;
- в остальное время - по 0,3°/сут.
Луна является спутником Земли и вращается вокруг нее в соответствии с законами И.Кеплера под действием сил тяготения Земли
Промежуток времени, в течение которого Луна совершает полный оборот по орбите относительно звезд, равен 27,32 суток и называется сидерическим, или звездным (Рис. 1.18) месяцем -за период полного обращения Луны по своей орбите ее склонение изменяется от 18°18' до 28°36¢ северного и южного наименования. Фазой Луны наз-тся ее форма освещенной поверхности. Граница между освещенной и неосвещенной частями Луны носит название терминатор Промежуток времени в сутках и их долях от новолуния до данного момента называется возрастом Луны и обозначается буквой В.
13. Звёздное время. Основная формула времени
Промежуток времени между двумя верхними кульминациями точки весеннего равноденствия называется звездными сутками, а число звездных часов, минут, секунд, прошедших от начала звездных суток, называется звездным временем и обозначается латинской буквой S. S = t w^
Повороту небесной сферы на З60° соответствует 24 часа звездного времени, на 180° - 12 часов, на 90°- 6 часов, на 15° - 1 час, на 1°-15 минут Пример:
S=tw^=140°25.4¢=(140/15)ч +(5°∙4+25,4¢/15)мин + (10,4¢∙4)сек =09ч24мин41,6с
Из рис. 2.1 нетрудно заключить, что: S = tw + a (2.2)
т.е. звездное время в данный момент равно вестовому часовому углу любого светила в тот же момент плюс прямое восхождение этого светила. Эта формула называется основной формулой времени, с ее помощью рассчитываются часовые углы звезд:
tw = S-a = S-(360°-t) = S+t*-360°.
Замена a на t* позволила заменить неудобную операцию вычитания более удобным сложением. Отбросив в этой формуле 360°, получим:
tw=S+t*=t w^+t*, (2.3)
т.е. вестовый часовой угол звезды равен часовому углу точки Овна плюс звездное дополнение этой звезды.
14. Истинные и средние солнечные сутки. Уравнение времени
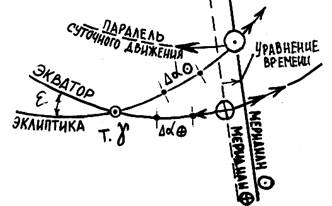
Промежуток времени между двумя последовательными нижними кульминациями центра Солнца называется истинными солнечными сутками. Момент верхней кульминации центра Солнца называют истинным полуднем, а момент нижней его кульминации - истинной полночью.
Чтобы получить постоянную единицу солнечного времени, на небесном экваторе выбрали условную точку - среднее экваториальное Солнце (Рис. 2.4), которое в течение года равномерно движется по экватору в ту же сторону, что и истинное Солнце.
Промежуток времени между двумя последовательными нижними кульминациями среднего Солнца на одном и том же меридиане называется средними, или средними солнечными сутками, а количество средних часов, минут и секунд, прошедших от момента нижней кульминации среднего Солнца до данного момента, называется средним, или гражданским временем и обозначается буквой Т. Уравнение времени Угол между меридианами истинного и среднего Солнца в любой заданный момент называют уравнением времени и обозначают h. h = aÕ - ax = twx- twÕ Если среднее Солнце впереди истинного в суточном движении, то h имеет знак «+», если позади, то «-». Уравнение времени на любую дату можно найти в МАЕ В полдень tгрV= 0°, а tгр выбирается на 12ч из ежедневных таблиц МАЕ, тогда:
h = t гр x- t грÕ = - t грÕ
например, на 11 февраля уравнение времени равно 14мин24с, а на 2 ноября - (-16мин 24с).
15. Местное, декретное, летнее и судовое время, их связь с всемирным (Гринвичским) временем
На каждом земном меридиане в данный физический момент времени - свое собственное местное время, отличающееся от такого же местного времени на другом меридиане на разность долгот.
Вся поверхность земного шара по долготе разбита на 24 часовых пояса. Протяженность одного часового пояса по долготе составляет, 360°/24 = 15° (или 1ч). Меридианы 0°,15°,30°,45°…165°, 180°, то есть кратные 15°, называют осевыми меридианами. Часовым поясам присвоены номера от 0 до 12 к востоку и западу. В нулевом часовом поясе принято всемирное время (гринвичское), а в остальных - местное время осевого меридиана (Рис. 2.11).
В целях экономии электроэнергии, потребляемой на освещение, по декрету Совнаркома от 16 июня 1930 г. все часы в СССР были переведены на 1 час вперед – Декретное время
Тд = Тп+1ч =Тгр +(№+1ч)
После тщательного изучения расхода электроэнергии в утренние и вечерние часы, а также характера деятельности населения постановлением Совета Министров СССР № 925 от 24 октября 1980 г в СССР введено так называемое летнее и зимнее декретное время. Для зимнего времени с I октября по I апреля декретное время Тдз больше поясного на 1 ч, а для летнего декретного Тдл на 2 часа, т.е.
Тдз =Тгр+(№+ 1ч), Тдл =Тгр+(№+2ч). (2.12)
Это значит, что 1 апреля на всей территории Российской федерации ежегодно (начиная с 1981 г.) часы переводят на 1 ч вперед, а 1 октября - на 1ч назад. Декретное время второго часового пояса называется Московским временем. Поясным временем Тп, называется местное время осевого меридиана данного часового пояса, распространенное на всю территорию этого пояса.
Линия, разграничивающая двенадцатые восточный и западный часовые пояса, называется демаркационной линией времени. При переходе судном этой линии происходит необычная смена календарных дат.
Следовательно, меридиан λ=180° разделяет на Земле области с различными календарными датами и новая дата "наступает" на старую с востока на запад со скоростью 15° в час.
Судовым временем Тс называется поясное время того часового пояса, по которому установлены часы на судне.
16. Часовые пояса. Поясное время. Его связь с всемирным (Гринвичским). Линия перемены дат
Вся поверхность земного шара по долготе разбита на 24 часовых пояса. Протяженность одного часового пояса по долготе составляет, 360°/24 = 15° (или 1ч). Меридианы 0°,15°,30°,45°…165°, 180°, то есть кратные 15°, называют осевыми меридианами. Часовым поясам присвоены номера от 0 до 12 к востоку и западу. В нулевом часовом поясе принято всемирное время (гринвичское), а в остальных - местное время осевого меридиана (Рис. 2.11).
Линия, разграничивающая двенадцатые восточный и западный часовые пояса, называется демаркационной линией времени. При переходе судном этой линии происходит необычная смена календарных дат.
Следовательно, меридиан λ=180° разделяет на Земле области с различными календарными датами и новая дата "наступает" на старую с востока на запад со скоростью 15° в час.
17. Судовые измерители времени. Организация службы времени на судне. Порядок расчёта поправки и суточного хода часов (хронометра)
При перемещении судна к востоку по долготе на 75° разница судового и местного времени составит 75°/15°=5ч и побудка на судне придется на полдень, обед - на вечер, а отбой - к утру следующих местных суток. Неверно выбранный счет судового времени приведет к физиологическому и психологическому перенапряжению экипажа судна.
Судовым временем Тс называется поясное время того часового пояса, по которому установлены часы на судне, и по которому организована повседневная деятельность экипажа:
Тc =Тгр±№сEW (2.13)
где №с - номер часового пояса, поясное время которого принято в качестве судового. Поскольку
Тгр=Тм±λEW,
то для расчета судового времени по заданному местному времени применяется формула:
Тc=Тм ± λEW №сEW=Тм ± (№с - λ) EW (2.14)
На судах, снабженных хронометрами или палубными часами, всемирное время должно быть известно с точностью до 0,5с. Для обеспечения повседневной жизни экипажа корабля судовое время достаточно измерять о точностью до 1 мин, а показания корабельных часов и часов членов экипажа судна - с точностью до 0,5 мин.
Служба времени на судне организуется с целью обеспечения повседневной деятельности экипажа судна точным единым временем и предусматривает: - определение точного времени, т.е. учет поправок хронометров и часов, - техническую эксплуатацию измерителей времени (завод, проверка, регулировка, ремонт); - ведение эксплуатационной документации - журнала хронометра и часов, журнала проверки морских часов, формуляра СЕВ; - регулярный прием информации о разности шкал эталонного и всемирного времени ΔТк и учет ее по мере необходимости; - хранение эталонного времени СЕВ и учет изменения поправки хронометра до следующего приема радиосигналов времени; - распространение информации о точном времени на командные пункты и судовые посты с помощью цифровых и стрелочных индикаторов. За организацию службы времени на судне, как правило, отвечает один из вахтенных помощников капитана.
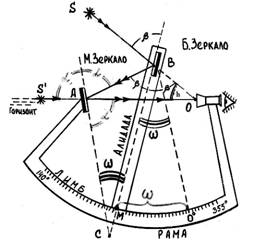
18. Навигационный секстан. Принцип измерения высот светил
Навигационным секстаном называется оптический угломерно-отражательный прибор, предназначенный для измерения вертикальных и горизонтальных углов по принципу совмещения изображений.
Принцип действия секстана основан на использовании двух законов оптики:
1. Угол падения луча в плоское зеркало равен углу его отражения от зеркала.
2. Падающий и отраженный лучи лежат в одной плоскости с перпендикуляром к плоскости зеркала, восстановленном в точке падения луча. Пусть необходимо измерить угол h между линией видимого горизонта и направлением на светило С (рис. 5.1).
На пути луча от светила установим большое зеркало В, а на пути луча от видимого горизонта - малое полупрозрачное зеркало А так, чтобы наблюдатель из точки 0 через него видел линию видимого горизонта. Плоскости обоих зеркал перпендикулярны плоскости чертежа.
19. Поправка индекса секстана, способы её определения. Контроль точности определения индекса по Солнцу. Общая поправка секстана
Определение поправки индекса по Солнцу. Более точно поправка индекса определяется по Солнцу, причем здесь появляется возможность проконтролировать качество наблюдений:
1. Установить отсчет секстана равно 0º.0´.
2. Подобрать светофильтры на оба зеркала.
3. Навести секстан на Солнце
4. Вращая отсчетный барабан, добиться совмещения краев прямовидимого и отраженного дисков Солнца, так чтобы отраженное изображение было выше прямовидимого (Рис. 5.14) и снять отсчет ОС1. Затем отраженное изображение перевести в нижнее касание и снять отсчет ОС2.
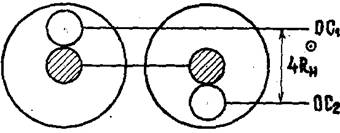
Рис. 5.14. Определение поправки индекса по Солнцу.
5. Рассчитать средний отсчет секстана: ОСср=(ОС1+ОС2)/2 .
6. Рассчитать поправку индекса: i=360°-ОСср.
7. Рассчитать видимый радиус Солнца: R=(ОС1-ОС2)/4.
8. Выбрать из МАЕ или из ВАС-58 на дату наблюдений фактический радиус Солнца. 8. Сравнить рассчитанный радиус Солнца с фактическим, оценив тем самым качество наблюдений. Если эта разница превышает 0.2' , то наблюдения необходимо повторить.
Из ежедневных таблиц МАЕ на 21 февраля выбираем R=16,2¢. Разница cоставляет 0,1¢, поэтому качество наблюдений хорошее. Если поправка индекса превышает 5¢, то ее рекомендуется уменьшить. Истинная выс звезды h*ист=oc+(i+s)+Dhd+Dhr+Dht +Dhв
20. Навигационный секстан. Его устройство и правила обращения с ним.
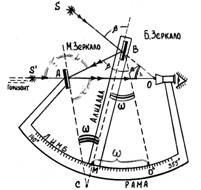
1. Осторожно за раму вынуть секстан из ящика и, взяв его за ручку в правую руку, произвести осмотр.
2. Отфокусировать по видимому горизонту трубу и установить ее на место. Окулярную часть дневной трубы установить так, чтоб одна пара ее нитей была параллельна, а другая - перпендикулярна плоскости лимба.
3. Установить лупу осветителя по глазу, а для наблюдений Солнца подобрать светофильтры.
4. Произвести выверки навигационного секстана.
6. Определить поправку индекса.
21. Навигационный секстан. Его устройство и правила обращения с ним. Порядок выверки параллельности оптической оси астрономической трубы к плоскости лимба
1. Осторожно за раму вынуть секстан из ящика и, взяв его за ручку в правую руку, произвести осмотр.
2. Отфокусировать по видимому горизонту трубу и установить ее на место. Окулярную часть дневной трубы установить так, чтоб одна пара ее нитей была параллельна, а другая - перпендикулярна плоскости лимба.
3. Установить лупу осветителя по глазу, а для наблюдений Солнца подобрать светофильтры.
4. Произвести выверки навигационного секстана.
6. Определить поправку индекса.
а. Проверка параллельности оси зрительной трубы плоскости лимба.
1.Установить секстан на ящик и на края лимба установить диоптры так, чтобы соединяющая их линия была параллельна оси трубы;
2. Привести в створ срезов диоптров ориентир, удаленный на 50 м и более (удобно использовать линию видимого горизонта). При наблюдении в трубу этот ориентир должен находиться в середине сетки нитей трубы (Рис. 5.8). Если ориентир не в середине сетки, то параллельность оси трубы нарушена (Рис. 5.7).
3. Если параллельность оси трубы нарушена (Рис. 5.7), то необходимо отверткой поджать или отдать регулировочные винты на кольце трубы и привести ориентир в середину поля зрения трубы.
22. Навигационный секстан. Его устройство и правила обращения с ним. Порядок выверки перпендикулярности большого зеркала к плоскости лимба
1. Осторожно за раму вынуть секстан из ящика и, взяв его за ручку в правую руку, произвести осмотр.
2. Отфокусировать по видимому горизонту трубу и установить ее на место. Окулярную часть дневной трубы установить так, чтоб одна пара ее нитей была параллельна, а другая - перпендикулярна плоскости лимба.
3. Установить лупу осветителя по глазу, а для наблюдений Солнца подобрать светофильтры.
4. Произвести выверки навигационного секстана.
6. Определить поправку индекса.
б. Проверка перпендикулярности большого зеркала плоскости лимба.
1. Снять трубу, секстан поставить на ящик, алидаду установить на отсчет около 35°;
2. На лимб на отсчеты 0° и 130° установить диоптры срезами вверх;
3. Откинуть светофильтры и с расстояния 20-30 см от большого зеркала наблюдать в него под острым углом, чтобы у правого среза зеркала видеть прямовидимое и отраженное изображение диоптров. Если один из диоптров не виден, необходимо передвинуть его или алидаду;
4. Верхние срезы обоих диоптров должны образовать прямую линию (Рис. 5. 10). При изломе срезов диоптров перпендикулярность большого зеркала нарушена (Рис. 5.9). С точностью до 10¢ эту проверку можно провести по дуге лимба.
5. Если перпендикулярность большого зеркала нарушена (Рис. 5.9), то необходимо торцевым ключом ослабить или подтянуть верхний регулировочный винт большого зеркала и установить срезы диоптров по прямой линии (Рис. 5.10).
23. Навигационный секстан. Его устройство и правила обращения с ним. Порядок выверки перпендикулярности малого зеркала к плоскости лимба
1. Осторожно за раму вынуть секстан из ящика и, взяв его за ручку в правую руку, произвести осмотр.
2. Отфокусировать по видимому горизонту трубу и установить ее на место. Окулярную часть дневной трубы установить так, чтоб одна пара ее нитей была параллельна, а другая - перпендикулярна плоскости лимба.
3. Установить лупу осветителя по глазу, а для наблюдений Солнца подобрать светофильтры.
4. Произвести выверки навигационного секстана.
6. Определить поправку индекса. в. Перпендикулярность малого зеркала плоскости лимба.
1. Подготовить секстан к наблюдениям и установить алидаду на отсчет около 0°;
2. Навести трубу на светило и вращением отсчетного барабана перевести алидаду через ноль шкалы лимба, наблюдая за изображением светила. 3. При перпендикулярности малого зеркала к плоскости лимба дважды отраженное изображение светила совпадет с прямовидимым. Если перпендикулярность нарушена, то отраженное изображение находится в стороне от прямовидимого (Рис. 5.11).
4. Вращением регулировочных винтов малого зеркала торцевым ключом совместить отраженное изображение светила с прямовидимым (Рис. 5.12).
24. Сущность поправки видимой высоты за полудиаметр светила
Влияние того, что при измерениях высот Солнца и Луны, как правило, измеряется высота верхнего или нижнего края светила компенсируется учетом поправки за радиус светила R (Рис. 5.13):
- Для Солнца значение R выбирается либо из МАЕ на заданную дату, либо из таблиц ВАС-58 и ТВА-57. При измерениях нижнего края светила данной поправке присваивается знак «+», при измерениях нижнего края - знак «-». - Для Луны поправка Rƒ включена в общую поправку высоты Луны (5.9). Таким образом истинная высота светила рассчитывается по формуле:
hист=oc+(i+s)+Dhd+Dhr+Dht+DhB+DhP+Rƒ (5.10)
Итак, конкретно для каждого высоты светил исправляются следующими поправками:
- для звезд h*ист=oc+(i+s)+Dhd+Dhr+Dht +Dhв (5.11)
- для Солнца hист=oc+(i+s) +Dhd+Dhr+р+Dht+Dhв (5.12)
- для Луны hƒист=oc+(i+s)+Dhd+Dht+Dhв+Dhƒоп (5.13)
25. Сущность поправки измеренной высоты светила за наклонение видимого горизонта
Разница между видимым горизонтом и истинным компенсируется поправкой за наклонение видимого горизонта Dhd. Поправка Dhd, приводит высоту светила, измеренную над видимым горизонтом, к видимой высоте над истинным горизонтом (рис. 5.13). Луч от линии горизонта Г проходит в глаз наблюдателя по криволинейной траектории ГО, а кривизна ее зависит от состояния приземного слоя атмосферы и возвышения глаза наблюдателя над уровнем моря. Наблюдатель видит линию горизонта по направлению касательной ОВ к траектории луча. Наклонение горизонта - угол между истинным и видимым горизонтом, по величине неустойчиво, особенно в закрытых морях, у побережья, у границы льдов и в местах встречи теплых и холодных течении. В этих районах величина наклонения может изменятся относительно табличного до 2-4 угловых минут, поэтому при астрономических наблюдениях наклонение рекомендуется измерять специальным прибором - наклономером типа Н-5. При невозможности измерения поправка за наклонение видимого горизонта выбирается из таблицы 3.21 МТ-2000 (11-а МТ-75 и подобных таблиц в МАЕ, ВАС-58, ТВА-57), рассчитанных по формуле:
![]() (5.6)
(5.6)
где е – высота глаза наблюдателя над уровнем моря (м).
Dhd= -0,04136Дп-18,562е /Дп
где Дп - расстояние до уреза воды или до судна (кбт).
26. Сущность поправки видимой высоты светила за астрономическую рефракцию
Поправка за астрономическую рефракцию Dhr, исключает влияние атмосферы, искривляющей траекторию луча от светила СО, в результате чего светило наблюдается по касательной ОС' к траектории луча. Для температуры воздуха +10° С и атмосферного давления 760 мм. рт. ст. поправка на астрономическую рефракцию приведена в таблице 3.22 МТ-2000 (9-а МТ-75 и подобных таблиц в МАЕ, ВАС-58, ТВА-57), рассчитанной по формуле:
Dhr =- 0,97¢ctghв (5.7)
где hв – видимая высота светила. При отклонении фактических метеоусловий от средних, принятых при составлении этой таблицы, необходимо дополнительно учесть две поправки:
- поправку высоты светила за температуру воздуха Dht. Выбирается из таблицы 3.24 МТ-2000, 14-а МТ-75 и из подобных таблиц в МАЕ, ВАС-58, ТВА-57.
- поправку высоты за давление воздуха Dhв. Выбирается из таблицы 3.25 МТ-2000, из таблицы 14-6 МТ-75 и из подобных таблиц в МАЕ, ВАС-58, ТВА-57. Поправка на астрономическую рефракцию Dhr+Dht+Dhв стабильнее поправки за наклонение горизонта, так как луч от светила идет на большом удалении от подстилающей земной поверхности в более стабильных слоях атмосферы, исключение представляют лучи светил, расположенных близко к горизонту. Отклонение величины этой поправки при высоте светила до 5° достигает 0,3-1,0 угловых минуты, поэтому наблюдать светила на малой высоте не рекомендуется.
27. Сущность поправки видимой высоты светила за параллакс
Поправка за параллакс DhP компенсирует тот факт, что измерения высоты светила производятся с поверхности Земли, а не из ее центра (центра вспомогательной небесной сферы). Она приводит топоцентрическую высоту светила hт с поверхности Земли к геоцентрической высоте из её центра. Из СОО3 (Рис. 5.13) по теореме синусов имеем:
sinDhP /sin (90°+hт)=R/CO3,
Откуда:
sinDhP=(R/CO3) coshт.
При hт =0 и j =0, R/CO3 = sinр0,
где р0 - горизонтальный экваториальный параллакс "светило-угол", под которым со светила, находящегося на горизонте, виден земной радиус, поэтому: sinDhP= sinр0coshT (5.8) Звезды находятся за пределами Солнечной системы на очень большом расстоянии и направления на них как из центра Земли, так и c ее поверхности будут практически одинаковым, то есть для звезд поправкой за параллакс вследствие ее ничтожности можно пренебречь. Более того, из светил Солнечной системы (планеты, Солнце и Луна) данной поправкой можно пренебречь для самых далеких от Земли планет – Юпитера и Сатурна. Для планет (Венеры и Марса) поправка за параллакс приведена в таблице 3.23 МТ-2000 (9-б МТ-75 и в подобных таблицах МАЕ, ВАС-58, ТВА-57).
Для Солнца поправка за параллаксDhP включена в суммарную поправку за рефракцию и параллакс Dhr+р и приведена в таблице 3.26 МТ-2000 (в подобных таблицах МАЕ, ВАС-58, ТВА-57): Dhr+р= Dhr+DhP Для Луны поправка DhP включена в общую поправку высоты Луны:
Dhƒоп= Dhr+Dh P±Rƒ (5.9)
где Rƒ - топоцентрический полудиаметр Луны.
28. Назначение и содержание морского астрономического ежегодника (МАЕ)
Порядок вычисления местного часового угла и склонения светил. Морской астрономический ежегодник (МАЕ) предназначен в основном для вычисления часовых углов и склонений светил на момент их наблюдения, а также для получения других астрономических данных, необходимых для судовождения. Часовые углы звезд в МАЕ непосредственно не приводятся. Для их получения используют формулы (2.3) и (2.6):
tW =Sм+t*= tWγ +t*=(tгр ± lEW)+t*,
следовательно, вестовый часовой угол звезды равен вестовому часовому углу точки Овна плюс звездное дополнение этой звезды. Из этого правила следует: чтобы вычислить часовой угол звезды, надо рассчитать местное звездное время, изменяемое вестовым часовым углом точки Овна и сложить его с звездным дополнением звезды.
Западный часовой угол. Для звёзд
tW=tм^ +t*,
для Солнца, Луны и планет
tW=tгр ± lwЕ
- если часовой угол tW получается меньше 180°, то расчет часового угла на этом заканчивается;
- если часовой угол tW получается больше180°, но меньше 360°, то он переводится в практический часовой угол tЕ = 360°- tW; - если часовой угол tW получается больше 360°, то из результата вычитается 360° и наименование часового угла при этом не изменяется (остаётся tW!). tЕ = 360°- tW. Находится только при 180° < tW < 360°
Табличное значение склонение d светила и его наименование. Выбирается из ЕТ по целому часу ТГгр и дате для соответствующего светила. Для звезд не рассчитывается.
Поправка склонения. Выбирается из ОИТ на странице минут в колонке “Попр.” по D. Знак одинаков Dd со знаком D. Для звезд не рассчитывается
Склонение светила. Для Солнца, Луны и планет
d=dт+Dd.
Для звёзд d выбирается либо из таблицы “Звёзды. Видимые места” (для всех навигационных звезд, при этом данные приведены на первое число каждого месяца), либо из раздела “Звёзды. Видимые места” ежедневных таблиц (только для наиболее ярких звезд, при этом данные приведены на середину трехсуточного интервала).
29. Порядок исправления измеренных высот светил
полученный с помощью навигационного секстана отсчет ОС не является истинной высотой светила вследстве влияния следующих причин:
- несовпадение нулевого отсчета лимба и отсчета секстана ОС;
- заводских и эксплуатационных погрешностей секстана;
- измерения высот светил производятся относительно видимого горизонта, а не истинного;
- видимое направление на светило не совпадает с истинным вследствие преломления лучей в атмосфере (явление рефракции);
- измерения высоты светила производятся с поверхности Земли, а не из ее центра (центра вспомогательной небесной сферы);
- при измерениях высот Солнца и Луны измеряется, как правило, высота верхнего или нижнего края светила.
- для звезд h*ист=oc+(i+s)+Dhd+Dhr+Dht +Dhв
- для Солнца hист=oc+(i+s) +Dhd+Dhr+р+Dht+Dhв
- для Луны hƒист=oc+(i+s)+Dhd+Dht+Dhв+Dhƒоп
- для Марса h♂ист=oc+(i+s)+Dhd+Dhr+Dht+Dhв+DhP
- для Венеры h♀ист=oc+(i+s)+Dhd+Dhr+Dht+Dhв+DhP+Dhф
где Dhф=с·cos[180°-(G+q)]=с·cosq – поправка высоты за фазу Венеры, выбираемая из МАЕ.
30. Определение места судна по разновременным измерениям высоты светила (Солнца)
В светлое время суток мореплаватель имеет возможность одновременно наблюдать только одно светило - Солнце. для получения астрономической обсервации приходится пользоваться методом его разновременных наблюдений. Промежуток времени между двумя наблюдениями определяется необходимостью изменения азимута светила на угол 40°-50°, который изменяется со скоростью: DА= 5°/ч (sin j-cos j cosA tgh). При этом условии высотные линии положения, которые перпендикулярны азимутам на светило, пересекутся под углом 40°-50°, обеспечивая высокую надежность обсервованного места.
Предположим, что в момент первых наблюдений Т1 счислимое место судна находилось в точке МС1 (рис. 8.13). Его обсервованное место в этот же момент должно располагаться на высотной линии положения I-I, элементы которой Ас1 и n1=(h1 – hс1), были получены по счислимым координатамточки Мс1, т.е. по φс1 и λ с1. Через 2-4 часа на средний момент времени Т2, совершив плавание S=V- (Т2-Т1) на судне провели вторые наблюдения Солнца и получили высотную линию положения ІІ - ІІ. Элементы этой линии положения Ас2 и n2=(h2-hс2) были вычислены по координатам второй счислимой точки Мс2. Можно утверждать, что в момент вторых наблюдений Т2 место судна находилось в одной из точек линии ІІ- ІІ.
Будем считать, что при плавании судна между двумя наблюдениями не было допущено никаких погрешностей счисления. Перенесем высотную линию положения I-I по направлению пути судна на величину плавания S. Очевидно, что в момент Т2 вторых наблюдений обсервованное место при условии точного счисления должно находится где-то на этой перенесенной линии положения I'- I'. Но так как в этот же момент судно находится на линии положения II-II, то точка Мо пересечения линий положения I'- I' и II-II и явится его обсервованным местом.
31. Определение места судна по одновременным измерениям высот светил
Термин "одновременные наблюдения" означает, что измерение серий высот двух и более светил выполнено в быстрой последовательности, при этом разность средних моментов времени последней и первой серии не превышает 10-15 мин. За этот интервал времени судно пройдет расстояние не более 10 миль, следовательно при приведении высот светил к одному моменту наблюдений, относительно которого вычисляются элементы высотных линий положения, не требуется учитывать сферичность Земли и погрешности счисления. Определение места судна по двум светилам, наблюдаемым одновременно, можно производить днем по Солнцу и Луне, по Солнцу и Венере, по Луне и Венере, а в сумерки - по двум звездам. Самое удобное время для наблюдений звезд и планет - период навигационных сумерек, который рассчитывается заранее либо с помощью МАЕ, либо с помощью вычислительной техники. Вечерние наблюдения надо начинать сразу после захода Солнца, стараясь через трубу секстана обнаружить наиболее яркие светила, прежде чем они будут видны невооруженным глазом. Утром измерение высот ярких звезд желательно производить ближе к концу навигационных сумерек. Измеренные при этих условиях высоты будут наиболее надежными, так как хорошо видна линия горизонта. Обсервованое место судна получается в точке пересечения двух высотных линий положения (Рис.6.6), которые пересекаются под углом Θ=Ас2-Ас1. Для получения высокой точности обсервации наиболее благоприятная комбинация светил для наблюдений - по высотам 20°-60° при разности азимутов, близкой к 90°, но не менее 30°.
Две высотные линии положения всегда пересекаются в одной точке, поэтому по такой обсервации невозможно обнаружить и оценить неизбежные погрешности наблюдений, ошибки вычислений и промахи. Для получения более точного и надежного места необходимо иметь три или четыре высотные линии, по которым легко обнаружить промахи, оценить и исключить влияние систематических (повторяющихся) погрешностей высотных линий положения. Третья (избыточная) высотная линия положения повышает точность обсервации примерно на 15-20%. Высотные линии положения приводят к моменту наблюдений последней высоты. На этот момент и получаем обсервованное место судна.
32. Определение обсервованной широты по высоте Полярной
В северном полушарии при широтах 5°-74° удобной звездой с точки зрения объема вычислений является Полярная - звезда α Малой Медведицы. Известно, что высота повышенного полюса мира равна географической широте места судна. Вблизи Северного полюса мира расположена Полярная звезда, которая имеет экваториальные координаты δ@89,2°N и α@33,9°. В своем суточном движении она описывает параллель радиуса ∆=90°-δ@0,8° (рис. 9.3).
33. Нахождение вероятного обсервованного места в фигуре погрешностей
Метод наименьших квадратов – отыскивание таких значений ∆φ и ∆λ при которых сумма квадратов невязок будет величиной мин.
Весом называется величина обратная квадрату СКП Р=1/m2 P=P1 +P2 Mв= √1/р Способ весов используется при нахождении вероятнейшего места судна по силе одновременных разнообразных обсерваций.
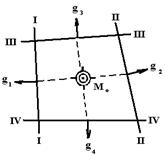
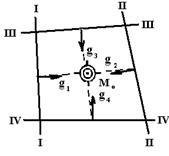
Рис. 7.8. Нахождение вероятнейшего (вероятного) места судна с учетом только случайных погрешностей способом противомедиан.
Нахождение вероятнейшего (вероятного) места судна в четырехугольнике погрешностей.
34. Организация наблюдения и измерения высот светил
1 этап. Подготовка к наблюдениям: - оценка астронавигационной обс-ки и подбор светил для набл;
- выбор времени и места наблюдений;
- определение поправки индекса навигационного секстана:
i=360°- ос(осср);
- определение поправки часов:
Uхр=Uхр2+ω0 (Т-Т2), сл= Тхр -Тч, Uч =Uхр+сл
2 этап. Астрономические наблюдения:
- измерение серий высот и времени, снятие времени наблюдений Т и отсчета лага ОЛ; - Снятие с карты счислимых координат;
3 этап. Обработка наблюдений:
- запись наблюдений в навигационный журнал по форме:
21.05 ол=15,0 α Близнецов ос=32°15,8'; i+s=-1,3'; T=17ч 03мин32с; α Ориона ос= 25°16,5'; i+s =- 1,2'; Т=17ч04мин48с; Uч =+27с; е=10м; tв=+5°; Вв=742 мм рт.ст.. - расчет средних значений ос и времени:
ОСср=åОСi / n, Тср=åТi / n;
- Расчет часовых углов t и склонений светил d;
- Расчет счислимых высот светил hс;
- Расчет истинных высот светил hист.;
- Приведение высот светил к одному месту наблюдений (к одному зениту) - расчет поправки Δhz;
- Расчет элементов высотных линий положения:
Ас1, n1=(h+Δhz)-hc1; Ас2, n2=(h-hc2);
- Прокладка высотных линий положения и расчет координат обсервованного места.
небесный светило навигационный судовой
35. Определение поправки компаса по небесным светилам
DК=ИП-КП
В мореходной астрономии истинный пеленг светила представляет собой его азимут в круговом счете Ак. Компасный пеленг определяют при наблюдениях как средний из трех-пяти компасных пеленгов на светило с фиксацией моментов времени Тч каждого измерения:
КП=å КПi/n, (10.2)
Тч =åТчi /n. (11.3)
Исходя из приведенных ваше рассуждений и на основании рис. 10.2 для различных курсоуказателей получим:
DК=Aк-КПк=Ак-(КК+КУ*) (11.4)
Азимут светила вычисляется из параллактического треугольника (рис. 11.2.), и в общем случае является функцей трех аргументов (§ 4.1):
А=f1(φ, δ, tм)= f2(φ, δ, h)= f3(φ, h, tм) (11.5)
В зависимости от способов получения аргументов в выражении 11.5 существуют несколько способов расчета поправки курсоуказания астрономическим способом.
Способ моментов. азимут светила вычисляетя по первой зависимости формулы 11.5, то есть используются аргументы φ, δ и tм. Для вычисления склонения δ и местного часового угла tм с помощью МАЕ, либо вычислительной техники, замечается момент времени с точность до одной секунды (универсальность и достаточно высокая точность, его можно применять в любое время суток по отношению к любому наблюдаемому светилу.)
Способ высот. В данном способе азимут светила вычисляетя по второй зависимости формулы 11.5, то есть используются аргументы φ, δ и h. Способ предполагает, что при пеленговании светила была измерена, или заранее вычислена его высота h. Азимут светила в данном случае вычисляется с помощью вычислительной техники.
Способ высот и моментов. В данном способе азимут светила вычисляетя по третьей зависимости формулы 11.5, то есть используются аргументы φ, h, и tм. Этот способ используется при совмещении определения поправки курсоуказания с определением места судна, как правило, с помощью астронавигационной системы
36. Сущность астрономических явлений, связанных с освещённостью горизонта. Расчёт элементов освещенности горизонта
Состояние освещенности оказывает существенное влияние на повседневную деятельность судна: в ночное время снимается точность и надежность радионавигационных, систем, технических средств наблюдения и связи, существенно возрастает количество аварий. Сумерками называется период времени плавного перехода от дневного света к ночной тьме (и наоборот). Видимым восходом (заходом) Солнца называется момент пересечения верхним краем Солнца линии видимого горизонта. Высота Солнца при этом составляет h=-50.3¢. Момент видимого захода Солнца соответствует началу вечерних гражданских сумерек, а момент видимого восхода Солнца соответствует окончанию утренних гражданских сумерек.
После прихода центра Солнца на высоту (- 6°) линия горизонта видна хорошо, отчетливо различаются береговые ориентиры, но звезды уже почти не наблюдаются.
Наиболее предпочтительным периодом для наблюдения звезд является период с середины гражданских до середины навигационных сумерек.
Теоретически время видимого восхода и захода, кульминации Солнца или Луны, начала утренних и конца вечерних сумерек можно вычислить по формуле
соs tм = sес j sес d sin h - tg j tg d,
Азимуты видимого восхода или захода Солнца вычисляют по таблице 3.37 МТ-2000 (или по таблицам 20а и 20б МТ-75)
высота Солнца в момент видимого восхода или захода изменится на величину:
Dh= Dhd + Dht+Dhв.
37. Определение поправки компаса по Полярной звезде
При плавании судна в малых и средних широтах (j =5-25°N) удобным астроориентиром для определения поправки курсоуказания является Полярная звезда. Для нее по рис. 11.4 из сферического треугольника СZР по теореме синусов имеем:
sin А=cos d sin tм sec h.
Но для Полярной можно принять sec h @ sес j и по малости углов А и D sin A@А , sinD@D, a tм=tм - a= t M -33°, тогда:
A = D sec j sin(tм- 33°). (11.9)
По этой формуле рассчитана и помещена в МАЕ таблица “Азимут Полярной’’. Входными аргументами этой таблицы являются широта места судна φс и местный часовой угол точки Овна tм^. Из рис. 11.4 и формулы (11.9) видно, что при tм=33° Полярная имеет верхнюю кульминацию, а при tм =33°+180°=213° - нижнюю кульминацию и в эти моменты азимут Полярной равен нулю. При часовом угле точки Овна в пределах 33°-180°-213° Полярная будет в западной части сферы и наименование азимута будет NW, а при значении 213°-0°-33°- NE. Точность вычисления азимута в данном случае mА=0,1°. Азимут Полярной звезды изменяется очень медленно, поэтому при обычном порядке наблюдений моменты времени можно замечать с точностью до 1 минуты и измерение пеленгов может производить один наблюдатель. Таким образом определение поправки курсоуказания по Полярной является частным случаем способа высот и моментов.
38. Определение и порядок действий при определении поправки компаса по видимому восходу (заходу) Солнца
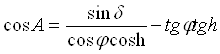 . (11.7)
. (11.7)
Из формулы 11.7 видно, что азимут светила легко найти, если известна его высота. Если в качестве светила взять Солнце, а компасный пеленг его измерять в момент восхода или захода верхнего края Солнца, то его высота в этот момент будет равна:
h= h`+ Dhd+Dhr+Dhp- R=0°00.0¢ - 6.1¢ - 35.7 ¢- 16.0¢ = -57.8¢,
где Dhd расчитана для высоты глаза наблюдателя е=12 м. Для такой высоты Солнца формула 11.7 преобразовывается к виду:
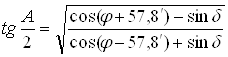 . (11.10)
. (11.10)
По этой формуле рассчитаны и помещены в таблице 3.37а и 3.37б МТ-2000 (в таблицах 20-а и 20-б МТ-75) "Азимуты видимого восхода или захода верхнего края Солнца ". Входными аргументами таблиц являются широта места и склонение Солнца. Первая буква наименования азимута в полукруговом счете одноимённа с широтой, вторая Е - при восходе и W - при заходе Солнца. Из-за нестабильности поправок Dhd и Dhr СКП расчета счислимого азимута по этим таблицам mA=0,3°. Таким образом определение поправки курсоуказания по видимому восходу и заходу Солнца является частным случаем способа высот. Пеленгование Солнца в данном случае производится не серией, а однократно, при этом момент времени замечается с точностью до 1 мин.
39. Определение обсервованной широты места судна по меридиональной высоте Солнца
Данный способ привлекает внимание своей простотой и малым объемом вычислений.
В процессе видимого суточного движения светило дважды пересекает плоскость меридиана наблюдателя. высота светила будет наибольшей в момент верхней кульминации и наименьшей в момент нижней кульминации.
Если в момент измерения наибольшей высоты Солнца заметить гринвичское время, то с помощью МАЕ (а в аварийном случае и без него) можно получить склонения Солнца на момент наблюдений.
jо =(90°- H) ±dNS (9.9)
т.е. обсервованная широта равна меридиональному зенитному расстоянию плюс-минус склонение светила, причем знак "плюс" берется при одноимённых широте и склонению, а знак "минус" - при разноимённых.
Если измерялась наименьшая высота Солнца H', что возможно при полярном дне, то:
jо =(90°- d) +H'
Последовательность действий при определении широты по измеренной меридиональной высоте Солнца.
1. Засчитать с помощью МАЕ судовое время кульминации Солнца и снять с морской навигационной карты счислимте координаты судна φс и λс на этот момент;
2. Подготовить секстан к дневным наблюдениям и определить по Солнцу поправку индекса i;
3. Измерить, если это возможно, наклонение видимого горизонта d;
4. За 5-7 минут да рассчитанного времени кульминации начать измерять высоты Солнца. Измерения прекратить после получения двух-трех убывающих отсчетов. Одновременно зафиксировать время измерения наибольшей высоты с точностью до 1 минуты;
5. Заметить, над какой точкой горизонта измерялась высота Солнца – N или S (измерить компаний пеленг на светило);
6. Рассчитать по рассмотренной выше методике обсервованную широту места судна.
40. Определение обсервованной широты места судна по высоте Полярной
В северном полушарии при широтах 5°-74° удобной звездой с точки зрения объема вычислений является Полярная - звезда α Малой Медведицы. Известно, что высота повышенного полюса мира равна географической широте места судна. Вблизи Северного полюса мира расположена Полярная звезда, которая имеет экваториальные координаты δ@89,2°N и α@33,9°. В своем суточном движении она описывает параллель радиуса ∆=90°-δ@0,8° (рис. 9.3).
| Полярная | |
| 1 попр. | ТАБЛ.1 МАЕ по tм^ |
| 2 попр. | ТАБЛ. ΙΙ МАЕ по tм^ и h |
| 3 попр. | ТАБЛ. ΙΙΙ МАЕ по tм^ И ДАТЕ |
| Σ | Ι + ΙΙ + ΙΙΙ |
| Прив.h | Ист. h+Δhz |
| φ0 | Прив.h+ Σ |
41. Назначение, принцип действия, состав, основные ТТХ низкоорбитных СНС. Принцип получения навигационного параметра
Спутниковая (космическая) навигационная система (СНС) предназначена для высокоточного определения координат места и составляющих скорости наземных, морских, речных, воздушных и других подвижных объектов в любой точке земного шара.
К низкоорбитным СНС относятся СНС отечественные СНС «Парус» и «Цикада» и подобная им американская СНС NNSS «Transit». Данные СНС построены на одних и тех же принципах и имеют одинаковую структуру. Несущественные различия есть в параметрах орбит, количестве НКА, организации траекторных измерений, математических методах прогнозирования и формах представления орбиты. Основные характеристики СНС «Парус», «Цикада» и «Transit» приведены в табл. 13.2.
| Параметр | «Парус» | «Цикада» | «Transit» |
| Зона действия | Без ограничений | Без ограничений | До широт ±88° |
| Номинальное количество НКА | 6 | 4 | 6 |
| Угол наклонения орбиты | 82,9° | 83° | 90° |
| Высота орбиты в апогее | 1017 км | 1024 км | 1075 км |
|
Диапазон рабочих частот Мгц |
149,91-150,03 399,76-400,08 |
150,00 400,00 |
149,988 399,968 |
| Геодезическая основа | Эллипсоид Красовского | Эллипсоид Красовского |
Эллипсоид WGS-72 |
| Шкала времени | Московское зимнее время | Московское зимнее время | Гринвичское время |
| СКП 100м | |||
Определение местоположения путём измерения расстояний до объекта от точек с известными координатами — спутников. Расстояние вычисляется по времени задержки распространения сигнала от посылки его спутником до приёма антенной GPS-приёмника. для определения 3d координат GPS-приёмнику нужно знать расстояние до трёх спутников и время GPS системы. благодаря эффекту Доплера частота принимаемого сигнала увеличивается при приближении спутника и уменьшается при его отдалении. точно зная положение спутника, можно определить собственную скорость и координаты.
42. Назначение, принцип действия, состав, основные ТТХ среднеорбитых СНС. Принцип получения навигационного параметра
Для высокоточного определения координат места и составляющих скорости наземных, морских, речных, воздушных и других подвижных объектов в любой точке земного шара. определение местоположения путём измерения расстояний до объекта от точек с известными координатами — спутников. Расстояние вычисляется по времени задержки распространения сигнала от посылки его спутником до приёма антенной GPS-приёмника. для определения 3d координат GPS-приёмнику нужно знать расстояние до трёх спутников и время GPS системы. благодаря эффекту Доплера частота принимаемого сигнала увеличивается при приближении спутника и уменьшается при его отдалении. точно зная положение спутника, можно определить собственную скорость и координаты.
Основное назначение среднеорбитной СНС второго поколения - глобальная оперативная навигация наземных, морских, воздушных и низкоорбитных космических подвижных объектов.
Система ГЛОНАСС разработана по заказу и находится под управлением Министерства Обороны РФ.
| Характеристики | ГЛОНАСС | GPS |
| Номинальное количество спутников в системе | 24 | 24 |
| Число орбитальных плос | 3 | 6 |
| Наклонение орбиты | 64,8° | 55° |
| Высота орбиты | 19100км | 20000км |
| Период обращения | 11ч 16м | 12ч |
| Метод представления эфемеридных | 9 параметров движения | Кепплеровские элементы |
| Геод система коорд | ПЗ-90 | WGS-84 |
| Содержимое альманаха | 120 бит | 152 бит |
|
Длит передачи альманаха Метод разделения сигналов НКА Диапазон частот L1 |
2,5м Частотный 1602,5625-1615,5 |
12,5м Кодовый 1575,41±1 МГц |
| Селективный доступ | Отсутствует | Имеется |
| Диапазон частот L2 | 1246,4375-1256,5 | 1227,6МГц |
43. Пространственная прямоугольная система координат. Взаимосвязь местоположения и скорости судна от расстояний до НИСЗ
В отличие от обычных астрономических обсерваций, где измеряются только направления на светила относительно оси вращения Земли и отвесной линии, при обсервациях по СНС учитываются закономерности изменения расстояния между спутниками и судном при их взаимном перемещении в пространстве. Поэтому при обсервациях по СНС применяют пространственную систему координат XYZ, участвующую во вращении Земли. Начало этой системы координат принимается в центре Земли О, ось X лежит в плоскости гринвичского меридиана, а ось Z направлена к северному полюсу мира. Для получения обсервованных координат места по наклонной дальности D или по скорости ее изменения Vd необходимо математически связать:
-
пространственные прямоугольные координаты НКАσ (х0, у0, z0) и проекции
вектора скорости ИСЗ ![]() σ (Vx, Vy, Vz);
σ (Vx, Vy, Vz);
-
пространственные прямоугольные координаты М (xм, ум, zм) и проекции вектора
скорости судна![]() (vx, vy, vz).
(vx, vy, vz).
Исходными данными при этом будут служить:
-
для НКА - геоцентрический радиус-вектор ![]() = Rσ
+ hп и скорость Vσ,
а
также эфемеридная информация II
вида, позволяющая вычислить значения направляющих косинусов углов ХОσ, YOσ,
ZOσ;
= Rσ
+ hп и скорость Vσ,
а
также эфемеридная информация II
вида, позволяющая вычислить значения направляющих косинусов углов ХОσ, YOσ,
ZOσ;
-
для судовой навигационной аппаратуры - геоцентрический радиус-вектор приемной
антенны ![]() =Rм
+
hант, где hант
-
высота антенны над уровнем моря; скорость V
и
путевой угол судна ПУ, геоцентрические координаты судна φ' и λ. Географическая
широта φ и геоцентрическая широта φ' связаны известным выражением:
φ = arctg [tg
φ' (1 - е2)-1] при наибольшей разнице φ - φ'=11,5' на широте
φ =45°.
=Rм
+
hант, где hант
-
высота антенны над уровнем моря; скорость V
и
путевой угол судна ПУ, геоцентрические координаты судна φ' и λ. Географическая
широта φ и геоцентрическая широта φ' связаны известным выражением:
φ = arctg [tg
φ' (1 - е2)-1] при наибольшей разнице φ - φ'=11,5' на широте
φ =45°.
44. Методы получения навигационных параметров, используемые в в СНС
Определение местоположения путём измерения расстояний до объекта от точек с известными координатами — спутников. Расстояние вычисляется по времени задержки распространения сигнала от посылки его спутником до приёма антенной GPS-приёмника. для определения 3d координат GPS-приёмнику нужно знать расстояние до трёх спутников и время GPS системы. благодаря эффекту Доплера частота принимаемого сигнала увеличивается при приближении спутника и уменьшается при его отдалении. точно зная положение спутника, можно определить собственную скорость и координаты.
Среднестатистические значения погрешностей измерения навигационных параметров среднеорбитных СНС.
| Составляющие погрешности | Псевдодальности (м) | Псевдоскорости (см/с) | ||
|
Грубый канал |
Точны канал |
Грубы канал |
Точны канал |
|
| Эфемеридная погрешность | 0,6-1,5 | 0,6-1,5 | - | - |
| Ионосферная погрешность | 5,0-20,0 | 0,01-0,05 | 5,0 | 0,01 |
| Тропосферная погрешность | 1,0-2,0 | 1,0-2,0 | 0,1 | 0,1 |
| Инструментальная погрешность | 1,0-1,2 | 0,35 | 20 | 20 |
|
Погрешность взаимной синхронизации определителей времени |
0,6-2,7 | 0,6-2,7 | - | - |
45. Получение места судна по измеренным азимутам светил
Азимутальная линия положения. Измеренному азимуту А соответствует на земном шаре изолиния РnМδ, называемая изоазимутой (рис. 6.7). Текущие координаты места судна М (φ, λ), координаты географического места светила σ (tгр, δ) и азимут А связывает уравнение изоазимуты:
ctg A = cos φ tg δ cosec tм - sin φ ctg tм. (6.11)
Малый отрезок изоазимуты в районе счислимого места С (рис. 6.8), совпадающий с прямой линией 1-1, является азимутальной линией положения (АЛП), уравнение которой имеет вид: cos τАΔ φ + sin τАΔω = (А-Ас)/gА, (6.12)
где - τА - угол, определяющий направление градиента азимута в счислимом месте; - Ас - счислимый азимут; - gA - модуль градиента азимута, выражающийся формулой:
![]() (6.13)
(6.13)
Для получения элементов АЛП необходимо 1. Измерить азимут светила и исправить его поправкой системы курсоуказания ΔK и инструментальной поправкой визирующего устройства s. Вычисляют Ас и hc Вычисляют элементы nА и τА азимутальной линии положения
46. Получение места судна по измеренным разностям азимутов светил. Разностно-азимутальная линии положения
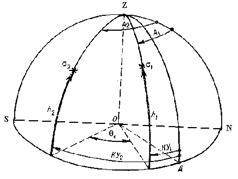
Разность азимутов двух светил может быть измерена непосредственно или найдена косвенным путем посредством измерения в один и тот же момент времени пеленгов или курсовых углов этих светил. При неодновременных измерениях пеленгов или КУ потребуется их приведение не только к одному месту, но и к одному моменту измерений, что может значительно осложнить решение. Разность азимутов ΔП=Θ, являясь астронавигационным параметром, обладает важным достоинством: в ней исключается погрешность поправки курсоуказания или погрешность установки измерительного устройства в диаметральной плоскости судна ОД (рис. 6.9), а также другие повторяющиеся погрешности измерений и исправления азимутов. Разность азимутов θ вычисляется по формуле:
Θ=А2 - А1=ИП2 - ИП1 , или Θ=КУ2 - КУ1. (6.20)
Разность азимутов Θ является углом на сфере между вертикалами светил, которому соответствует сферическая изогона - изолиния, аналогичная изоазимуте (рис. 6.7), если принять одно из светил находящимся над точкой Рn.
Разностно-азимутальная линия положения (РАЛП) является малым отрезком сферической изогоны в районе счислимого места С, принимаемым совпадающим с прямой линией (рис. 6.10). Элементы РАЛП nΘ и τΘ вычисляют по формулам:
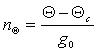 ;(6.21)
;(6.21)
 , (6.22)
, (6.22)
где Θс=Aс2 – Ас1 - счислимая разность азимутов в момет измерения азимутов (курсовых углов); gΘ - модуль градиента разности азимутов, определяемый графически (рис. 6.10) или по формуле:
![]() ,
,
47. Получение места судна по измеренным разностям высот светил. Разностно-высотная линии положения
Если в один и тот же момент времени были получены (рис. 6.9):
- для светила σ1 - высота h1 и азимут А1 (или КУ1),
- для светила σ2 - высота h2 и азимут А2 (или КУ2),
То задача определения обсервованных координат места судна в принципе сводится к отысканию точки пересечения сферической гиперболы I-I, отвечающей параметру h2-h1=Δh (разностно-высотной линии положения - РВЛП), и сферической изогоны II-II (разностно-азимутальной линии положения - РАЛП), отвечающей параметру Θ=А2-А1 (рис. 6.13). Практически решение выполняется одним из следующих методов:
1. Отыскивается точка пересечения М разностно-высотной линии положения (РВЛП) 1-1 и разностно-азимутальной линии положения (РАЛП) 2-2, как это показано на рис. 6.14. Элементами линий положениям соответственно являются:

 ,
,
Затем оценивается их точность и вычисляются веса обсервованных мест. С учетом этих весов находится вероятнейшее место, лежащее на прямой между исходными обсервованными точками.
48. Назначение, состав, принцип получения навигационных параметров в астронавигационной системе (АНС)
- Астронавигационные системы (АНС) - оптические, фотоэлектрические и телевизионные системы, предназначенные для автоматического измерения высот и азимутов (разности азимутов) оптически видимых небесных светил и слежения за ними.
Астронавигационная система (АНС) - это комплекс взаимосвязанных приборов и систем, предназначенных для автоматического или полуавтоматического измерения астронавигационных параметров (высот, азимутов, курсовых углов светил и скоростей их изменения) с целью автоматизированного определения обсервованных координат места и поправки курсоуказания. По принципу действия и построения эти системы можно подразделить на:
- оптические АНС, принимающие излучения светил в оптическом диапазоне частот;
- радиоастрономические навигационные системы (или радиосекстаны), принимающие сигналы естественных и искусственных источников космического радиоизлучения (ИКР);
- комбинированные системы, представляющие собой комбинацию первой и второй систем. Структурно-функциональная схема типовой комбинированной АНС без элементов гироскопической стабилизации изображена на рис. 12.11. Для наведения приемных устройств АНС, размещенных в головной части измерительного устройства ИУ на гиростабилизированной в плоскости истинного горизонта платформе ГСП, СЦВМ автоматически подбирает несколько групп светил (в том числе и ИСЗ) для наблюдений на заданные дату Д, всемирное время наблюдений Тгр и счислимые координаты места судна. Судоводителем с пульта задается избранное наименование светила (группы светил) или номер искусственного спутника Земли Nсв для наблюдений. Из системы автоматического счисления (навигационного комплекса или) в СЦВМ через аналоговое вычислительное устройство (АВУ) вводятся счислимые координаты места судна, его курс и скорость. По этим данным СЦВМ вычисляет углы наведения приемных устройств на светило или ИКР по высоте hн=hc, и по азимуту
qн = qc =Ac - КК,
Которые через АВУ поступают на приводы наведения по высоте и курсовому углу.
Приемным устройством для светового излучения является телескоп Тл, сопряженный с приемной телевизионной камерой или фотоэлементом, а для радиоизлучения - антенна Ант с остронаправленной диаграммой приема. Чтобы выделить слабое световое или космическое радиоизлучение объекта наблюдения на фоне атмосферного излучения и помех, производится модуляция принимаемого светового потока или радиосигнала. Световой поток прерывается полупрозрачным вращающимся диском, а радиосигнал модулируется сканированием (вращением) диаграммы направленности антенны. В результате модуляции принимаемого излучения образуется линия визирования телескопа и равносигнальное направление РНС антенны. Если эти линии точно направлены на светило или ИКР, то в фото (оптико-телевизионном) блоке или радиоприемном устройстве электрических сигналов рассогласования не возникает. При отклонении указанных линий от направления на светило или ИКР возникает сигнал рассогласования ер с частотой модуляции, фаза которого зависит от стороны, а амплитуда – от угла отклонения. Фазы сигналов рассогласования по высоте е h и курсовому углу е q отличаются друг от друга на p/2- или 90°. Это обстоятельство позволяет в фазовых дискриминаторах, куда дополнительно подаются сдвинутые по фазе на 90° опорные напряжения Uоп от модуляционных устройств, из общего сигнала рассогласования выделить электрические сигналы рассогласования по высоте еh и курсовому углу еq, пропорциональные ошибкам наведения приемных устройств на светило или ИКР. Блоки коррекции по этим сигналам вырабатывают поправки Dh и Dq к исчислимым горизонтным координатам светил. Поправки суммируются со исчислимыми высотой и курсовым углом и через приводы наведения корректируют положение приемных устройств до тех пор, пока сигнал рассогласования ер не станет равным нулю, т.е. пока линия визирования телескопа или ось РНС не будут направлены на светило или ИКР. Блоки считывания высоты и курсового угла автоматически снимут фактические высоту hпр и курсовой угол qпр светила или ИКР. Они исправляются инструментальными поправками Dhu и Dqu, вычисляемыми в блоках выработки поправок. Измеренные высота hизм =hпр+Dhи и курсовой угол qизм=qпр+Dqи светила или ИКР через АВУ поступают в СЦВМ, где высота автоматически исправляется поправкой за рефракцию или радиорефракцию и рассчитывается компасный пеленг
КП=Акр=qизм+КК.
СЦВМ автоматически вычисляет поправки к счислимым координатам Djо и Dlо, поправку курсоуказания DК, обсервованные координаты места jо и lо, эллиптическую и радиальную СКП обсервованного места Мо. После анализа и утверждения их судоводителем они с пульта управления передаются в систему автоматического счисления (навигационный комплекс или систему электронной картографии). В современных АНС, особенно если они сопряжены с высокоточными гироскопическими приборами и системами (гироазимутами - ГА, гировертикалями - ГВ, гирогоризонтами – ГГ, гироазимутгоризонтами - ГАГ, инерциальными навигационными системами - ИНС), вырабатывающими направление компасного меридиана и плоскость горизонта, могут быть реализованы практически все рассмотренные в главе 6 способы определения места судна - высотный, азимутальный, разностно-высотный, разностно-азимутальный, высотно-разностно-азимутальный, скоростно-высотный и скоростно-азимутальный и другие.

