Содержание
Введение
1. Классификация АЦП
2. Параллельные АЦП
3. Последовательно-параллельные АЦП
3.1 Многоступенчатые АЦП
3.2 Многотактные АЦП
3.3 Конвеерные АЦП
4. Последовательные АЦП
4.1 АЦП последовательного счета
4.2 АЦП последовательного приближения
4.3 Интегрирующие АЦП
4.3.1 АЦП многотактного интегрирования
4.3.2 Сигма-дельта АЦП
4.4 Преобразователи напряжение-частота
5. Параметры АЦП
5.1 Статистические параметры
5.2 Динамические параметры
5.3 Шумы АЦП
Список используемой литературы
Введение
Аналого-цифровые преобразователи (АЦП) являются устройствами, которые принимают входные аналоговые сигналы и генерируют соответствующие им цифровые сигналы, пригодные для обработки микропроцессорами и другими цифровыми устройствами.
Принципиально не исключена возможность непосредственного преобразования различных физических величин в цифровую форму, однако эту задачу удается решить лишь в редких случаях из-за сложности таких преобразователей. Поэтому в настоящее время наиболее рациональным признается способ преобразования различных по физической природе величин сначала в функционально связанные с ними электрические, а затем уже с помощью преобразователей напряжение-код - в цифровые. Именно эти преобразователи имеют обычно в виду, когда говорят об АЦП.
Процедура аналого-цифрового преобразования непрерывных сигналов, которую реализуют с помощью АЦП, представляет собой преобразование непрерывной функции времени U(t), описывающей исходный сигнал, в последовательность чисел {U'(tj )}, j=0,1,2,:, отнесенных к некоторым фиксированным моментам времени. Эту процедуру можно разделить на две самостоятельные операции. Первая из них называется дискретизацией и состоит в преобразовании непрерывной функции времени U(t) в непрерывную последовательность {U(tj )}. Вторая называется квантованием и состоит в преобразовании непрерывной последовательности в дискретную {U'(tj )}.
В основе дискретизации непрерывных сигналов лежит принципиальная возможность представления их в виде взвешенных сумм
где aj - некоторые коэффициенты или отсчеты, характеризующие исходный сигнал в дискретные моменты времени; fj (t) - набор элементарных функций, используемых при восстановлении сигнала по его отсчетам.
Наиболее распространенной формой дискретизации является равномерная, в основе которой лежит теорема отсчетов. Согласно этой теореме в качестве коэффициентов aj следует использовать мгновенные значения сигнала U(tj ) в дискретные моменты времени tj =jDt, а период дискретизации выбирать из условия
Dt=1/2Fm ,
где Fm - максимальная частота спектра преобразуемого сигнала. При этом выражение (1) переходит в известное выражение теоремы отсчетов
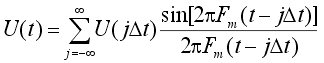
Для сигналов со строго ограниченным спектром это выражение является тождеством. Однако спектры реальных сигналов стремятся к нулю лишь асимптотически. Применение равномерной дискретизации к таким сигналам приводит к возникновению в системах обработки информации специфических высокочастотных искажений, обусловленных выборкой. Для уменьшения этих искажений необходимо либо увеличивать частоту дискретизации, либо использовать перед АЦП дополнительный фильтр нижних частот, ограничивающий спектр исходного сигнала перед его аналого-цифровым преобразованием.
В общем случае выбор частоты дискретизации будет зависеть также от используемого в (1) вида функции fj (t) и допустимого уровня погрешностей, возникающих при восстановлении исходного сигнала по его отсчетам. Все это следует принимать во внимание при выборе частоты дискретизации, которая определяет требуемое быстродействие АЦП. Часто этот параметр задают разработчику АЦП.
Рассмотрим более подробно место АЦП при выполнении операции дискретизации.
Для достаточно узкополосных сигналов операцию дискретизации можно выполнять с помощью самих АЦП и совмещать таким образом с операцией квантования. Основной закономерностью такой дискретизации является то, что за счет конечного времени одного преобразования и неопределенности момента его окончания, зависящего в общем случае от параметров входного сигнала, не удается получить однозначного соответствия между значениями отсчетов и моментами времени, к которым их следует отнести. В результате при работе с изменяющимися во времени сигналами возникают специфические погрешности, динамические по своей природе, для оценки которых вводят понятие апертурной неопределенности, характеризующейся обычно апертурным временем.
Апертурным временем ta называют время, в течение которого сохраняется неопределенность между значением выборки и временем, к которому она относится. Эффект апертурной неопределенности проявляется либо как погрешность мгновенного значения сигнала при заданных моментах измерения, либо как погрешность момента времени, в который производится измерение при заданном мгновенном значении сигнала. При равномерной дискретизации следствием апертурной неопределенности является возникновение амплитудных погрешностей, которые называются апертурными и численно равны приращению сигнала в течение апертурного времени.
Если использовать другую интерпретацию эффекта апертурной неопределенности, то ее наличие приводит к "дрожанию" истинных моментов времени, в которые берутся отсчеты сигнала, по отношению к равноотстоящим на оси времени моментам. В результате вместо равномерной дискретизации со строго постоянным периодом осуществляется дискретизация с флюктуирующим периодом повторения, что приводит к нарушению условий теоремы отсчетов и появлению уже рассмотренных апертурных погрешностей в системах цифровой обработки информации.
Такое значение апертурной погрешности можно определить, разложив выражение для исходного сигнала в ряд Тейлора в окрестностях точек отсчета, которое для j-й точки имеет вид
 |
и дает в первом приближении апертурную погрешность
где ta - апертурное время, которое для рассматриваемого случая является в первом приближении временем преобразования АЦП.
Обычно для оценки апертурных погрешностей используют синусоидальный испытательный сигнал U(t)=Um sinDt, для которого максимальное относительное значение апертурной погрешности
DUa /Um =Dta .
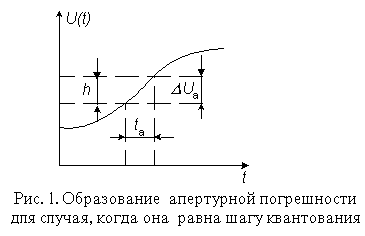
Если принять, что для N-разрядного АЦП с разрешением 2-N апертурная погрешность не должна превышать шага квантования (рис. 1), то между частотой сигнала D, апертурным временем ta и относительной апертурной погрешностью имеет место соотношение
1/2N =Dta .
Для обеспечения дискретизации синусоидального сигнала частотой 100 кГц с погрешностью 1% время преобразования АЦП должно быть равно 25 нс. В то же время с помощью такого быстродействующего АЦП принципиально можно дискретизировать сигналы, имеющие ширину спектра порядка 20 МГц. Таким образом, дискретизация с помощью самого АЦП приводит к существенному расхождению требований между быстродействием АЦП и периодом дискретизации. Это расхождение достигает 2...3 порядков и сильно усложняет и удорожает процесс дискретизации, так как даже для сравнительно узкополосных сигналов требует весьма быстродействующих АЦП. Для достаточно широкого класса быстро изменяющихся сигналов эту проблему решают с помощью устройств выборки-хранения, имеющих малое апертурное время.
1. Классификация
В настоящее время известно большое число методов преобразования напряжение-код. Эти методы существенно отличаются друг от друга потенциальной точностью, скоростью преобразования и сложностью аппаратной реализации. На рис. 2 представлена классификация АЦП по методам преобразования.
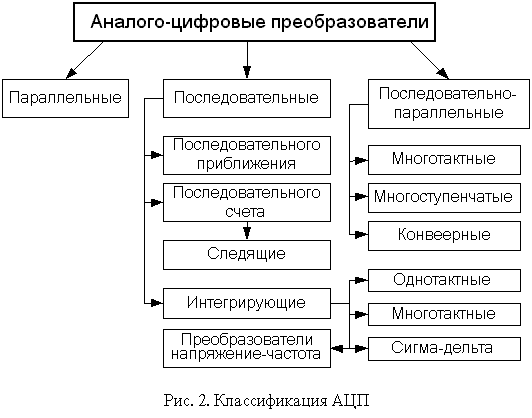 |
В основу классификации АЦП положен признак, указывающий на то, как во времени разворачивается процесс преобразования аналоговой величины в цифровую. В основе преобразования выборочных значений сигнала в цифровые эквиваленты лежат операции квантования и кодирования. Они могут осуществляться с помощью либо последовательной, либо параллельной, либо последовательно-параллельной процедур приближения цифрового эквивалента к преобразуемой величине.
2. Параллельные АЦП
 |
АЦП этого типа осуществляют квантование сигнала одновременно с помощью набора компараторов, включенных параллельно источнику входного сигнала. На рис. 3 показана реализация параллельного метода АЦ-преобразования для 3-разрядного числа.
С помощью трех двоичных разрядов можно представить восемь различных чисел, включая нуль. Необходимо, следовательно, семь компараторов. Семь соответствующих эквидистантных опорных напряжений образуются с помощью резистивного делителя.
Если приложенное входное напряжение не выходит за пределы диапазона от 5 /2 h, до 7 /2 h, где h=Uоп /7 - квант входного напряжения, соответствующий единице младшего разряда АЦП, то компараторы с 1-го по 3-й устанавливаются в состояние 1, а компараторы с 4-го по 7-й - в состояние 0. Преобразование этой группы кодов в трехзначное двоичное число выполняет логическое устройство, называемое приоритетным шифратором, диаграмма состояний которого приведена в табл.1.
Таблица 1
| Входное напряжение | Состояние компараторов | Выходы | ||||||||
| Uвх /h | К7 | К6 | К5 | К4 | К3 | К2 | К1 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 4 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 5 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Подключение приоритетного шифратора непосредственно к выходу АЦП может привести к ошибочному результату при считывании выходного кода. Рассмотрим, например переход от трех к четырем, или в двоичном коде от 011 к 100. Если старший разряд вследствие меньшего времени задержки изменит свое состояние раньше других разрядов, то временно на выходе возникнет число 111, т.е. семь. Величина ошибки в этом случае составит половину измеряемого диапазона.
Так как результаты АЦ-преобразования записываются, как правило, в запоминающее устройство, существует вероятность получить полностью неверную величину. Решить эту проблему можно, например, с помощью устройства выборки-хранения (УВХ). Некоторые интегральные микросхемы (ИМС) параллельных АЦП, например МАХ100, снабжаются сверхскоростными УВХ, имеющими время выборки порядка 0,1 нс. Другой путь состоит в использовании кода Грея, характерной особенностью которого является изменение только одной кодовой позиции при переходе от одного кодового значения к другому. Наконец, в некоторых АЦП (например, МАХ1151) для снижения вероятности сбоев при параллельном АЦ-преобразовании используется двухтактный цикл, когда сначала состояния выходов компараторов фиксируются, а затем, после установления состояния приоритетного шифратора, подачей активного фронта на синхровход выходного регистра в него записывают выходное слово АЦП.
Как видно из табл. 1, при увеличении входного сигнала компараторы устанавливаются в состояние 1 по очереди - снизу вверх. Такая очередность не гарантируется при быстром нарастании входного сигнала, так как из-за различия во временах задержки компараторы могут переключаться в другом порядке. Приоритетное кодирование позволяет избежать ошибки, возможной в этом случае, благодаря тому, что единицы в младших разрядах не принимаются во внимание приоритетным шифратором.
Благодаря одновременной работе компараторов параллельный АЦП является самым быстрым. Например, восьмиразрядный преобразователь типа МАХ104 позволяет получить 1 млрд отсчетов в секунду при времени задержки прохождения сигнала не более 1,2 нс. Недостатком этой схемы является высокая сложность. Действительно, N-разрядный параллельный АЦП сдержит 2N-1 компараторов и 2N согласованных резисторов. Следствием этого является высокая стоимость (сотни долларов США) и значительная потребляемая мощность. Тот же МАХ104, например, потребляет около 4 Вт.
3. Последовательно-параллельные АЦП
Последовательно-параллельные АЦП являются компромиссом между стремлением получить высокое быстродействие и желанием сделать это по возможности меньшей ценой. Последовательно-параллельные АЦП занимают промежуточное положение по разрешающей способности и быстродействию между параллельными АЦП и АЦП последовательного приближения. Последовательно-параллельные АЦП подразделяют на многоступенчатые, многотактные и конвеерные.
3.1 Многоступенчатые АЦП
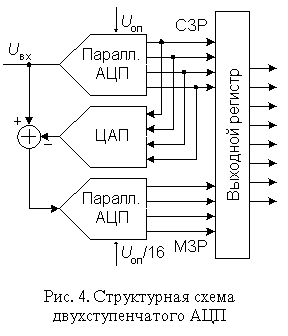 |
В многоступенчатом АЦП процесс преобразования входного сигнала разделен в пространстве. В качестве примера на рис. 4 представлена схема двухступенчатого 8-разрядного АЦП.
Верхний по схеме АЦП осуществляет грубое преобразование сигнала в четыре старших разряда выходного кода. Цифровые сигналы с выхода АЦП поступают на выходной регистр и одновременно на вход 4-разрядного быстродействующего ЦАП. Во многих ИМС многоступенчатых АЦП (AD9042, AD9070 и др.) этот ЦАП выполнен по схеме суммирования токов на дифференциальных переключателях, но некоторые (AD775, AD9040A и др.) содержат ЦАП с суммированием напряжений. Остаток от вычитания выходного напряжения ЦАП из входного напряжения схемы поступает на вход АЦП2, опорное напряжение которого в 16 раз меньше, чем у АЦП1. Как следствие, квант АЦП2 в 16 раз меньше кванта АЦП1. Этот остаток, преобразованный АЦП2 в цифровую форму представляет собой четыре младших разряда выходного кода. Различие между АЦП1 и АЦП2 заключается прежде всего в требовании к точности: у АЦП1 точность должна быть такой же как у 8-разрядного преобразователя, в то время как АЦП2 может иметь точность 4-разрядного.
Грубо приближенная и точная величины должны, естественно, соответствовать одному и тому же входному напряжению Uвх (tj ). Из-за наличия задержки сигнала в первой ступени возникает, однако, временнoе запаздывание. Поэтому при использовании этого способа входное напряжение необходимо поддерживать постоянным с помощью устройства выборки-хранения до тех пор, пока не будет получено все число.
3.2 Многотактные последовательно-параллельные АЦП
Рассмотрим пример 8-разрядного последовательно-параллельного АЦП, относящегося к типу многотактных (рис. 5). Здесь процесс преобразования разделен во времени.
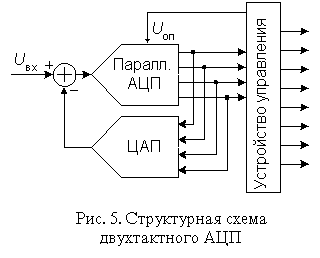
Преобразователь состоит из 4-разрядного параллельного АЦП, квант h которого определяется величиной опорного напряжения, 4-разрядного ЦАП и устройства управления. Если максимальный входной сигнал равен 2,56 В, то в первом такте преобразователь работает с шагом квантования h1 =0,16 В. В это время входной код ЦАП равен нулю. Устройство управления пересылает полученное от АЦП в первом такте слово в четыре старших разряда выходного регистра, подает это слово на вход ЦАП и уменьшает в 16 раз опорное напряжение АЦП. Таким образом, во втором такте шаг квантования h2 =0,01 В и остаток, образовавшийся при вычитании из входного напряжения схемы выходного напряжения ЦАП, будет преобразован в младший полубайт выходного слова.
Очевидно, что используемые в этой схеме 4-разрядные АЦП и ЦАП должны обладать 8-разрядной точностью, в противном случае возможен пропуск кодов, т.е. при монотонном нарастании входного напряжения выходной код АЦП не будет принимать некоторые значения из своей шкалы. Так же, как и в предыдущем преобразователе, входное напряжение многотактного АЦП во время преобразования должно быть неизменным, для чего между его входом и источником входного сигнала следует включить устройство выборки-хранения.
Быстродействие рассмотренного многотактного АЦП определяется полным временем преобразования 4-разрядного АЦП, временем срабатывания цифровых схем управления, временем установления ЦАП с погрешностью, не превышающей 0,2...0,3 кванта 8-разрядного АЦП, причем время преобразования АЦП входит в общее время преобразования дважды. В результате при прочих равных условиях преобразователь такого типа оказывается медленнее двухступенчатого преобразователя, рассмотренного выше. Однако он проще и дешевле. По быстродействию многотактные АЦП занимают промежуточное положение между многоступенчатыми АЦП и АЦП последовательного приближения. Примерами многотактных АЦП являются трехтактный 12-разрядный AD7886 со временем преобразования 1 мкс, или трехтактный 16-разрядный AD1382 со временем преобразования 2 мкс.
3.3 Конвеерные АЦП
Быстродействие многоступенчатого АЦП можно повысить, применив конвеерный принцип многоступенчатой обработки входного сигнала. В обыкновенном многоступенчатом АЦП (рис. 4) вначале происходит формирование старших разрядов выходного слова преобразователем АЦП1, а затем идет период установления выходного сигнала ЦАП. На этом интервале АЦП2 простаивает. На втором этапе во время преобразования остатка преобразователем АЦП2 простаивает АЦП1. Введя элементы задержки аналогового и цифрового сигналов между ступенями преобразователя, получим конвеерный АЦП, схема 8-разрядного варианта которого приведена на рис. 6.
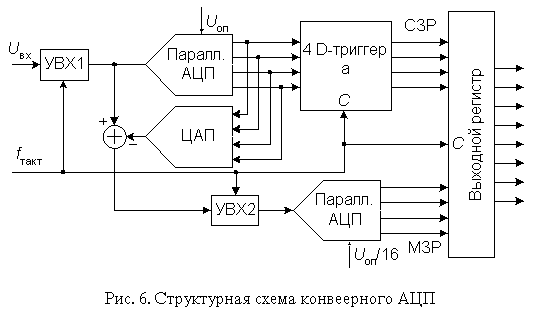
Роль аналогового элемента задержки выполняет устройство выборки-хранения УВХ2, а цифрового - четыре D-триггера. Триггеры задерживают передачу старшего полубайта в выходной регистр на один период тактового сигнала CLK.
Сигналы выборки, формируемые из тактового сигнала, поступают на УВХ1 и УВХ2 в разные моменты времени (рис. 7). УВХ2 переводится в режим хранения позже, чем УВХ1 на время, равное суммарной задержке распространения сигнала по АЦП1 и ЦАП. Задний фронт тактового сигнала управляет записью кодов в D-триггеры и выходной регистр. Полная обработка входного сигнала занимает около двух периодов CLK, но частота появления новых значений выходного кода равна частоте тактового сигнала.
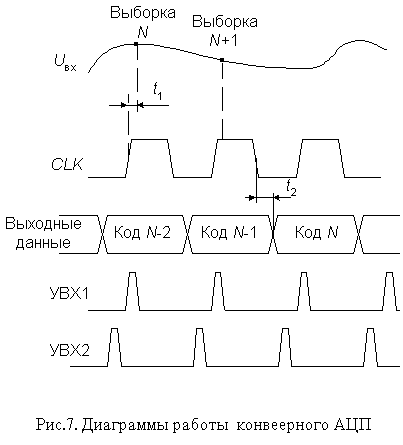
Таким образом, конвеерная архитектура позволяет существенно (в несколько раз) повысить максимальную частоту выборок многоступенчатого АЦП. То, что при этом сохраняется суммарная задержка прохождения сигнала, соответствующая обычному многоступенчатому АЦП с равным числом ступеней, не имеет существенного значения, так как время последующей цифровой обработки этих сигналов все равно многократно превосходит эту задержку. За счет этого можно без проигрыша в быстродействии увеличить число ступеней АЦП, понизив разрядность каждой ступени. В свою очередь, увеличение числа ступеней преобразования уменьшает сложность АЦП. Действительно, например, для построения 12-разрядного АЦП из четырех 3-разрядных необходимо 28 компараторов, тогда как его реализация из двух 6-разрядных потребует 126 компараторов.
Конвеерную архитектуру имеет большое количество выпускаемых в настоящее время многоступенчатых АЦП. В частности, 2-ступенчатый 10-разрядный AD9040А, выполняющий до 40 млн. преобразований в секунду (МПс), 4-ступенчатый 12-разрядный AD9220 (10 МПс), потребляющий всего 250 мВт, и др. При выборе конвеерного АЦП следует иметь в виду, что многие из них не допускают работу с низкой частотой выборок. Например, изготовитель не рекомендует работу ИМС AD9040А с частотой преобразований менее 10 МПс, 3-ступенчатого 12-разрядного AD9022 с частотой менее 2 МПс и т.д. Это вызвано тем, что внутренние УВХ имеют довольно высокую скорость разряда конденсаторов хранения, поэтому работа с большим тактовым периодом приводит к значительному изменению преобразуемого сигнала в ходе преобразования.
4. Последовательные АЦП
4.1 АЦП последовательного счета
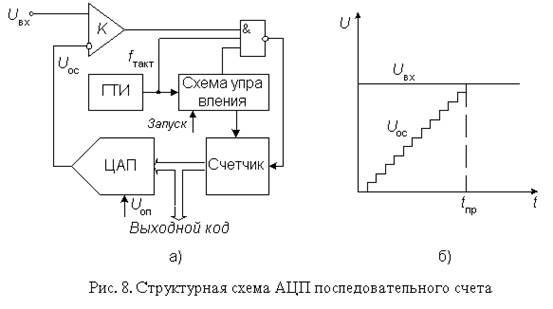 |
Этот преобразователь является типичным примером последовательных АЦП с единичными приближениями и состоит из компаратора, счетчика и ЦАП (рис. 8). На один вход компаратора поступает входной сигнал, а на другой - сигнал обратной связи с ЦАП.
Работа преобразователя начинается с прихода импульса запуска, который включает счетчик, суммирующий число импульсов, поступающих от генератора тактовых импульсов ГТИ. Выходной код счетчика подается на ЦАП, осуществляющий его преобразование в напряжение обратной связи Uос . Процесс преобразования продолжается до тех пор, пока напряжение обратной связи сравняется со входным напряжением и переключится компаратор, который своим выходным сигналом прекратит поступление тактовых импульсов на счетчик. Переход выхода компаратора из 1 в 0 означает завершение процесса преобразования. Выходной код, пропорциональный входному напряжению в момент окончания преобразования, считывается с выхода счетчика.
Время преобразования АЦП этого типа является переменным и определяется входным напряжением. Его максимальное значение соответствует максимальному входному напряжению и при разрядности двоичного счетчика N и частоте тактовых импульсов fтакт равно
tпр.макс =(2N -1)/ fтакт.
Например, при N=10 и fтакт =1 МГц tпр.макс =1024 мкс, что обеспечивает максимальную частоту выборок порядка 1 кГц.
Статическая погрешность преобразования определяется суммарной статической погрешностью используемых ЦАП и компаратора. Частоту счетных импульсов необходимо выбирать с учетом завершения переходных процессов в них.
При работе без устройства выборки-хранения апертурное время совпадает с временем преобразования. Как следствие, результат преобразования черезвычайно сильно зависит от пульсаций входного напряжения. При наличии высокочастотных пульсаций среднее значение выходного кода нелинейно зависит от среднего значения входного напряжения. Это означает, что АЦП данного типа без устройства выборки-хранения пригодны для работы с постоянными или медленно изменяющимися напряжениями, которые за время преобразования изменяются не более, чем на значение кванта преобразования.
Таким образом, особенностью АЦП последовательного счета является небольшая частота дискретизации, достигающая нескольких килогерц. Достоинством АЦП данного класса является сравнительная простота построения, определяемая последовательным характером выполнения процесса преобразования.
4.2 АЦП последовательного приближения
Преобразователь этого типа, называемый в литературе также АЦП с поразрядным уравновешиванием, является наиболее распространенным вариантом последовательных АЦП.
В основе работы этого класса преобразователей лежит принцип дихотомии, т.е последовательного сравнения измеряемой величины с 1 /2 , 1 /4 , 1 /8 и т.д. от возможного максимального значения ее. Это позволяет для N-разрядного АЦП последовательного приближения выполнить весь процесс преобразования за N последовательных шагов (итераций) вместо 2N -1 при использовании последовательного счета и получить существенный выигрыш в быстродействии. Так, уже при N=10 этот выигрыш достигает 100 раз и позволяет получить с помощью таких АЦП до 105 ...106 преобразований в секунду. В то же время статическая погрешность этого типа преобразователей, определяемая в основном используемым в нем ЦАП, может быть очень малой, что позволяет реализовать разрешающую способность до 18 двоичных разрядов при частоте выборок до 200 кГц (например, DSP101 фирмы Burr-Brown).
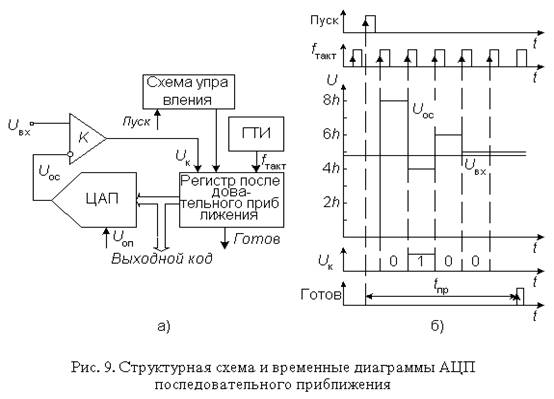 |
Рассмотрим принципы построения и работы АЦП последовательного приближения на примере классической структуры (рис. 9а) 4-разрядного преобразователя, состоящего из трех основных узлов: компаратора, регистра последовательного приближения (РПП) и ЦАП.
После подачи команды "Пуск" с приходом первого тактового импульса РПП принудительно задает на вход ЦАП код, равный половине его шкалы (для 4-разрядного ЦАП это 10002 =810 ). Благодаря этому напряжение Uос на выходе ЦАП (рис. 9б)
Uос =23 h.
где h - квант выходного напряжения ЦАП, соответствующий единице младшего разряда (ЕМР). Эта величина составляет половину возможного диапазона преобразуемых сигналов. Если входное напряжение больше, чем эта величина, то на выходе компаратора устанавливается 1, если меньше, то 0.
В этом последнем случае схема управления должна переключить старший разряд d3 обратно в состояние нуля. Непосредственно вслед за этим остаток
Uвх - d3 23 h
таким же образом сравнивается с ближайшим младшим разрядом и т.д. После четырех подобных выравнивающих шагов в регистре последовательного приближения оказывается двоичное число, из которого после цифро-аналогового преобразования получается напряжение, соответствующее Uвх с точностью до 1 ЕМР. Выходное число может быть считано с РПП в виде параллельного двоичного кода по N линиям. Кроме того, в процессе преобразования на выходе компаратора, как это видно из рис. 9б, формируется выходное число в виде последовательного кода старшими разрядами вперед.
Быстродействие АЦП данного типа определяется суммой времени установления tуст ЦАП до установившегося значения с погрешностью, не превышающей 0,5 ЕМР, времени переключения компаратора tк и задержки распространения сигнала в регистре последовательного приближения tз . Сумма tк + tз является величиной постоянной, а tуст уменьшается с уменьшением веса разряда. Следовательно для определения младших разрядов может быть использована более высокая тактовая частота. При поразрядной вариации fтакт возможно уменьшение времени преобразования tпр на 40%. Для этого в состав АЦП может быть включен контроллер.
При работе без устройства выборки-хранения апертурное время равно времени между началом и фактическим окончанием преобразования, которое так же, как и у АЦП последовательного счета, по сути зависит от входного сигнала, т.е. является переменным. Возникающие при этом апертурные погрешности носят также нелинейный характер. Поэтому для эффективного использования АЦП последовательного приближения, между его входом и источником преобразуемого сигнала следует включать УВХ. Большинство выпускаемых в настоящее время ИМС АЦП последовательного приближения (например, 12-разрядный МАХ191, 16-разрядный AD7882 и др.), имеет встроенные устройства выборки-хранения или, чаще, устройства слежения-хранения (track-hold), управляемые сигналом запуска АЦП. Устройство слежения-хранения отличается тем, что постоянно находится в режиме выборки, переходя в режим хранения только на время преобразования сигнала.
Данный класс АЦП занимает промежуточное положение по быстродействию, стоимости и разрешающей способности между последовательно-параллельными и интегрирующими АЦП и находит широкое применение в системах управления, контроля и цифровой обработки сигналов.
4.3 Интегрирующие АЦП
Недостатком рассмотренных выше последовательных АЦП является низкая помехоустойчивость результатов преобразования. Действительно, выборка мгновенного значения входного напряжения, обычно включает слагаемое в виде мгновенного значения помехи. Впоследствии при цифровой обработке последовательности выборок эта составляющая может быть подавлена, однако на это требуется время и вычислительные ресурсы. В АЦП, рассмотренных ниже, входной сигнал интегрируется либо непрерывно, либо на определенном временнoм интервале, длительность которого обычно выбирается кратной периоду помехи. Это позволяет во многих случаях подавить помеху еще на этапе преобразования. Платой за это является пониженное быстродействие интегрирующих АЦП.
4.3.1 АЦП многотактного интегрирования
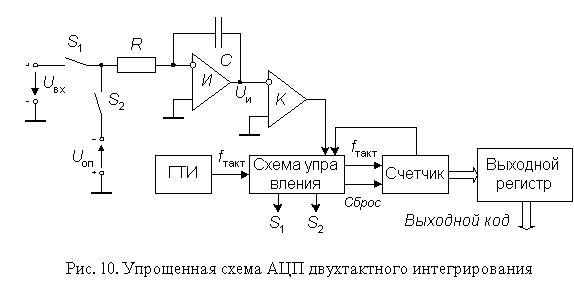 |
Упрощенная схема АЦП, работающего в два основных такта (АЦП двухтактного интегрирования), приведена на рис. 10.
Преобразование проходит две стадии: стадию интегрирования и стадию счета. В начале первой стадии ключ S1 замкнут, а ключ S2 разомкнут. Интегратор И интегрирует входное напряжение Uвх . Время интегрирования входного напряжения t1 постоянно; в качестве таймера используется счетчик с коэффициентом пересчета Kсч , так что
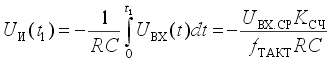 |
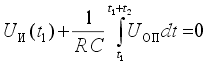 |
К моменту окончания интегрирования выходное напряжение интегратора составляет (7)
где Uвх.ср. - среднее за время t1 входное напряжение. После окончания стадии интегрирования ключ S1 размыкается, а ключ S2 замыкается и опорное напряжение Uоп поступает на вход интегратора. При этом выбирается опорное напряжение, противоположное по знаку входному напряжению. На стадии счета выходное напряжение интегратора линейно
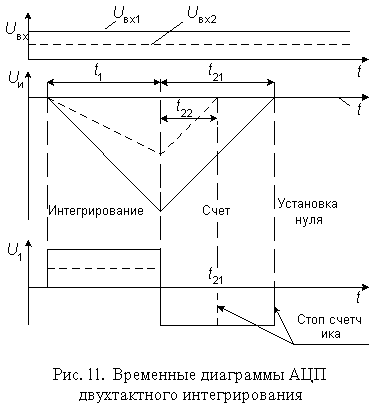 |
уменьшается по абсолютной величине, как показано на рис. 11.
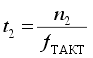 |
Стадия счета заканчивается, когда выходное напряжение интегратора переходит через нуль. При этом компаратор К переключается и счет останавливается. Интервал времени, в котором проходит стадия счета, определяется уравнением
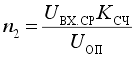 |
Подставив значение Uи (t1 ) из (7) в (8) с учетом того, что (9)
где n2 - содержимое счетчика после окончания стадии счета, получим результат (10)
Из этой формулы следует, что отличительной особенностью метода многотактного интегрирования является то, что ни тактовая частота, ни постоянная интегрирования RC не влияют на результат. Необходимо только потребовать, чтобы тактовая частота в течение времени t1 +t2 оставалась постоянной. Это можно обеспечить при использовании простого тактового генератора, поскольку существенные временные или температурные дрейфы частоты происходят за время несопоставимо большее, чем время преобразования.
При выводе выражений (6)...(10) мы видели, что в окончательный результат входят не мгновенные значения преобразуемого напряжения, а только значения, усредненные за время t1 . Поэтому переменное напряжение ослабляется тем сильнее, чем выше его частота.
Определим коэффициент передачи помехи Кп для АЦП двухтактного интегрирования. Пусть на вход интегратора поступает гармонический сигнал единичной амплитуды частотой f с произвольной начальной фазой j. Среднее значение этого сигнала за время интегрирования t1 равно (11)
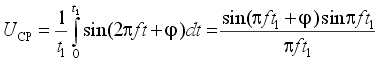 |
Эта величина достигает максимума по модулю при = +/- k, k=0, 1,
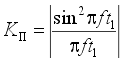 |
 |
2,... В этом случае (12)
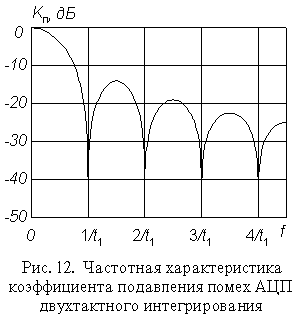
Из (12) следует, что переменное напряжение, период которого в целое число раз меньше t1 , подавляется совершенно (рис. 12). Поэтому целесообразно выбрать тактовую частоту такой, чтобы произведение Kсч fтакт было бы равным, или кратным периоду напряжения промышленной сети.
4.3.2 Сигма-дельта АЦП
АЦП многотактного интегрирования имеют ряд недостатков. Во-первых, нелинейность переходной статической характеристики операционного усилителя, на котором выполняют интегратор, заметным образом сказывается на интегральной нелинейности характеристики преобразования АЦП высокого разрешения. Для уменьшения влияния этого фактора АЦП изготавливают многотактными. Например, 13-разрядный AD7550 выполняет преобразование в четыре такта. Другим недостатком этих АЦП является то обстоятельство, что интегрирование входного сигнала занимает в цикле преобразования только приблизительно третью часть. Две трети цикла преобразователь не принимает входной сигнал. Это ухудшает помехоподавляющие свойства интегрирующего АЦП. В-третьих, АЦП многотактного интегрирования должен быть снабжен довольно большим количеством внешних резисторов и конденсаторов с высококачественным диэлектриком, что значительно увеличивает место, занимаемое преобразователем на плате и, как следствие, усиливает влияние помех.
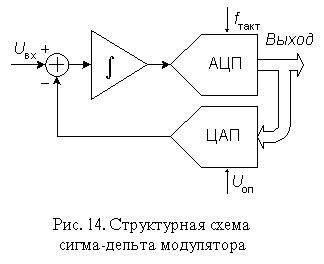 |
Эти недостатки во многом устранены в конструкции сигма-дельта АЦП (в ранней литературе эти преобразователи назывались АЦП с уравновешиванием или балансом зарядов). Своим названием эти преобразователи обязаны наличием в них двух блоков: сумматора (обозначение операции - ) и интегратора (обозначение операции - ). Один из принципов, заложенных в такого рода преобразователях, позволяющий уменьшить погрешность, вносимую шумами, а следовательно увеличить разрешающую способность - это усреднение результатов измерения на большом интервале времени.
Основные узлы АЦП - это сигма-дельта модулятор и цифровой фильтр. Схема n-разрядного сигма-дельта модулятора первого порядка приведена на рис. 14. Работа этой схемы основана на вычитании из входного сигнала Uвх (t) величины сигнала на выходе ЦАП, полученной на предыдущем такте работы схемы. Полученная разность интегрируется, а затем преобразуется в код параллельным АЦП невысокой разрядности. Последовательность кодов поступает на цифровой фильтр нижних частот.
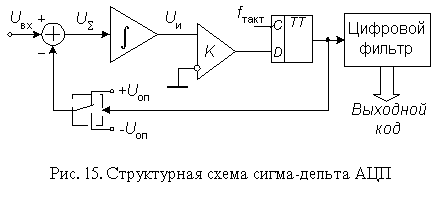
Порядок модулятора определяется численностью интеграторов и сумматоров в его схеме. Сигма-дельта модуляторы N-го порядка содержат N сумматоров и N интеграторов и обеспечивают большее соотношение сигнал/шум при той же частоте отсчетов, чем модуляторы первого порядка. Примерами сигма-дельта модуляторов высокого порядка являются одноканальный AD7720 седьмого порядка и двухканальный ADMOD79 пятого порядка.
Наиболее широко в составе ИМС используются однобитные сигма-дельта модуляторы, в которых в качестве АЦП используется компаратор, а в качестве ЦАП - аналоговый комутатор (рис. 15). Принцип действия пояснен в табл. 2 на примере преобразования входного сигнала, равного 0,6 В, при Uоп =1 В. Пусть постоянная времени интегрирования интегратора численно равна периоду тактовых импульсов. В нулевом периоде выходное напряжение интегратора сбрасывается в нуль. На выходе ЦАП также устанавливается нулевое напряжение. Затем схема проходит через показанную в табл. 9 последовательность состояний.
Таблица 2
| Uвх =0,6 В | Uвх =0 В | ||||||||
| N такта | U , В | Uи , В | Uк , бит | UЦАП , В | N такта | U , В | Uи , В | Uк , бит | UЦАП , В |
| 1 | 0,6 | 0,6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | -0,4 | 0,2 | 1 | 1 | 2 | -1 | 0 | 0 | -1 |
| 3 | -0,4 | -0,2 | 0 | -1 | 3 | 1 | 1 | 1 | 1 |
| 4 | 1,6 | 1,4 | 1 | 1 | 4 | -1 | 0 | 0 | -1 |
| 5 | -0,4 | 1,0 | 1 | 1 | 5 | 1 | 1 | 1 | 1 |
| 6 | -0,4 | 0,6 | 1 | 1 | 6 | -1 | 0 | 0 | -1 |
| 7 | -0,4 | 0,2 | 1 | 1 | 7 | 1 | 1 | 1 | 1 |
| 8 | -0,4 | -0,2 | 0 | -1 | 8 | -1 | 0 | 0 | -1 |
| 9 | 1,6 | 1,4 | 1 | 1 | 9 | 1 | 1 | 1 | 1 |
| 10 | -0,4 | 1,0 | 1 | 1 | 10 | -1 | 0 | 0 | -1 |
| 11 | -0,4 | 0,6 | 1 | 1 | 11 | 1 | 1 | 1 | 1 |
| 12 | -0,4 | 0,2 | 1 | 1 | 12 | -1 | 0 | 0 | -1 |
| 13 | -0,4 | -0,2 | 0 | -1 | 13 | 1 | 1 | 1 | 1 |
| 14 | 1,6 | 1,4 | 1 | 1 | 14 | -1 | 0 | 0 | -1 |
| 15 | -0,4 | 1,0 | 1 | 1 | 15 | 1 | 1 | 1 | 1 |
| 16 | -0,4 | 0,6 | 1 | 1 | 16 | -1 | 0 | 0 | -1 |
В тактовые периоды 2 и 7 состояния системы идентичны, так как при неизменном входном сигнале Uвх =0,6 В цикл работы занимает пять тактовых периодов. Усреднение выходного сигнала ЦАП за цикл действительно дает величину напряжения 0,6 В:
(1-1+1+1+1)/5=0,6.
Для формирования выходного кода такого преобразователя необходимо каким-либо образом преобразовать последовательность бит на выходе компаратора в виде унитарного кода в последовательный или параллельный двоичный позиционный код. В простейшем случае это можно сделать с помощью двоичного счетчика. Возьмем в нашем примере 4-разрядный счетчик. Подсчет бит на выходе компаратора за 16-ти тактный цикл дает число 13. Несложно увидеть, что при Uвх =1 В на выходе компаратора всегда будет единица, что дает за цикл число 16, т.е. переполнение счетчика. Напротив, при Uвх =-1 В на выходе компаратора всегда будет нуль, что дает равное нулю содержимое счетчика в конце цикла. В случае, если Uвх =0 то, как это видно из табл. 2, результат счета за цикл составит 810 или 10002 . Это значит, что выходное число АЦП представляется в смещенном коде. В рассмотренном примере верхняя граница полной шкалы составит 11112 или +710 , а нижняя - 00002 или -810 . При Uвх =0,6 В, как это видно из левой половины табл. 2, содержимое счетчика составит 1310 в смещенном коде, что соответствует +5. Учитывая, что +8 соответствует Uвх =1 В, найдем
5*1/8=0,625 > 0,6 В.
При использовании двоичного счетчика в качестве преобразователя потока битов, поступающих с выхода компаратора, необходимо выделять фиксированный цикл преобразования, длительность которого равна произведению Kсч fтакт . После его окончания должно производиться считывание результата, например, с помощью регистра-защелки и обнуление счетчика. В этом случае с точки зрения помехоподавляющих свойств сигма-дельта АЦП близки к АЦП многотактного интегрирования. Более эффективно с этой точки зрения применение в сигма-дельта АЦП цифровых фильтров с конечной длительностью переходных процессов.
В сигма-дельта АЦП обычно применяются цифровые фильтры с амплитудно-частотной характеристикой (АЧХ) вида (sinx/x)3 . Передаточная функция такого фильтра в z-области определяется выражением
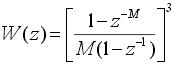
где М - целое число, которое задается программно и равно отношению тактовой частоты модулятора к частоте отсчетов фильтра. (Частота отсчетов - это частота, с которой обновляются данные).Например, для АЦП AD7714
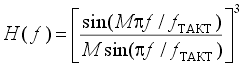 |
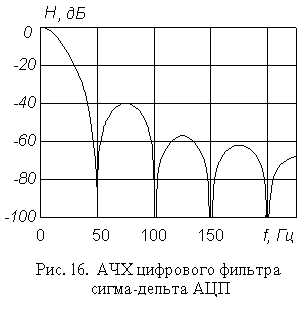
это число может принимать значения от 19 до 4000. В частотной области модуль передаточной функции фильтра (13) На рис. 16 приведен график амплитудно-частотной характеристики цифрового фильтра, построенной согласно выражению (13) при fтакт =38,4 кГц и М=192, что дает значение частоты отсчетов, совпадающей с первой частотой режекции фильтра АЦП, fотсч =50 Гц. Сравнение этой АЧХ с АЧХ коэффициента подавления помех АЦП с двухкратным интегрированием (см. рис. 12) показывает значительно лучшие помехоподавляющие свойства сигма-дельта АЦП.
В то же время применение цифрового фильтра нижних частот в составе сигма-дельта АЦП вместо счетчика вызывает переходные процессы при изменении входного напряжения. Время установления цифровых фильтров с конечной длительностью переходных процессов, как следует из их названия, конечно и составляет для фильтра вида (sinx/x)3 четыре периода частоты отсчетов, а при начальном обнулении фильтра - три периода. Это снижает быстродействие систем сбора данных на основе сигма-дельта АЦП. Поэтому выпускаются ИМС AD7730 и AD7731, оснащенные сложным цифровым фильтром, обеспечивающие переключение каналов со временем установления 1 мс при сохранении эффективной разрядности не ниже 13 бит (так называемый Fast-Step режим). Обычно цифровой фильтр изготавливается на том же кристалле, что и модулятор, но иногда они выпускаются в виде двух отдельных ИМС (например, AD1555 - модулятор
 |
четвертого порядка и AD1556 - цифровой фильтр).
Сравнение сигма-дельта АЦП с АЦП многотактного интегрирования показывает значительные преимущества первых. Прежде всего, линейность характеристики преобразования сигма-дельта АЦП выше, чем у АЦП многотактного интегрирования равной стоимости. Это объясняется тем, что интегратор сигма-дельта АЦП работает в значительно более узком динамическом диапазоне, и нелинейность переходной характеристики усилителя, на котором построен интегратор, сказывается значительно меньше. Емкость конденсатора интегратора у сигма-дельта АЦП значительно меньше (десятки пикофарад), так что этот конденсатор может быть изготовлен прямо на кристалле ИМС. Как следствие, сигма-дельта АЦП практически не имеет внешних элементов, что существенно сокращает площадь, занимаемую им на плате, и снижает уровень шумов. В результате, например, 24-разрядный сигма-дельта АЦП AD7714 изготавливается в виде однокристалльной ИМС в 24-выводном корпусе, потребляет 3 мВт мощности и стоит примерно 14 долларов США, а 18-разрядный АЦП восьмитактного интегрирования HI-7159 потребляет 75 мВт и стоит около 30 долларов. К тому же сигма-дельта АЦП начинает давать правильный результат через 3-4 отсчета после скачкообразного изменения входного сигнала, что при величине первой частоты режекции, равной 50 Гц, и 20-разрядном разрешении составляет 60-80 мс, а минимальное время преобразования АЦП HI-7159 для 18-разрядного разрешения и той же частоты режекции составляет 140 мс. В настоящее время ряд ведущих по аналого-цифровым ИМС фирм, такие как Analog Devices и Burr-Brown, прекратили производство АЦП многотактного интегрирования, полностью перейдя в области АЦ-преобразования высокого разрешения на сигма-дельта АЦП.
Сигма-дельта АЦП высокого разрешения имеют развитую цифровую часть, включающую микроконтроллер. Это позволяет реализовать режимы автоматической установки нуля и самокалибровки полной шкалы, хранить калибровочные коэффициенты и передавать их по запросу внешнего процессора.
4.4 Преобразователи напряжение-частота
На базе преобразователей напряжение-частота (ПНЧ) могут быть построены интегрирующие АЦП, обеспечивающие относительно высокую точность преобразования при низкой стоимости. Существует несколько видов ПНЧ. Наибольшее применение нашли ПНЧ с заданной длительностью выходного импульса. Структурная схема такого ПНЧ приведена на рис. 17. По этой схеме построена ИМС VFC-32 (отечественный аналог - 1108ПП1).
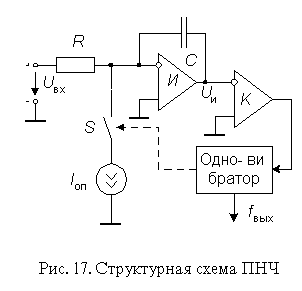 |
Работает ПНЧ следующим образом. Под действием положительного входного сигнала Uвх напряжение Uи на выходе интегратора И уменьшается. При этом ключ S разомкнут. Когда напряжение Uи уменьшится до нуля, компаратор К переключается, запуская тем самым одновибратор. Одновибратор формирует импульс стабильной длительности Ти , который управляет ключем. Последовательность этих импульсов является выходным сигналом ПНЧ. Ключ замыкается и ток Iоп в течение Ти поступает на вход интегратора, вызывая увеличение выходного напряжения интегратора. Далее описанный процесс снова повторяется.
Импульсы тока Iоп уравновешивают ток, вызываемый входным напряжением Uвх . В установившемся режиме
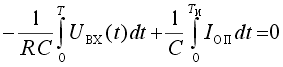 |
Отсюда следует
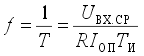 |
 |
где Uвх.ср - среднее значение входного напряжения за период Т. Выражение (14) показывает, что точность преобразования определяется точностью установки опорного тока Iоп , точностью выдержки длительности импульса одновибратора Ти, а также точностью резистора R. Емкость конденсатора интегратора не оказывает влияния на частоту ПНЧ.
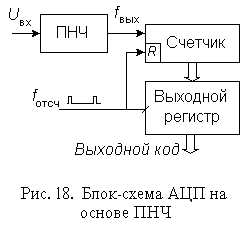
Таким образом, по существу ПНЧ преобразует входное напряжение в унитарный код. Для его преобразования в двоичный позиционный можно использовать счетчик. Схема интегрирующего АЦП на базе ПНЧ приведена на рис. 18. Двоичный счетчик подсчитывает число импульсов, поступивших от ПНЧ за период Тотсч =1/fотсч , задаваемый отсчетными импульсами, которыми содержимое счетчика заносится в выходной регистр-защелку. Вслед за этим происходит обнуление счетчика. Число импульсов n, подсчитанных счетчиком за время Тотсч ,
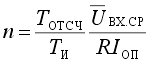 |
Здесь Uвх.ср - среднее значение входного напряжения за весь период Тотсч .
Можно заметно повысить точность ПНЧ, если вместо одновибратора включить тактируемый импульсами стабильной частоты D-триггер. Несложно убедиться (см. рис. 16), что в этом случае ПНЧ превращается в однобитный сигма-дельта модулятор.
5. Параметры АЦП
 |
|
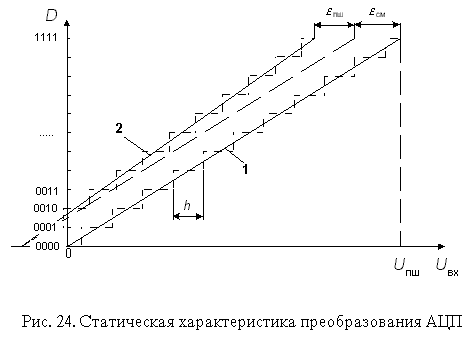
Такую зависимость по аналогии с ЦАП называют обычно характеристикой преобразования АЦП. В отсутствие аппаратных погрешностей средние точки ступенек расположены на идеальной прямой 1 (рис. 19), которой соответствует идеальная характеристика преобразования. Реальная характеристика преобразования может существенно отличаться от идеальной размерами и формой ступенек, а также расположением на плоскости координат. Для количественного описания этих различий существует целый ряд параметров.
5.1 Статические параметры
Разрешающая способность - величина, обратная максимальному числу кодовых комбинаций на выходе АЦП. Разрешающая способность выражается в процентах, разрядах или децибелах и характеризует потенциальные возможности АЦП с точки зрения достижимой точности. Например, 12-разрядный АЦП имеет разрешающую способность 1/4096, или 0,0245% от полной шкалы, или -72,2 дБ.
Разрешающей способности соответствует приращение входного напряжения АЦП Uвх при изменении Dj на единицу младшего разряда (ЕМР). Это приращение является шагом квантования. Для двоичных кодов преобразования номинальное значение шага квантования h=Uпш /(2N -1), где Uпш - номинальное максимальное входное напряжение АЦП (напряжение полной шкалы), соответствующее максимальному значению выходного кода, N - разрядность АЦП. Чем больше разрядность преобразователя, тем выше его разрешающая способность.
Погрешность полной шкалы - относительная разность между реальным и идеальным значениями предела шкалы преобразования при отсутствии смещения нуля.
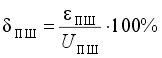 |
Эта погрешность является мультипликативной составляющей полной погрешности. Иногда указывается соответствующим числом ЕМР.
Погрешность смещения нуля - значение Uвх, когда входной код ЦАП равен нулю. Является аддитивной составляющей полной погрешности.
Обычно определяется по формуле
где Uвх.01 - значение входного напряжения, при котором происходит переход выходного кода из О в 1. Часто указывается в милливольтах или в процентах от полной шкалы:
![]()
Погрешности полной шкалы и смещения нуля АЦП могут быть уменьшены либо подстройкой аналоговой части схемы, либо коррекцией вычислительного алгоритма цифровой части устройства.
Погрешности линейности характеристики преобразования не могут быть устранены такими простыми средствами, поэтому они являются важнейшими метрологическими характеристиками АЦП.
Нелинейность - максимальное отклонение реальной характеристики преобразования D(Uвх ) от оптимальной (линия 2 на рис. 19). Оптимальная характеристика находится эмпирически так, чтобы минимизировать значение погрешности нелинейности. Нелинейность обычно определяется в относительных единицах, но в справочных данных приводится также и в ЕМР. Для характеристики, приведенной на рис. 25
Дифференциальной нелинейностью АЦП в данной точке k характеристики преобразования называется разность между значением кванта преобразования hk и средним значением кванта преобразования h. В спецификациях на конкретные АЦП значения дифференциальной нелинейности выражаются в долях ЕМР или процентах от полной шкалы.
Для характеристики, приведенной на рис. 25,
Погрешность дифференциальной линейности определяет два важных свойства АЦП: непропадание кодов и монотонность характеристики преобразования. Непропадание кодов - свойство АЦП выдавать все возможные выходные коды при изменении входного напряжения от начальной до конечной точки диапазона преобразования. Пример пропадания кода i+1 приведен на рис. 25. При нормировании непропадания кодов указывается эквивалентная разрядность АЦП - максимальное количество разрядов АЦП, для которых не пропадают соответствующие им кодовые комбинации.
Монотонность характеристики преобразования - это неизменность знака приращения выходного кода D при монотонном изменении входного преобразуемого сигнала. Монотонность не гарантирует малых значений дифференциальной нелинейности и непропадания кодов.
Температурная нестабильность АЦ-преобразователя характеризуется температурными коэффициентами погрешности полной шкалы и погрешности смещения нуля.
5.2 Динамические параметры
Возникновение динамических погрешностей связано с дискретизацией сигналов, изменяющихся во времени. Можно выделить следующие параметры АЦП, определяющие его динамическую точность.
Максимальная частота дискретизации (преобразования) - это наибольшая частота, с которой происходит образование выборочных значений сигнала, при которой выбранный параметр АЦП не выходит за заданные пределы. Измеряется числом выборок в секунду. Выбранным параметром может быть, например, монотонность характеристики преобразования или погрешность линейности.
Время преобразования (tпр ) - это время, отсчитываемое от начала импульса дискретизации или начала преобразования до появления на выходе устойчивого кода, соответствующего данной выборке. Для одних АЦП, например, последовательного счета или многотактного интегрирования, эта величина является переменной, зависящей от значения входного сигнала, для других, таких как параллельные или последовательно-параллельные АЦП, а также АЦП последовательного приближения, примерно постоянной. При работе АЦП без УВХ время преобразования является апертурным временем.
Время выборки (стробирования) - время, в течение которого происходит образование одного выборочного значения. При работе без УВХ равно времени преобразования АЦП.
5.3 Шумы АЦП
В идеале, повторяющиеся преобразования фиксированного постоянного входного сигнала должны давать один и тот же выходной код. Однако, вследствие неизбежного шума в схемах АЦП, существует некоторый диапазон выходных кодов для заданного входного напряжения. Если подать на вход АЦП постоянный сигнал и записать большое число преобразований, то в результате получится некоторое распределение кодов. Если подогнать Гауссовское распределение к полученной гистограмме, то стандартное отклонение будет примерно эквивалентно среднеквадратическому значению входного шума АЦП. В качестве примера на рис. 26 приведена гистограмма результатов 5000 преобразований постоянного входного сигнала, выполненных 16-разрядным двухтактным последовательно-параллельным АЦП АD7884.
Входное напряжение из диапазона + 5 В было установлено по возможности ближе к центру кода. Как видно из гистограммы, все результаты преобразований распределены на шесть кодов. Среднеквадратическое значение шума, соответствующее этой гистограмме, равно 120 мкВ.
Список используемой литературы
1. Балакай В.Г Интегральные схемы аналого-цифровых преобразователей /Балакай В.Г,Крюк И.П.,Лукьянов Л.М.; Под ред.Лукьянова Л.М. .-М: Энергия, 2008 .-257с.: Ил. .-Библиогрс.251-256.
3. Гельман М.М. Аналого-цифровые преобразователи для информационно-измерительных систем /Гельман М.М. .-М.: Изд-во стандартов, 2009 .-317с.
4. Бирюков С.А. Цифровые устройства на МОП-интегральных микросхемах /Бирюков С.А. .-М.: Радио и связь, 2007 .-129с.: ил. .-(Массовая радиобиблиотека;Вып.1132).
5. Букреев И.Н. Микроэлектронные схемы цифровых устройств /Букреев И.Н. ,Горячев В.И.,Мансуров Б.М. .-3-е изд., перераб. и доп. .-М. : Радио и связь, 2009 .-416с.
6. Гольденберг Л.М. Цифровые устройства на интегральных схемах в технике связи /Гольденберг Л.М.,Бутильский Л.М.,Поляк М.Н. .-М: Связь, 2009 .-232с.
7. Шило В.Л. Популярные цифровые микросхемы: Справочник /Шило В.Л. .-М.: Металлургия, 2008 .-349с. .-(Массовая радиобиблиотека;Вып.1111).
8. Цифровые и аналоговые системы передачи: Учебник для вузов /Иванов В.И., Гордиенко В.Н., Попов Г.Н. и др.; Под ред.Иванова В.И. .-М.: Радио и связь, 2007 .-232с.: ил. .-Библиогр.:с.229-230 .-ISBN 5-256-01226-6.
9. Букреев И.Н. Микроэлектронные схемы цифровых устройств /Букреев И.Н.,Мансуров Б.М.,Горячев В.И. .-2-е изд.,перераб.и доп. .-М.: Сов.радио, 2008 .-368с.: ил. .-Библиогр.:с.364-366.
10. Гольденберг Л.М. Импульсные и цифровые устройства: Учебник для вузов /Гольденберг Л.М. .-М.: Связь, 2009 .-495с.: ил. .-Библиогр.:с.494-495.

