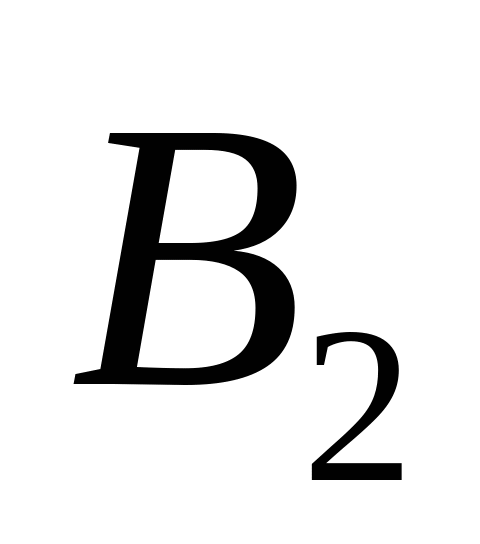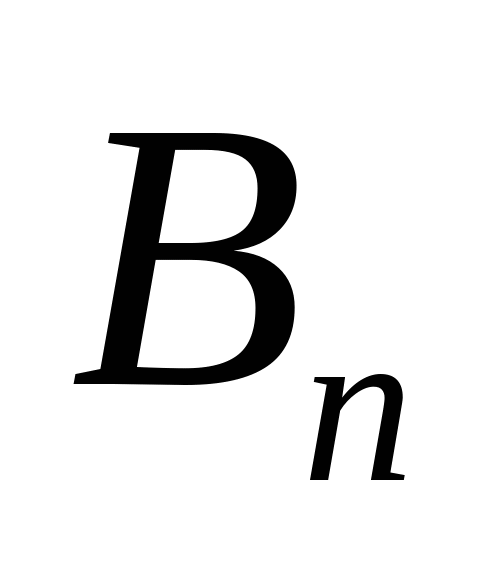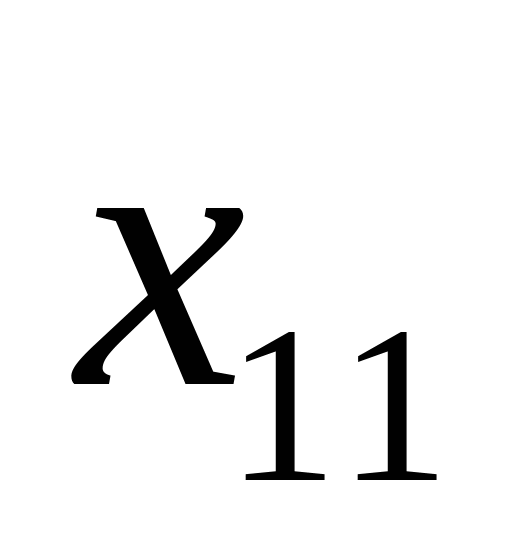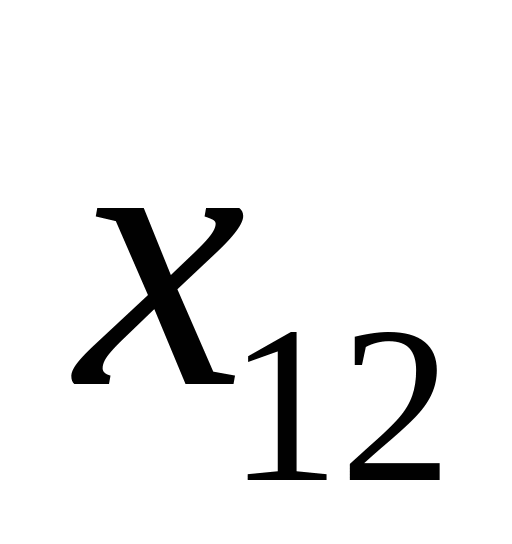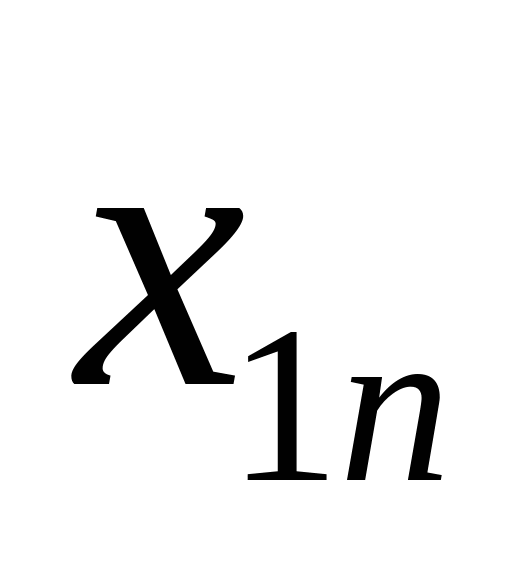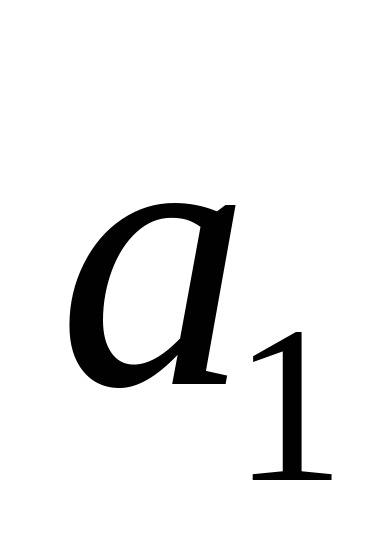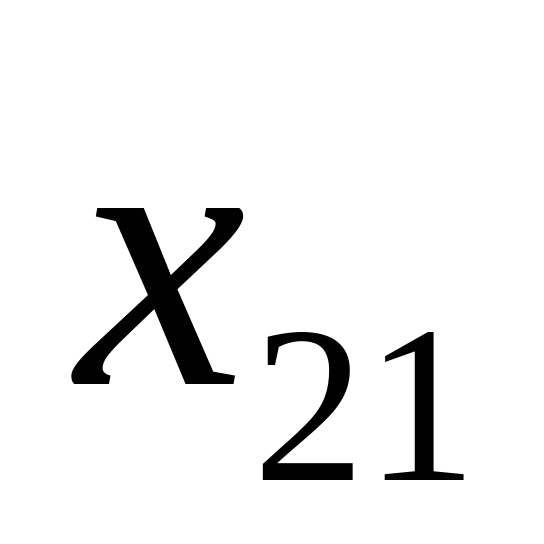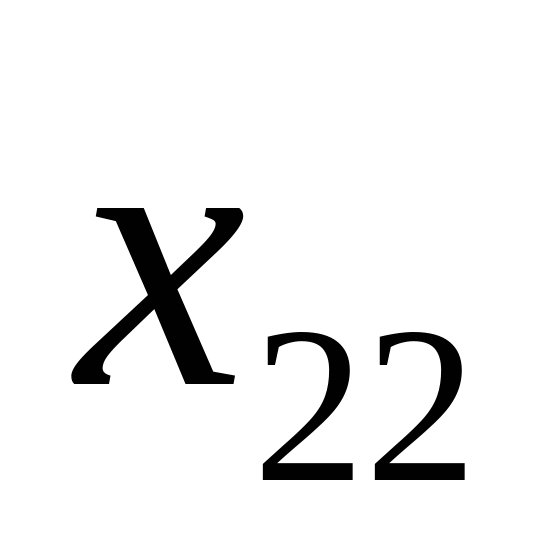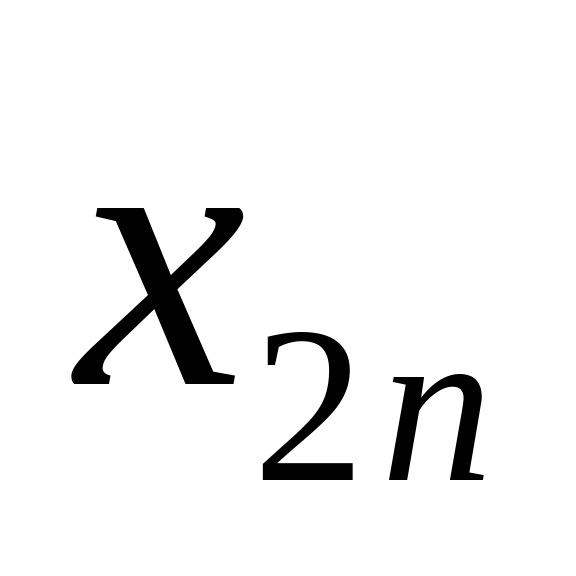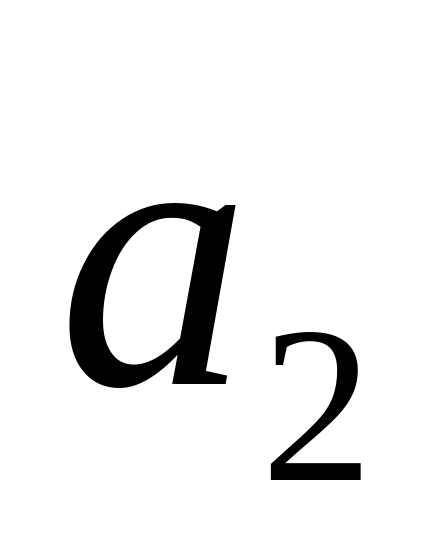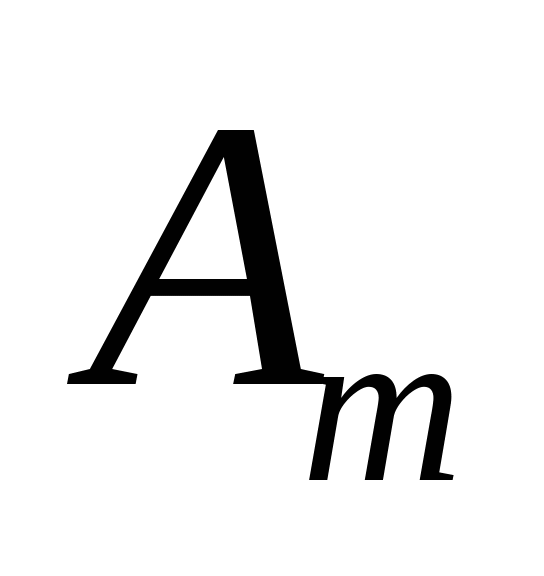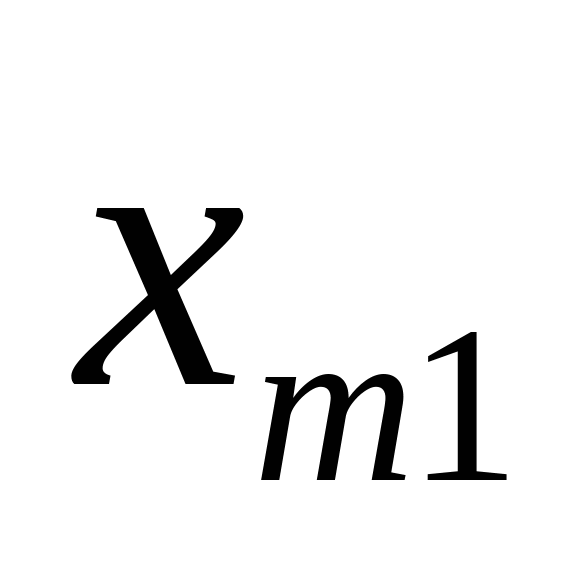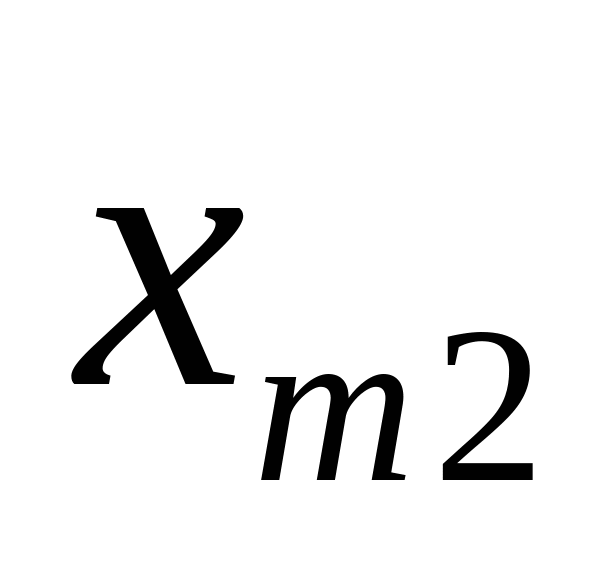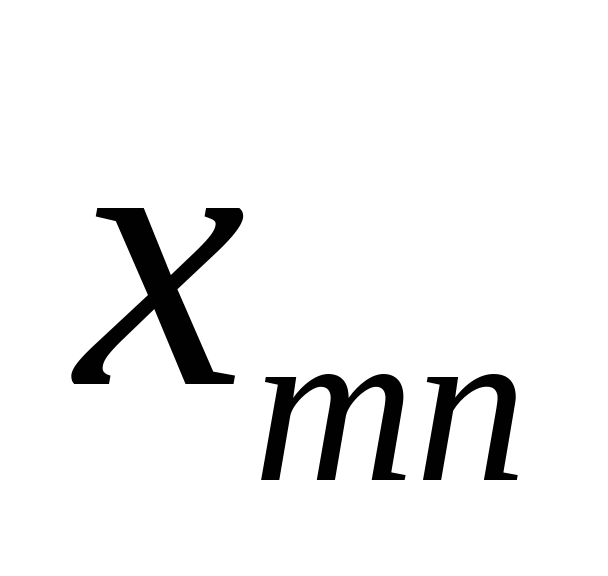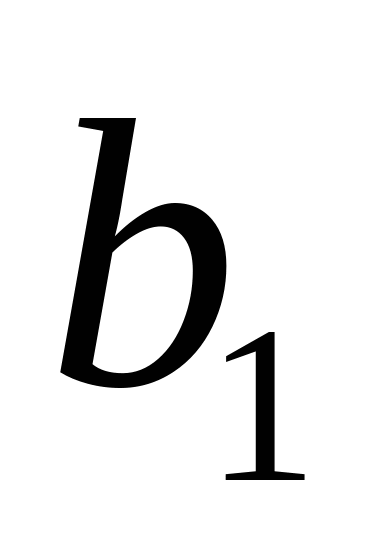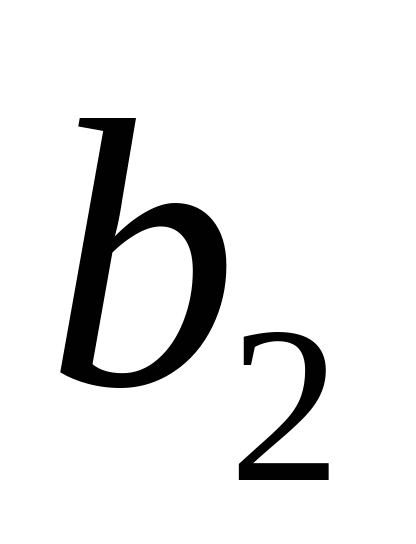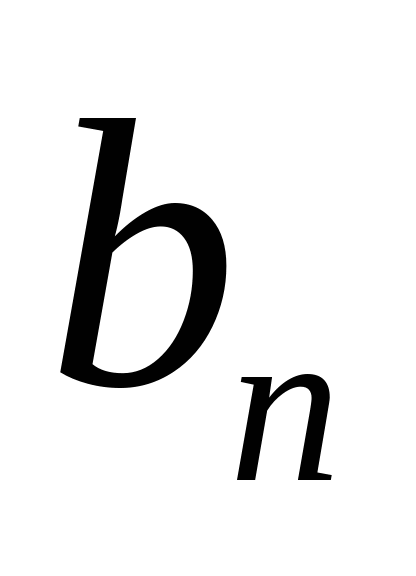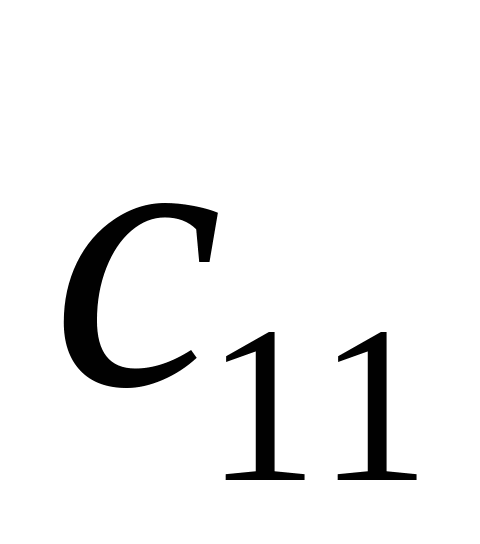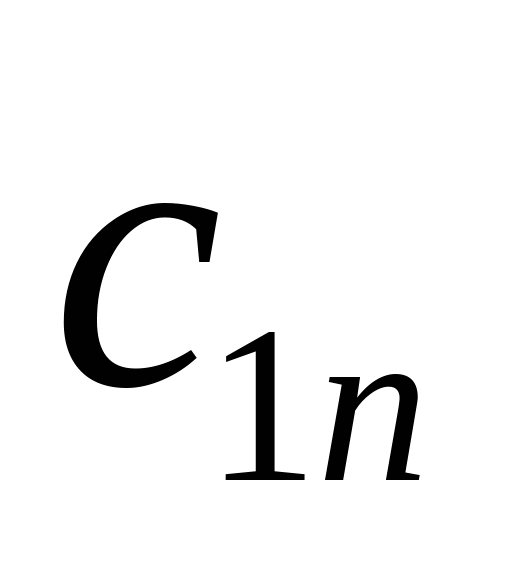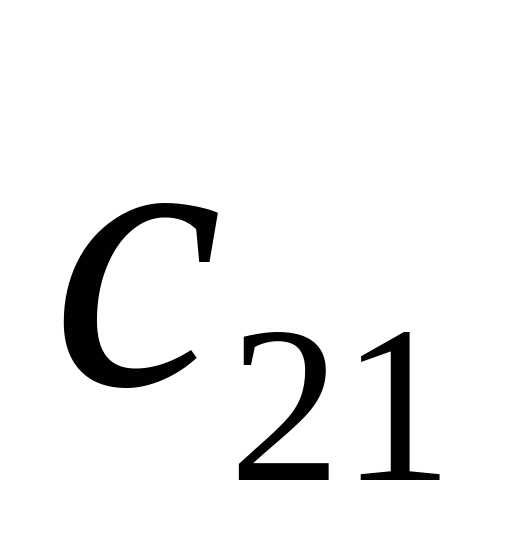Приднестровский государственный университет им. Т. Г. Шевченко
Рыбницкий филиал
Кафедра физики математики и информатики
Курсовая работа
По дисциплине «Исследование операций»
Тема:«Транспортная задача. Венгерский метод»
Выполнил:
Студент IV курса,
специальности «ПОВТиАС»
Козлов Е.В.
Проверила:
преподаватель
Глазова Н.С.
г. Рыбница
2010 г.
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ
Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Классическая транспортная задача – задача о наиболее экономном плане перевозок однородного продукта или взаимозаменяемых продуктов из пунктов производства в пункты потребления, встречается чаще всего в практических приложениях линейного программирования. Линейное программирование является одним из разделов математического программирования – области математики, разрабатывающей теорию и численные методы решения многомерных экстремальных задач с ограничениями.
Огромное количество возможных вариантов перевозок затрудняет получение достаточно экономного плана эмпирическим или экспертным путем. Применение математических методов и вычислительных в планировании перевозок дает большой экономический эффект. Транспортные задачи могут быть решены симплексным методом однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его получить оптимальное решение.
В зависимости от способа представления условий транспортной задачи она может быть представлена в сетевой (схематичной) или матричной (табличной) форме. Транспортная задача может также решаться с ограничениями и без ограничений.
В данной курсовой работе будут рассматриваться математическая постановка транспортной задачи линейного программирования - венгерский метод.
ТРАНСПОРТНАЯ ЗАДАЧА.
ОБЩАЯ ПОСТАНОВКА, ЦЕЛИ, ЗАДАЧИ. ОСНОВНЫЕ ТИПЫ, ВИДЫ МОДЕЛЕЙ.
Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.
В общей постановке транспортная задача состоит в отыскании оптимального плана перевозок некоторого однородного груза с 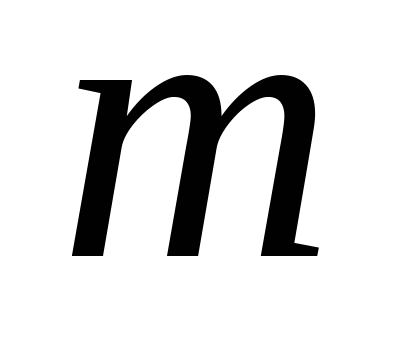 баз
баз 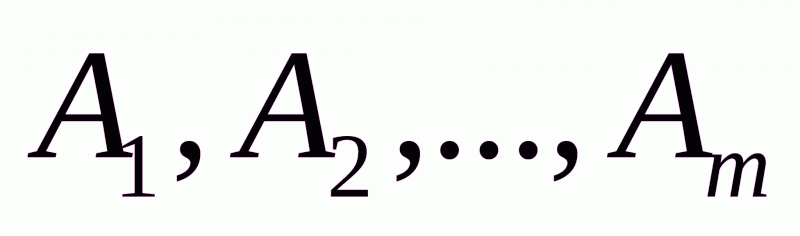
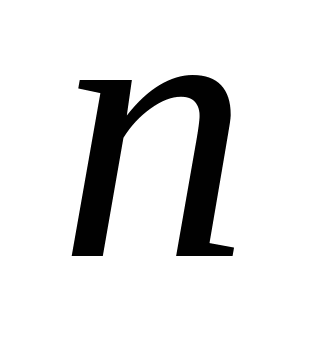 потребителям
потребителям 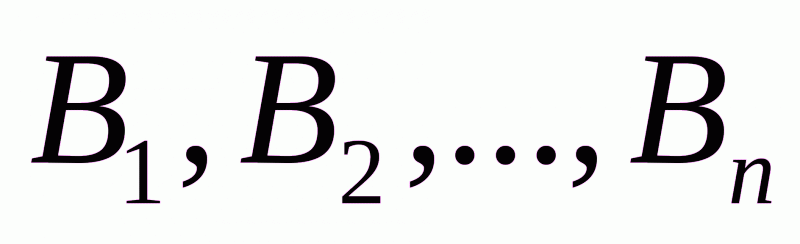 .
.
Различают два типа транспортных задач: но критерию стоимости (план перевозок оптимален, если достигнут минимум затрат на его реализацию) и по критерию времени (план оптимален, если на его реализацию затрачивается минимум времени).
Обозначим количество груза, имеющегося на каждой из 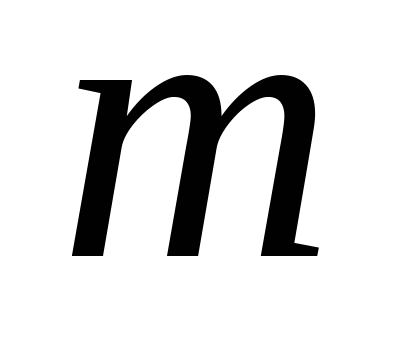 баз(запасы), соответственно
баз(запасы), соответственно 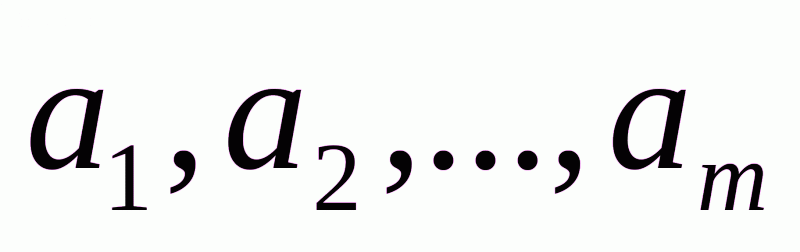 ,а общее количество имеющегося в наличии груза–
,а общее количество имеющегося в наличии груза– :
:
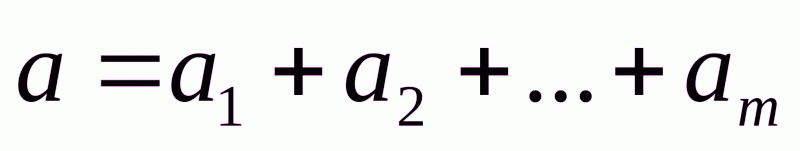
(1.1)
;з
(1.2)
аказы каждого из потребителей (потребности) обозначим соответственно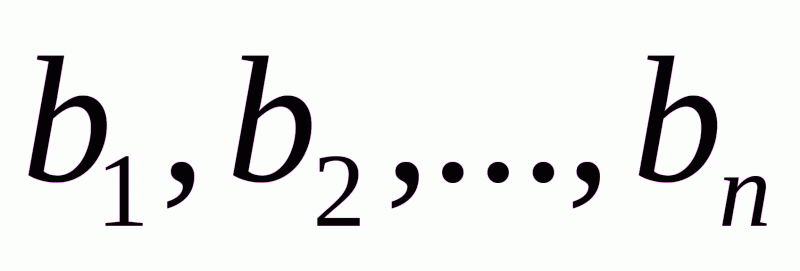 , а общее количество потребностей –
, а общее количество потребностей –  :
: 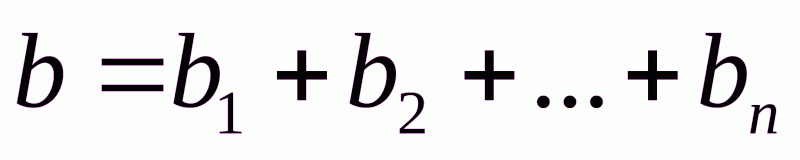 ,
,
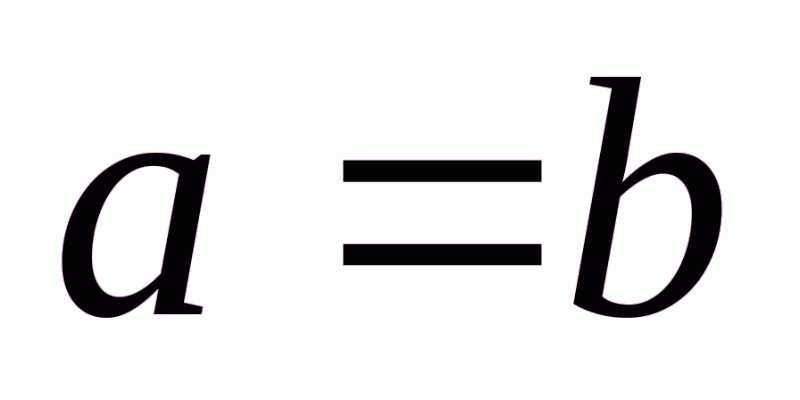
(1.3)
мы имеем закрытую модель, а при условии

(1.4)
– открытую модель транспортной задачи.
Очевидно, в случае закрытой модели весь имеющийся в наличии груз развозится полностью, и все потребности заказчиков полностью удовлетворены; в случае же открытой модели либо все заказчики удовлетворены и при этом на некоторых базах остаются излишки груза 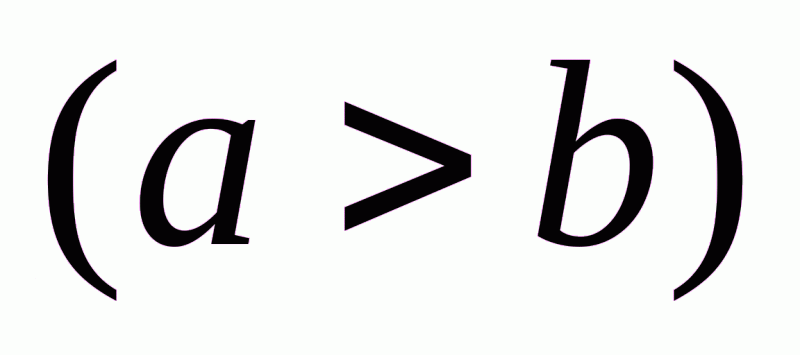 , либо весь груз оказывается израсходованным, хотя потребности полностью не удовлетворены
, либо весь груз оказывается израсходованным, хотя потребности полностью не удовлетворены 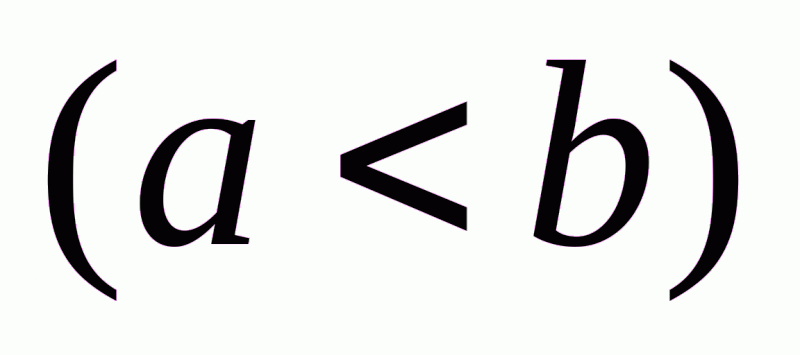 .
.
Так же существуют одноэтапные модели задач, где перевозка осуществляется напрямую от, например, базы или завода изготовителя к потребителю, и двухэтапные, где между ними имеется “перевалочный пункт”, например – склад.
План перевозок с указанием запасов и потребностей удобно записывать в виде следующей таблицы, называемой таблицей перевозок:
| Пункты Отправления | Пункты назначения | Запасы | |||
|
|
| … |
| ||
|
|
|
| … |
|
|
|
|
|
| … |
|
|
| … | … | … | … | … | … |
|
|
|
| … |
|
|
| Потребности |
|
| … |
|
или
|
Условие 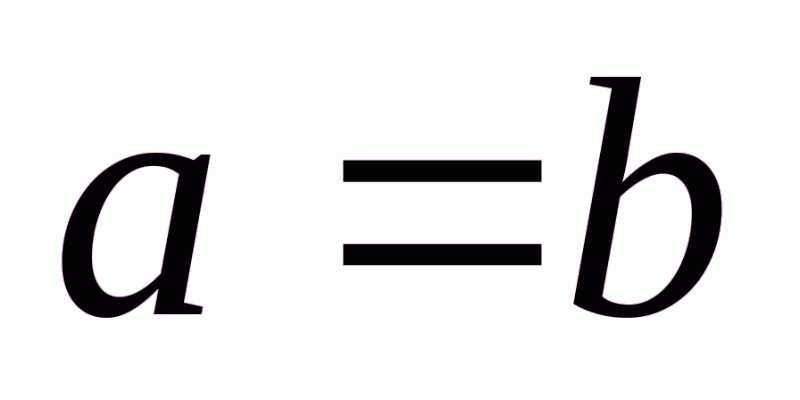 или
или  означает, с какой задачей мы имеем дело, с закрытой моделью или открытой моделью транспортной задачи. Переменное
означает, с какой задачей мы имеем дело, с закрытой моделью или открытой моделью транспортной задачи. Переменное 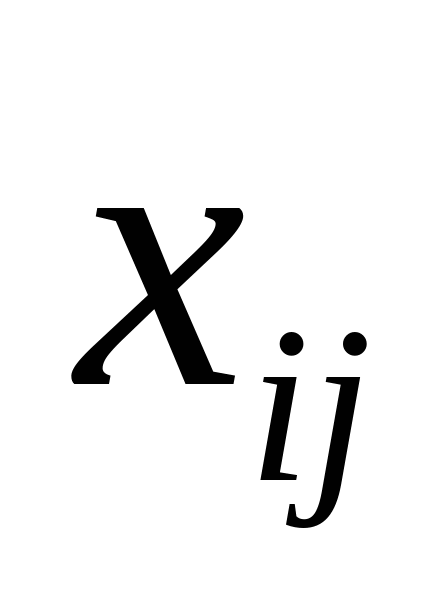 означает количество груза, перевозимого с базы
означает количество груза, перевозимого с базы  потребителю
потребителю 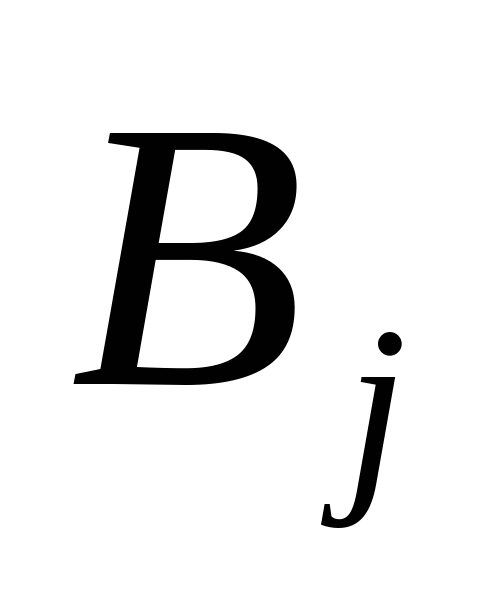 : совокупность этих величин образует матрицу (матрицу перевозок).
: совокупность этих величин образует матрицу (матрицу перевозок).
Очевидно, переменные 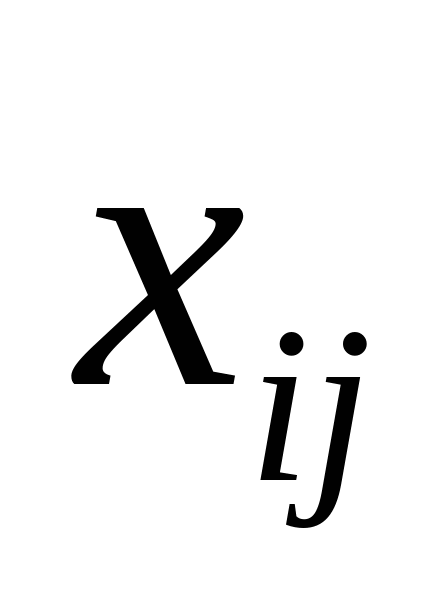 должны удовлетворять условиям:
должны удовлетворять условиям:

![]()
(2.1)
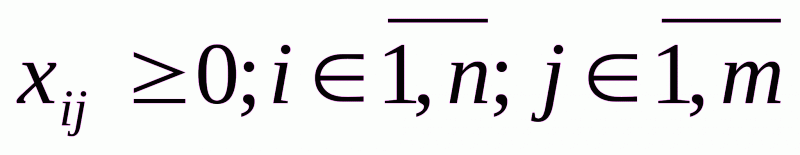
(2.1.1)
Система (2.1) содержит 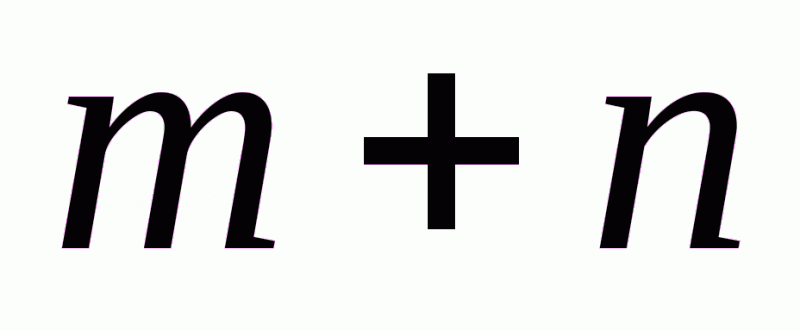 уравнений с
уравнений с 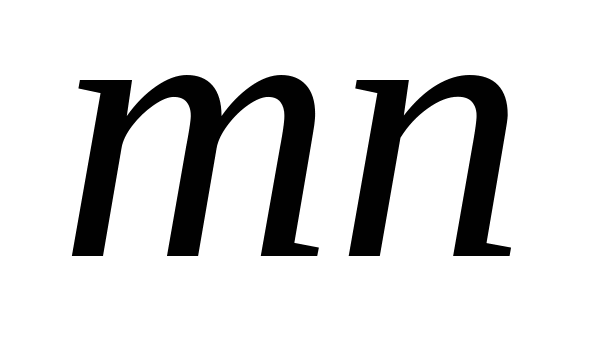 неизвестными. Её особенность состоит в том, что коэффициенты при неизвестных всюду равны единице. Кроме того, все уравнения системы (2.1) могут быть разделены на две группы: первая группа из т первых уравнений (“горизонтальные” уравнения) и вторая группа из п остальных уравнений (“вертикальные” уравнения). В каждом из горизонтальных уравнений содержатся неизвестные с одним и тем же первым индексом (они образуют одну строку матрицы перевозок), в каждом из вертикальных уравнений содержатся неизвестные с одним и тем же вторым индексом (они образуют один столбец матрицы перевозок). Таким образом, каждая неизвестная встречается в системе (2.1) дважды: в одном и только одном горизонтальном и в одном и только одном вертикальном уравнениях.
неизвестными. Её особенность состоит в том, что коэффициенты при неизвестных всюду равны единице. Кроме того, все уравнения системы (2.1) могут быть разделены на две группы: первая группа из т первых уравнений (“горизонтальные” уравнения) и вторая группа из п остальных уравнений (“вертикальные” уравнения). В каждом из горизонтальных уравнений содержатся неизвестные с одним и тем же первым индексом (они образуют одну строку матрицы перевозок), в каждом из вертикальных уравнений содержатся неизвестные с одним и тем же вторым индексом (они образуют один столбец матрицы перевозок). Таким образом, каждая неизвестная встречается в системе (2.1) дважды: в одном и только одном горизонтальном и в одном и только одном вертикальном уравнениях.
Такая структура системы (2.1) позволяет легко установить ее ранг. Действительно, покажем, что совокупность неизвестных, образующих первую строку и первый столбец матрицы перевозок, можно принять в качестве базиса. При таком выборе базиса, по крайней мере, один из двух их индексов равен единице, а, следовательно, свободные неизвестные определяются условием 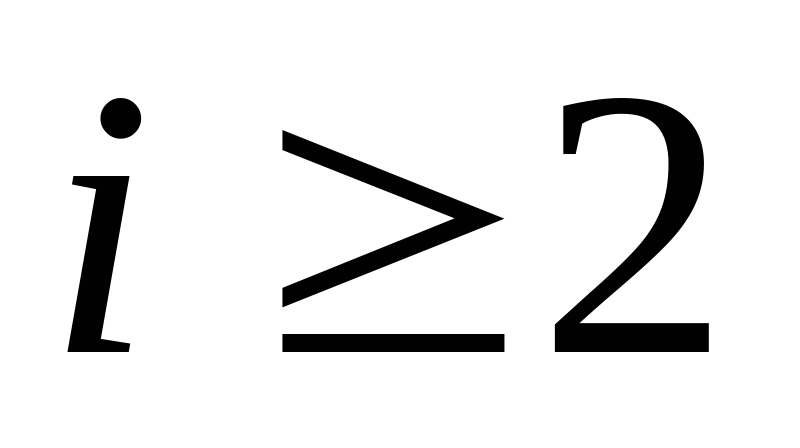 ,
,  .Перепишем систему (2.1) в виде
.Перепишем систему (2.1) в виде
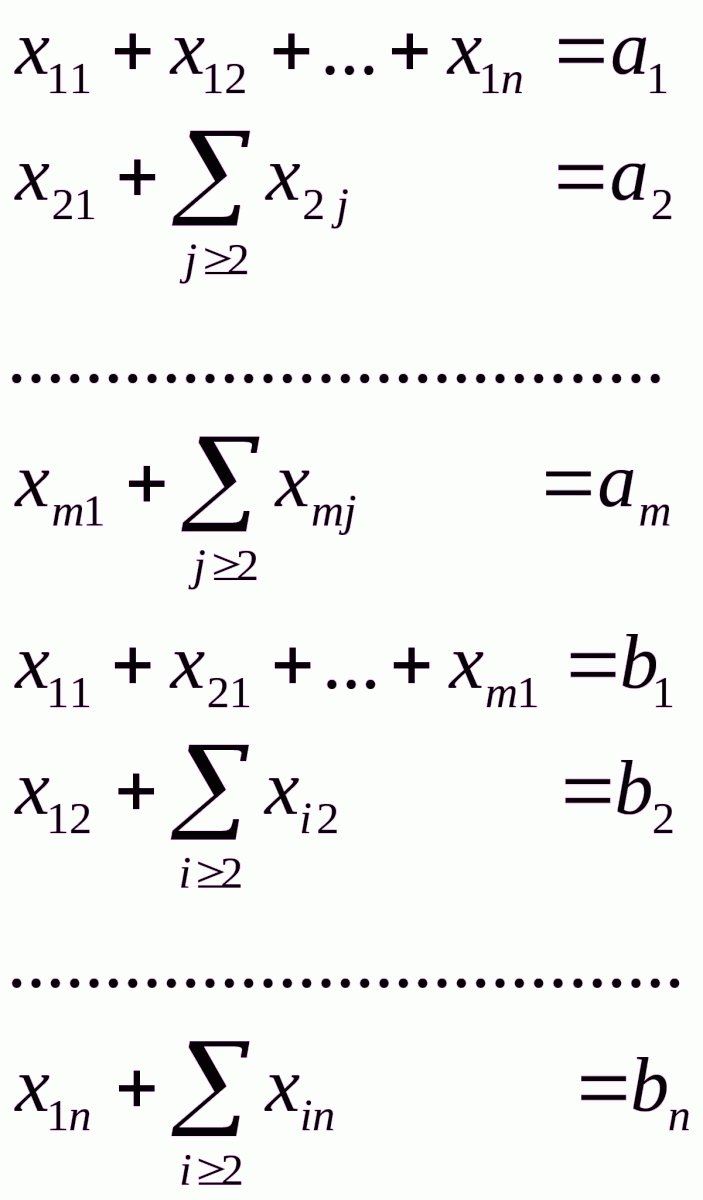
(2.1’)
где символы 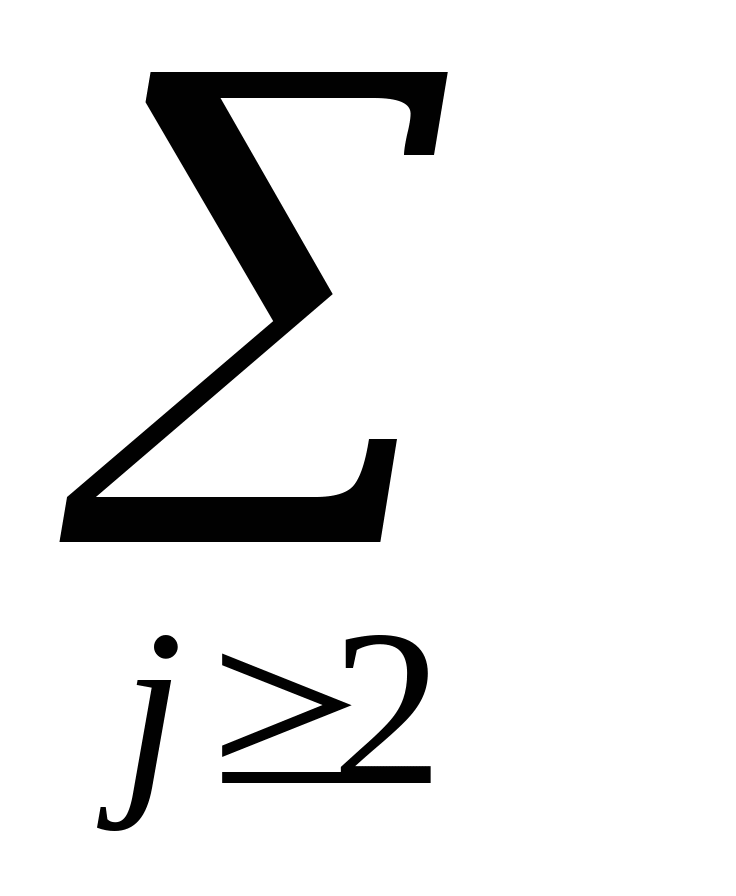 и
и 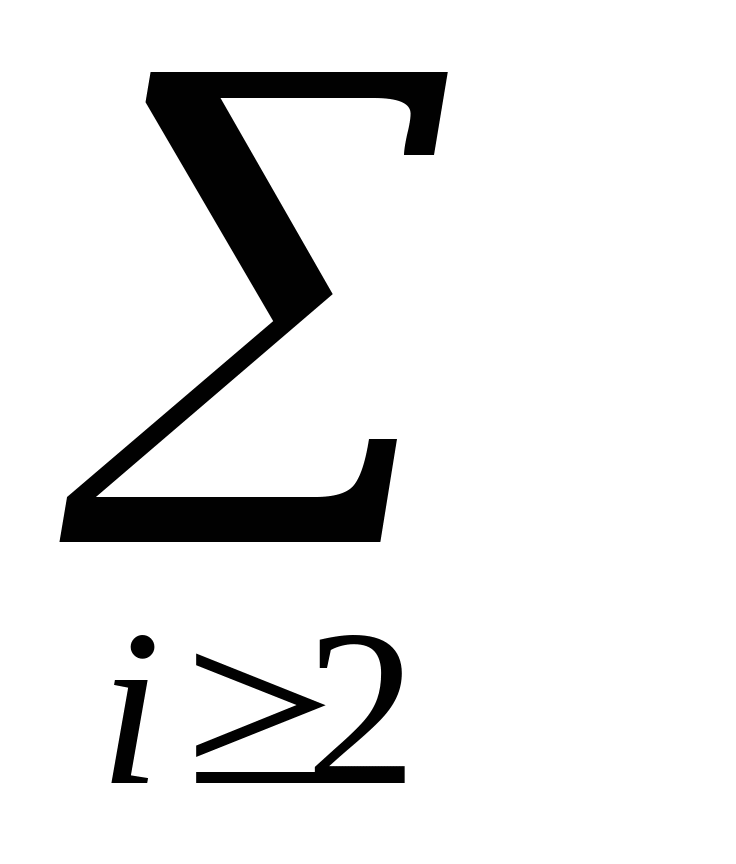 означают суммирование по соответствующему индексу. Так, например,
означают суммирование по соответствующему индексу. Так, например,
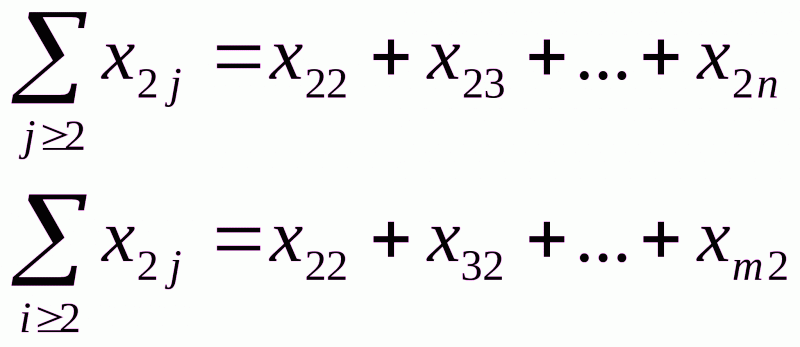
При этом легко заметить, что под символами такого суммирования объединяются только свободные неизвестные (здесь 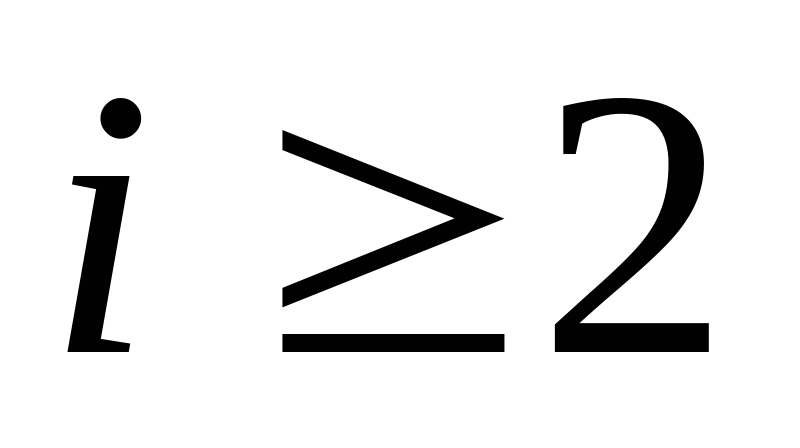 ,
,  ).
).
В рассматриваемой нами системе только два уравнения, а именно первое горизонтальное и первое вертикальное, содержат более одного неизвестного из числа выбранных нами для построения базиса. Исключив из первого горизонтального уравнения базисные неизвестные 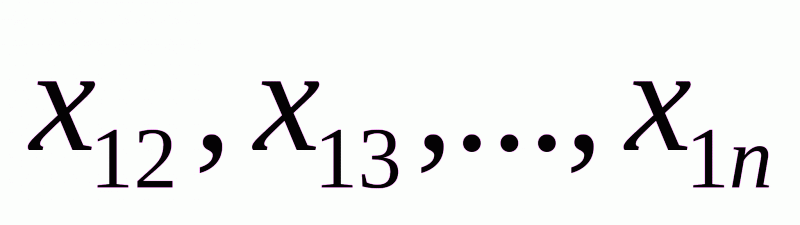 с помощью вертикальных уравнений, мы получаем уравнение
с помощью вертикальных уравнений, мы получаем уравнение
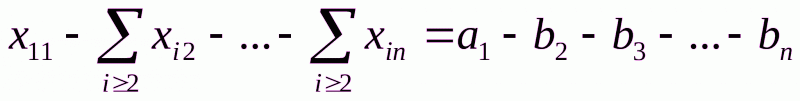
и
(2.2)
ли короче 
где символ 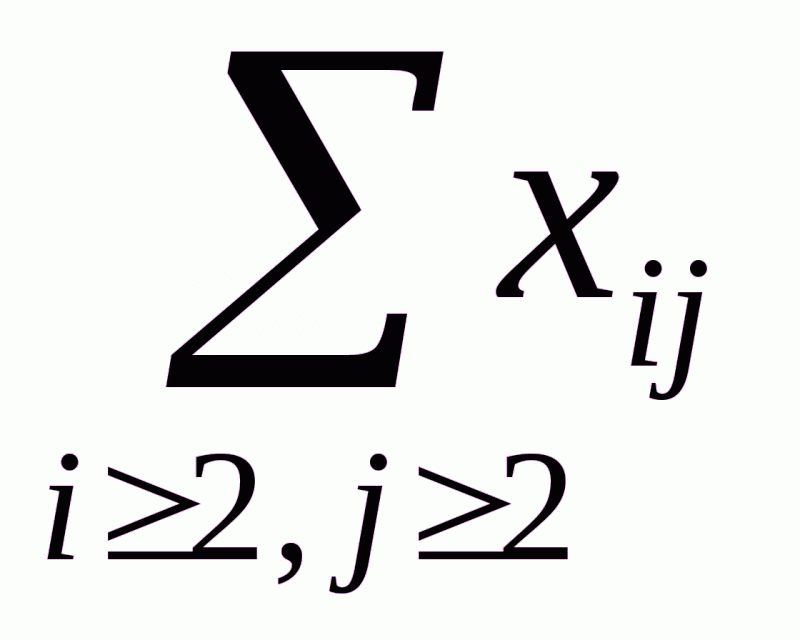 означает сумму всех свободных неизвестных. Аналогично, исключив из первого вертикального уравнения базисные неизвестные
означает сумму всех свободных неизвестных. Аналогично, исключив из первого вертикального уравнения базисные неизвестные 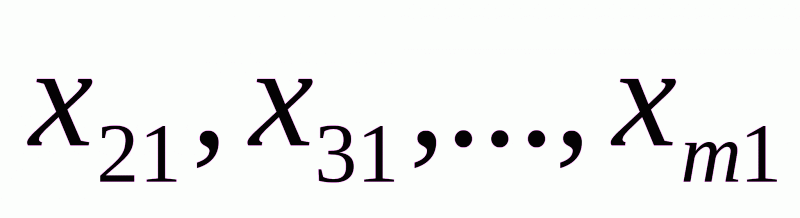 с помощью горизонтальных уравнений, мы получаем уравнение
с помощью горизонтальных уравнений, мы получаем уравнение

(2.2’)
Так как для закрытой модели транспортной задачи 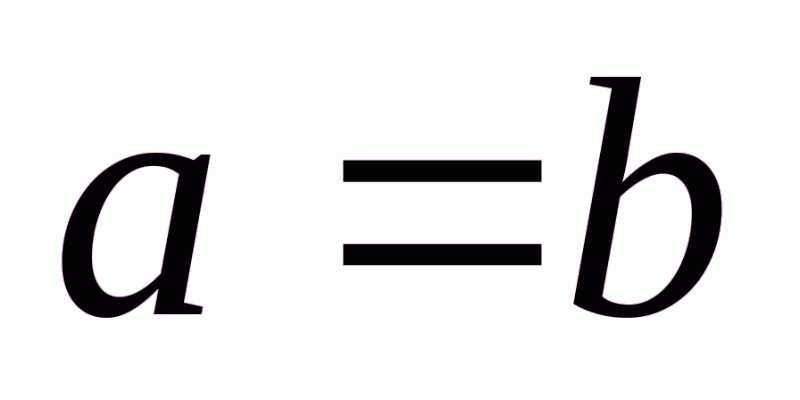 , то полученные нами уравнения (2.2) и (2.2’) одинаковы и, исключив из одного из них неизвестное
, то полученные нами уравнения (2.2) и (2.2’) одинаковы и, исключив из одного из них неизвестное  , мы получим уравнение-тождество 0=0, которое из системы вычеркивается.
, мы получим уравнение-тождество 0=0, которое из системы вычеркивается.
И![]() так, преобразование системы (2.1) свелось к замене двух уравнений (первого горизонтального и первого вертикального) уравнением (2.2). Остальные уравнения остаются неизменными. Система приняла вид
так, преобразование системы (2.1) свелось к замене двух уравнений (первого горизонтального и первого вертикального) уравнением (2.2). Остальные уравнения остаются неизменными. Система приняла вид
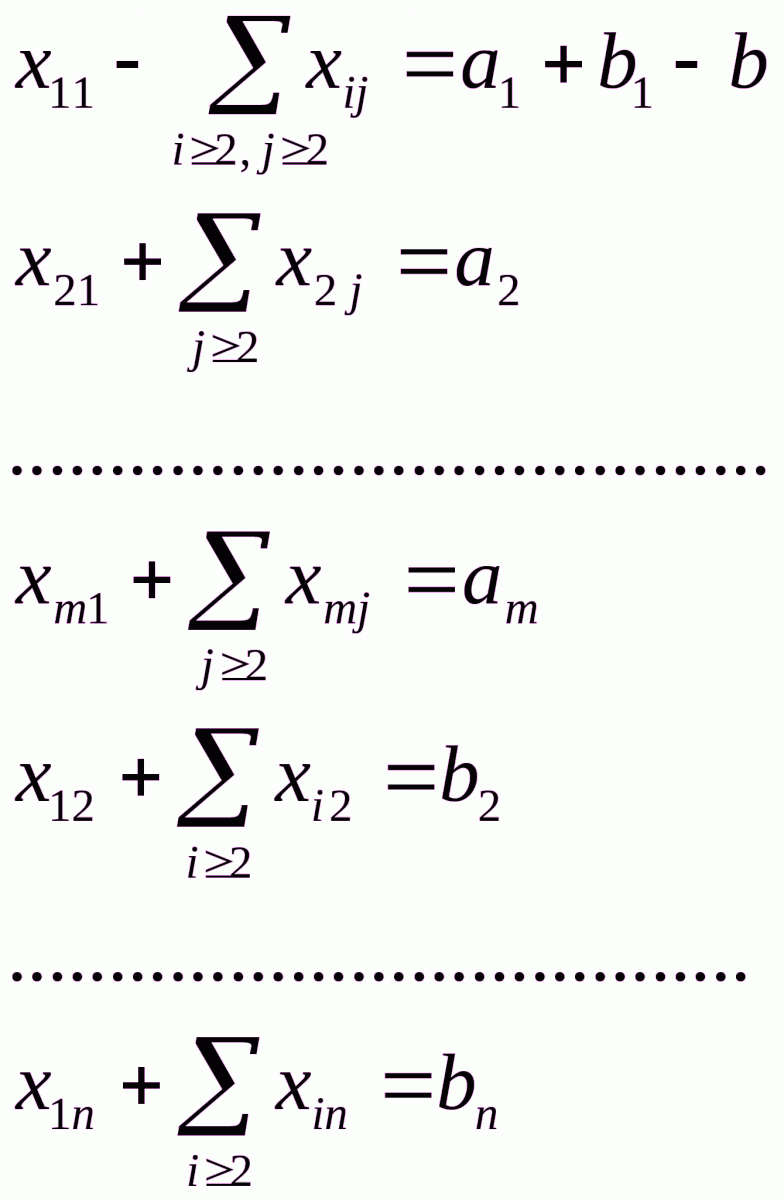
(2.3)
В системе (2.3) выделен указанный выше базис: базисные неизвестные из первых т уравнений образуют первый столбец матрицы перевозок, а базисные неизвестные остальных уравнений образуют первую строку матрицы перевозок без первого неизвестного  [она входит в первое уравнение системы (2.3)]. В системе (2.3) имеется
[она входит в первое уравнение системы (2.3)]. В системе (2.3) имеется 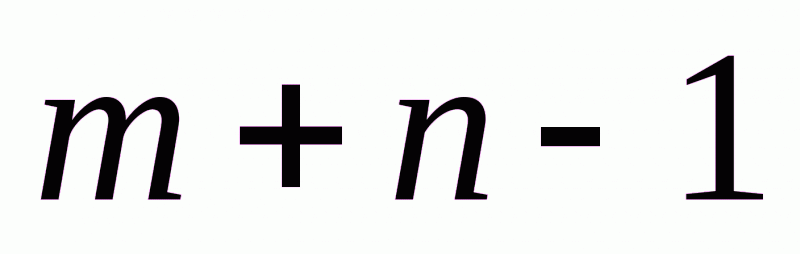 уравнений, выделенный базис содержит
уравнений, выделенный базис содержит 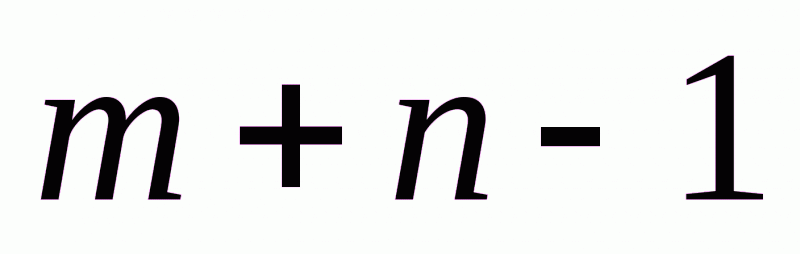 неизвестных, а, следовательно, и ранг системы (2.1)
неизвестных, а, следовательно, и ранг системы (2.1) 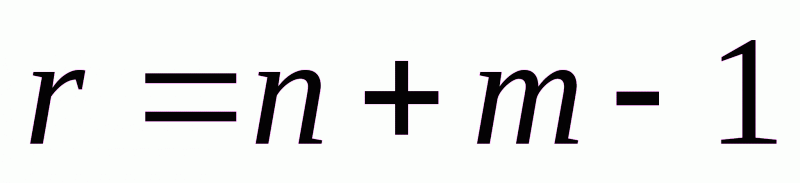 .
.
Для решения транспортной задачи необходимо кроме запасов и потребностей знать также и тарифы  , т. е. стоимость перевозки единицы груза с базы
, т. е. стоимость перевозки единицы груза с базы  потребителю
потребителю 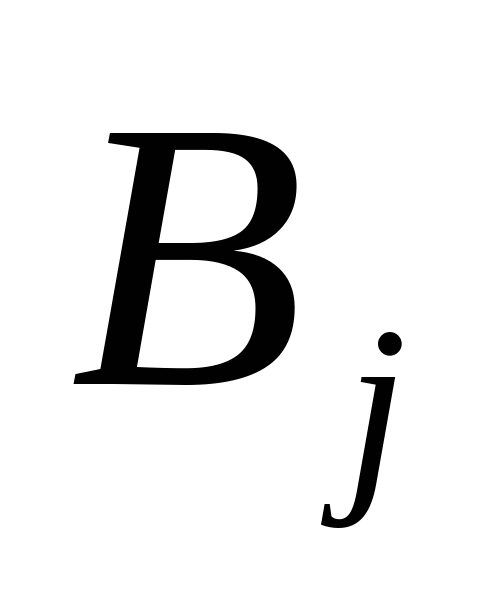 .
.
Совокупность тарифов  также образует матрицу, которую можно объединить с матрицей перевозок и данными о запасах и потребностях в одну таблицу:
также образует матрицу, которую можно объединить с матрицей перевозок и данными о запасах и потребностях в одну таблицу:
| Пункты Отправления | Пункты назначения | Запасы | ||||||||
|
|
| … |
| |||||||
|
|
|
| … |
|
| |||||
|
|
|
| ||||||||
|
|
|
| … |
|
| |||||
|
|
|
| ||||||||
| … | … | … | … | … | … | |||||
|
|
|
| … |
|
| |||||
|
|
|
| ||||||||
| Потребности |
|
| … |
|
или
| |||||
Сумма всех затрат, т. е. стоимость реализации данного плана перевозок, является линейной функцией переменных 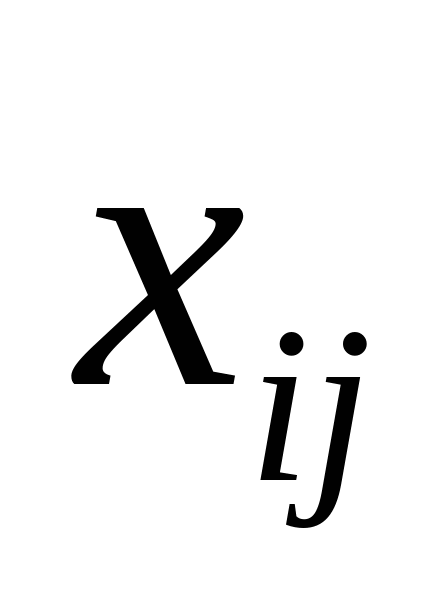 :
:
(2.4)
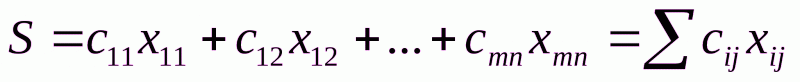
Требуется в области допустимых решений системы уравнений (2.1) и (2.1.1) найти решение, минимизирующее линейную функцию (2.4).
Таким образом, мы видим, что транспортная задача является задачей линейного программирования. Для ее решения применяют также симплекс-метод, но в силу специфики задачи здесь можно обойтись без симплекс-таблиц. Решение можно получить путем некоторых преобразований таблицы перевозок. Эти преобразования соответствуют переходу от одного плана перевозок к другому. Но, как и в общем случае, оптимальное решение ищется среди базисных решений. Следовательно, мы будем иметь дело только с базисными (или опорными) планами. Так как в данном случае ранг системы ограничений-уравнений равен 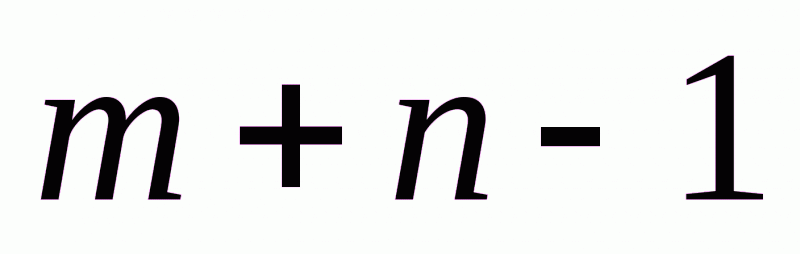 то среди всех
то среди всех 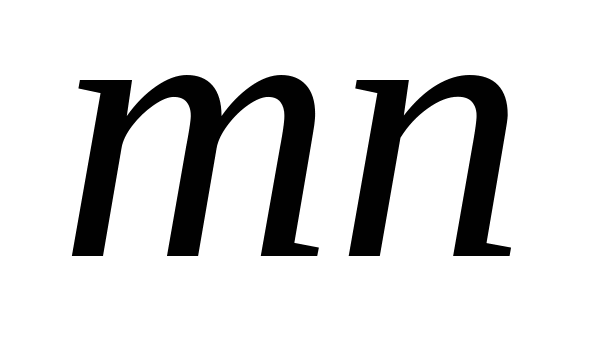 неизвестных
неизвестных 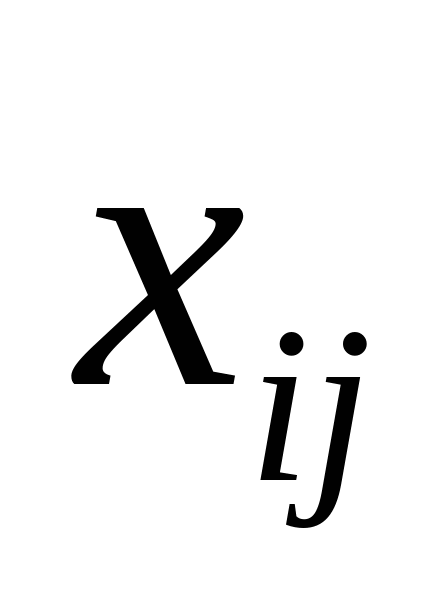 выделяется
выделяется 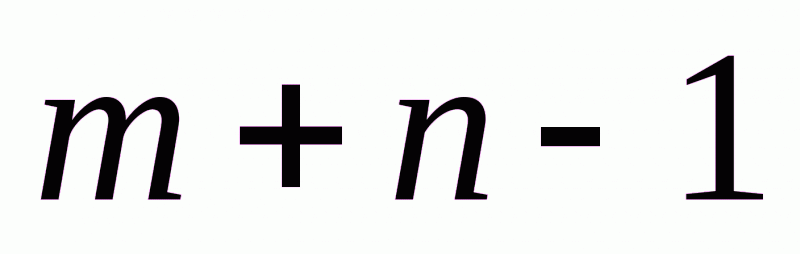 базисных неизвестных, а остальные
базисных неизвестных, а остальные 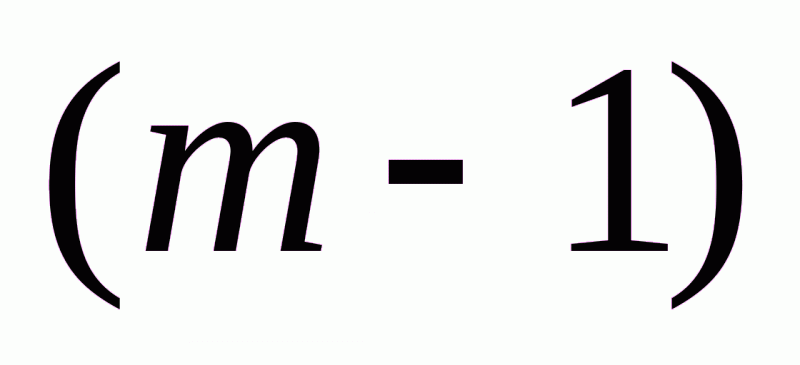 ·
·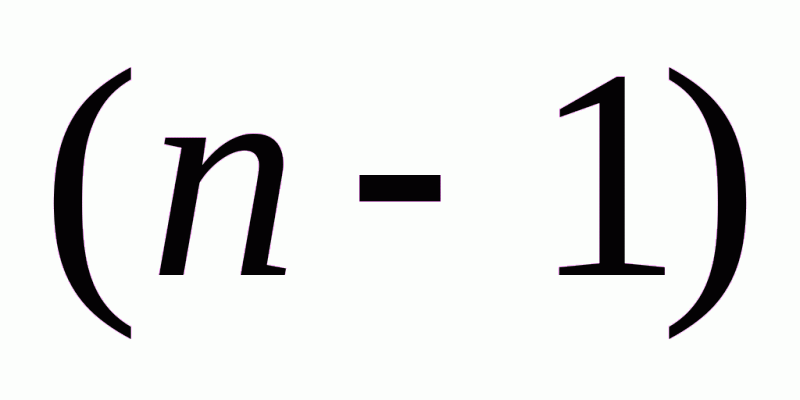
неизвестных являются свободными. В базисном решении свободные неизвестные равны нулю. Обычно эти нули в таблицу не вписывают, оставляя соответствующие клетки пустыми. Таким образом, в таблице перевозок, представляющей опорный план, мы имеем 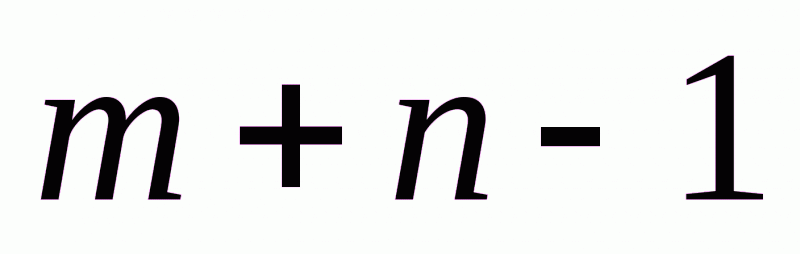 заполненных и
заполненных и 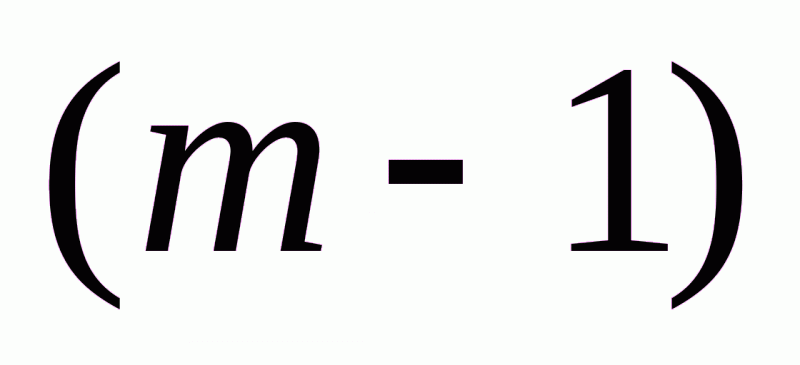 ·
·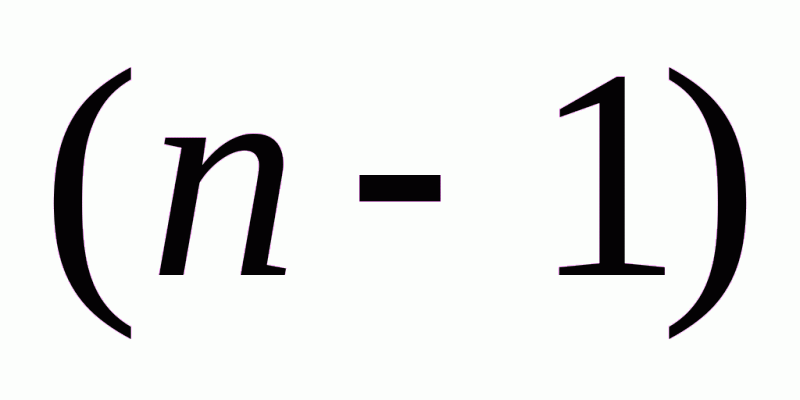 пустых клеток.
пустых клеток.
Для контроля надо проверять, равна ли сумма чисел в заполненных клетках каждой строки таблицы перевозок запасу груза на соответствующей базе, а в каждом столбце — потребности заказчика [этим подтверждается, что данный план является решением системы (2.1)].
Замечание 1. Не исключаются здесь и вырожденные случаи, т. е. возможность обращения в нуль одной или нескольких базисных неизвестных. Но эти нули в отличие от нулей свободных неизвестных вписываются в соответствующую клетку, и эта клетка считается заполненной.
Замечание 2. Под величинами  , очевидно, не обязательно подразумевать только тарифы. Можно также считать их величинами, пропорциональными тарифам, например, расстояниями от баз до потребителей. Если, например,
, очевидно, не обязательно подразумевать только тарифы. Можно также считать их величинами, пропорциональными тарифам, например, расстояниями от баз до потребителей. Если, например, 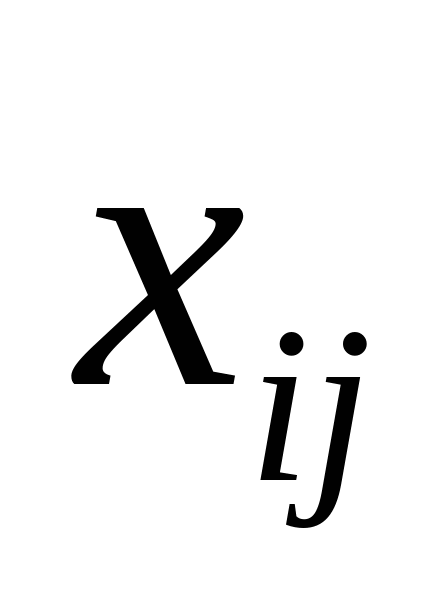 выражены в тоннах, а
выражены в тоннах, а  в километрах, то величина
в километрах, то величина 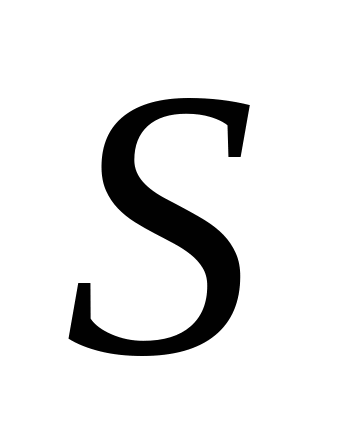 , определяемая формулой (2.4), является количеством тонно-километров, составляющих объем данного плана перевозок. Очевидно, что затраты на перевозки пропорциональны количеству тонно-километров и, следовательно, будут минимальными при минимуме S. В этом случае вместо матрицы тарифов мы имеем матрицу расстояний.
, определяемая формулой (2.4), является количеством тонно-километров, составляющих объем данного плана перевозок. Очевидно, что затраты на перевозки пропорциональны количеству тонно-километров и, следовательно, будут минимальными при минимуме S. В этом случае вместо матрицы тарифов мы имеем матрицу расстояний.