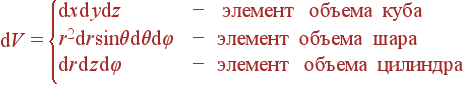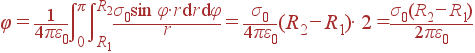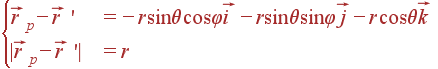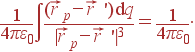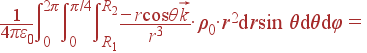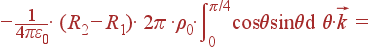М.И. Векслер, Г.Г. Зегря
Пусть
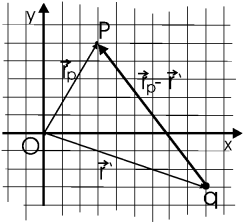
O - начало координат, P - точка, в которой ищется поле, A - точка, в которой
расположен заряд q. Вектор  обычно обозначают
обычно обозначают 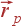 ,
вектор
,
вектор  обозначают
обозначают 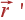 . Тогда
напряженность электрического поля и потенциал, создаваемые зарядом, записываются
как:
. Тогда
напряженность электрического поля и потенциал, создаваемые зарядом, записываются
как:
|

|
(1) |
Задача.
Найти поле, которое в точке  создает
заряд q, находящийся в точке
создает
заряд q, находящийся в точке  .
.
Ответ:
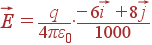
При
наличии распределенного заряда, создающего поле, необходимо провести
интегрирование:
|

|
(2) |
При
этом 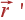 пробегает всевозможные положения из начала координат в точки, где
есть заряд dq. Последний записывается как
пробегает всевозможные положения из начала координат в точки, где
есть заряд dq. Последний записывается как
Если
рассматривается равномерно заряженная зарядом Q объемная (объема V), поверхностная
(площади S) или линейная (длины L) область, то, соответственно,
|
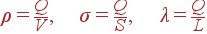
|
(3) |
Как
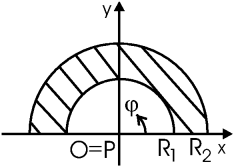
записать dV, dS и dl? Это зависит исключительно от геометрии:
Задача.
Нить, равномерно заряженная с плотностью λ0, имеет длину 2a и расположена
в плоскости xy вдоль оси x симметрично относительно оси y. Найти поле на оси y
как функцию y.
Ответ:
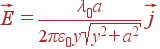
Задача.
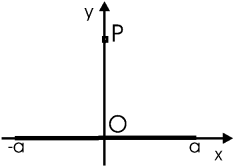
Найти потенциал в центре пластины в форме полудиска. Внутренний и внешний
радиусы R1 и R2, заряд σ = σ0sinφ, где φ- угол в плоскости
xy.
Решение:
Потенциал рассчитываем по стандартной формуле (2):
При
этом
Соответственно,
С
учетом формы тела, создающего поле,
| dq = σ(r, φ)· dS = σ0sinφ· rdr dφ |
|
|
|
причем
φ изменяется в пределах от 0 до π, а r - от R1 до R2. Теперь можно
продолжить интегрирование формулы для φ:
Задача.
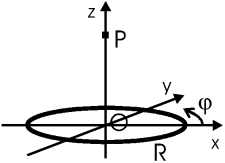
Найти поле на оси кольца радиуса R, заряженного как λ = λ0cosφ.
Кольцо расположено в плоскости xy.
Ответ:
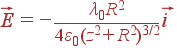
Задача.
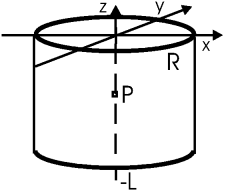
Найти потенциал на оси z цилиндрической поверхности радиуса R. Цилиндр заряжен
как σ = σ0cosφ и расположен соосно с z, занимая область –L... 0.
Ответ:
φ(z) = 0
Задача.
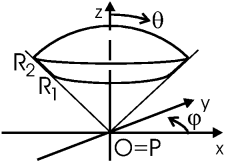
Найти поле в центре шарового сектора с внутренним и внешним радиусами R1, R2, занимающего
область φ = 0... 2π, θ = 0... π/4, равномерно заряженного
зарядом ρ0.
Решение:
Заряженный объект (шаровой сектор) является объемным, так что
| dq = ρ dV = ρ0· r2drsinθdθdφ |
|
|
|
где
использовано выражение для элемента объема шара. У нас начало координат совпадает
с точкой, где ищется поле, так что
Вектор
 запишется:
запишется:
При
этом
Теперь
у нас уже есть все составные компоненты для проведения интегрирования. Пределы
интегрирования вытекают из условия задачи:
Совершенно
очевидно, что члены, содержащие cosφ или sin φ, при интегрировании по
φ от 0 до 2π дадут ноль (это интегрирование по периоду), поэтому их
можно дальше не выписывать.
Направление
вектора 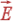 против оси z естественно из симметрии задачи. Если заряд
положителен, то поле должно быть ориентировано от заряженного сектора, что и
имеет место.
против оси z естественно из симметрии задачи. Если заряд
положителен, то поле должно быть ориентировано от заряженного сектора, что и
имеет место.
Список литературы
1.
И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448
с.; или 2-е изд., М.: Наука, 1988. - 416 с.
2.
В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М.
Бредова), 2-е изд., М.: Наука, 1970. - 503 с.
3. Л.Д. Ландау, Е.М. Лифшиц, Теоретическая физика. т.8 Электродинамика сплошных сред, 2-е изд., М.:
Наука, 1992. - 661 с.
Для
подготовки данной работы были использованы материалы с сайта edu.ioffe/r
Другие работы по теме:
Владельцы леса и экология
Считается, что Россия - самая богатая лесами страна в мире: доля наших лесов по запасам составляет около 22%. Но почему-то все чаще приходится слышать об истощенности российских лесов.Проблема экологии в России.
Электрический заряд. Закон Кулона
Подобно понятию гравитационной массы тела в механике Ньютона, понятие заряда в электродинамике является первичным, основным понятием. Электрический заряд
Электрический заряд 2
Реферат по физике по §1-6 Витенбек Марии Электрический заряд Электрический заряд — это связанное с телом свойство, позволяющее ему быть источником электрического поля и участвовать в электромагнитных взаимодействиях. Заряд является количественной характеристикой. Единица измерения заряда в СИ — кулон — электрический заряд, проходящий через поперечное сечение проводника при силе тока 1А за время 1с.
Электростатическая защита
ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ Электростатическое поле - эл.поле, образованное неподвижными электрическими зарядами. Свободные электроны - электроны, способные свободно перемещаться внутри проводника ( в основном в металлах) под действием эл. поля;
Основные законы и формулы физики
1АнтиМВХиР v. 950419 2О С Н О В Н Ы Е Ф О Р М У Л Ы И З А К О Н Ы 0 2Ф И З И К И 3МЕХАНИКА 2Упругие деформации. 1Закон Гука 0: 21 0) при малых деформациях сила упругости пропорциональна абсолютной деформации и направлена противоположно смещению.
Основные вопросы теории электрических цепей
Какое устройство используют для накопления заряда. Понятие электрического тока. Условия возникновения электродвижущей силы. Сила тока и его мощность. Закон Ома для участка сети. Электронапряженность и электропроницаемость. Проводники и диэлектрики.
Электродинамика
Електродинаміка – розділ фізики в якому вивчаються електричні й магнітні явища. Основу цих явищ становить електромагнітна взаємодія основними положеннями термодинаміки є заряд і електромагнітне поле.
Электрическое поле
Работа по физике Ученика 10 класса А Школы №1202 Круглова Егора Электрическое поле По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве
Примерные экзаменационные билеты по физике (11 класс)
Примерные экзаменационные билеты по физике Билет №1 Механическое движение. Относительность движения. Система отсчета. Материальная точка. Траектория. Путь и перемещение. Мгновенная скорость. Ускорение. Равномерное и равноускоренное движение.
Все формулы школьной физики
Механика кинематика движение по окружности закон всемирного тяготения закон Гука сила трения сила и импульс закон сохранения импульса закон сохранения энергии
Примерные экзаменационные билеты по физике 11 класс
Примерные экзаменационные билеты по физике Билет №1 Механическое движение. Относительность движения. Система отсчета. Материальная точка. Траектория. Путь и перемещение. Мгновенная скорость. Ускорение. Равномерное и равноускоренное движение.
Основные формулы
Электростатика. - закон Кулона. - напряженность электрического поля - принцип суперпозиции полей. - поток через площадку S. - теорема Гаусса. - теорема о циркуляции.
Физик Кулон Шарль Огюстен
Основные годы жизни Шарля Огюстена Кулона. Краткая характеристика научной деятельности ученого, основные заслуги в области военной инженерии и физики, ученые степени и звания, главные его открытия и понятия. Активное участие в жизни Академии наук.
Расчеты электростатического поля
Описание теоремы Гаусса как альтернативной формулировки закона Кулона. Расчеты электростатического поля заданной системы зарядов в вакууме и вычисление напряженности поля вокруг заряженного тела согласно данных условий. Сравнительный анализ решений.
ТОЭ контрольная №5
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра Теоретических основ электротехники
Эфир ХХI века и оригинальное его доказательство
Что же может сказать о «современном» эфире человек, который не связан (и в этом его преимущество) путами традиционной физики? Оказалось, что проблема могла быть разрешена еще в первой половине нашего века.
Хронология открытий в физике электричества
Ученый Открытие 1600 У. Гилберт Заложены основы электро и магнитостатики 1733 Ш. Дюфе Открытие двух видов электричества, установление притяжения разноименных зарядов и отталкивания одноименных
Шаг к структуре пространства
Как часто мы ошибочно полагаем, что в экспериментах вправе сами задавать координаты системы отсчета измеряемых параметров. Иногда это приводит к печальным последствиям.
Электростатическое взаимодействие точечных зарядов
Названное взаимодействие, несмотря на кажущуюся простоту, не удаётся интерпретировать чётко и однозначно. Его можно описать двумя способами: при помощи закона Кулона или, используя полное электростатическое поле зарядов.
Ключ к физике XXI века
Ньютон считал, что гравитация распространяется мгновенно, тяготение сродни электрическому взаимодействию, свет имеет корпускулярную природу, существует абсолютная среда распространения света – эфир, ускорение носит абсолютный характер.
Решение задачи с помощью программ Mathcad и Matlab
Разработка модели движения практически невесомой заряженной частицы в электрическом поле, созданном системой нескольких фиксированных в пространстве заряженных тел. При условии, что тела находятся в одной плоскости, но частица находится вне плоскости.
Решение задачи с помощью программ Mathcad и Matlab
Моделирование движения заряженной частицы, падающей вертикально вниз на одноименно заряженную пластину, с помощью программ Mathcad и Matlab. Построение графика зависимости высоты, на которой находится точка, от времени и скорости движения этой частицы.
Понятия и Законы электростатики
IV правовой курс Понятия и Законы электростатики. выполнил: Скородумов Денис Сергеевич г. Донецк 2002 г. Понятия и Законы электростатики. Электризация –
Новый взгляд на работу сердца и движение крови
Современная нетрадиционная медицина располагает акупунктурным методом диагностики и электрического воздействия на отдельные точки тела. Однако, источник возникновения электрического тока в организме человека до сего времени неизвестен.
![]() обычно обозначают
обычно обозначают ![]() ,
вектор
,
вектор ![]() обозначают
обозначают ![]() . Тогда
напряженность электрического поля и потенциал, создаваемые зарядом, записываются
как:
. Тогда
напряженность электрического поля и потенциал, создаваемые зарядом, записываются
как: ![]() создает
заряд q, находящийся в точке
создает
заряд q, находящийся в точке ![]() .
.![]()
![]() пробегает всевозможные положения из начала координат в точки, где
есть заряд dq. Последний записывается как
пробегает всевозможные положения из начала координат в точки, где
есть заряд dq. Последний записывается как ![]()
![]()
![]() запишется:
запишется: ![]() против оси z естественно из симметрии задачи. Если заряд
положителен, то поле должно быть ориентировано от заряженного сектора, что и
имеет место.
против оси z естественно из симметрии задачи. Если заряд
положителен, то поле должно быть ориентировано от заряженного сектора, что и
имеет место.