Простейшим методом численного интегрирования является метод прямоугольников. Он непосредственно использует замену определенного интеграла интегральной суммой (3.20). В качестве точек ξi могут выбираться левые (ξ = xi-1) или правые (ξi = xi) границы элементарных отрезков. Обозначая f{xi) = yi, ∆xi = hi, получаем следующие формулы метода прямоугольников соответственно для этих двух случаев:
∫ f(x) dx 
h1y0 + h2y1 + ... + hnyn-1 (3.24)
∫ f(x) dx h1y1 + h2y2 + ... + hnyn (3.25)
Широко распространенным и более точным является вид формулы прямоугольников, использующий значения функции в средних точках элементарных отрезков (в полуцелых узлах):
∫ f{x)dx 
, (3.26)
Xi-1/2 = (xi-1 + xi)/2 = xi-1 + hi/2, i = 1,2,... ,n.
В дальнейшем под методом прямоугольников будем понимать последний алгоритм (он еще называется методом средних).
В рассмотренных методах прямоугольников используется кусочно постоянная интерполяция: на каждом элементарном отрезке функция f(x) приближается функцией, принимающей постоянные значения (константой). При этом площадь всей фигуры (криволинейной трапеции) приближенно складывается из площадей элементарных прямоугольников. На рис. 3.2 верхняя, средняя и нижняя горизонтальные штриховые линии относятся к элементарным прямоугольникам, которые соответствуют формулам (3.25), (3.26) и (3.24).
Метод трапеций использует линейную интерполяцию, т. е. график функции у = f(x) представляется в виде ломаной, соединяющей точки (xi, yi). В этом случае площадь всей фигуры приближенно складывается из площадей элементарных прямолинейных трапеций (рис. 3.2). Площадь каждой такой трапеции равна произведению полусуммы оснований на высоту:
σi = 
hi , i=1,2,...,n.
Складывая все эти равенства, получаем формулу трапеций для численного интегрирования:
∫ f{x)dx 
(3.27)
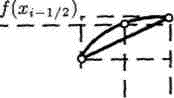
y (xi,yi)
(xi-1,yi-1)
yi-1 yi
hiV
x
xi-1 xi-1/2 xi
Рис. З.2. Вычисление σi в методах
прямоугольников и трапеций
Важным частным случаем рассмотренных формул является их применение при численном интегрировании с постоянным шагом hi = h = const (i = 1,2,...,n). Формулы прямоугольников и трапеций в этом случае принимают соответственно вид
∫ f{x)dx 
, (3.28)
∫ f{x)dx 
( 
+ 
). (3.29)
Погрешность численного интегрирования определяется шагом разбиения. Уменьшая этот шаг, можно добиться большей точности. Правда, увеличивать число точек не всегда возможно. Если функция задана в табличном виде, приходится, как правило, ограничиваться данным множеством точек. Повышение точности может быть в этом случае достигнуто за счет повышения степени используемых интерполяционных многочленов. Рассмотрим два таких способа численного интегрирования: использование квадратичной интерполяции (метод Симпсона) и интерполирование с помощью сплайнов.
Метод Симпсона. Разобьем отрезок интегрирования [а, b] на четное число п равных частей с шагом h. На каждом отрезке [х0,х2], [х2,х4],... , [хi-1,хi+1], ... , [хn-2,xn] подынтегральную функцию f(x) заменим интерполяционным многочленом второй степени:
f(x) 
φi(x) = aix2+bix+ci, xi-1 
x 
xi+1.
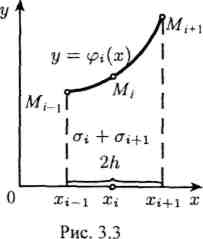
Коэффициенты этих квадратных трехчленов могут быть найдены из условий равенства многочлена в точках хi, соответствующим табличным данным уi. В качестве φi (х) можно принять интерполяционный многочлен Лагранжа второй степени, проходящий через точки Mi-1(xi-1,yi-1), Mi(xi,yi), Mi+1(xi+1, yi+1):
φi(x)= 
yi-1+ 
yi+ 
yi+1.
Сумма элементарных площадей σi и σi+1 (рис. 3.3) может быть вычислена с помощью определенного интеграла. Учитывая равенства xi+1 – xi = xi - xi-1 = h, получаем
σi + σi+1=∫ φi(x)dx=1/2h2∫ 
(x-xi)(x-xi+1)yi-1-2(x-xi-1)(x-x+1)yi+(x-xi-1)(x-xi)yi+1]dx=
= h/3(yi-1+4yi+yi+1)
Проведя такие вычисления для каждого элементарного отреза [хi-1,хi+1], просуммируем полученные выражения:
S = h/3(y0+4y1+2y2+4y3+2y4+...+2yn-2+4yn-1+yn).
Данное выражение для S принимается в качестве значения определенного интеграла:
∫f(x)dx h/3[y0+4(y1+y3+...+yn-1)+2(y2+y4+...+yn-2)+yn]. (3.30)
Полученное соотношение называется формулой Симпсона или формулой парабол.
Эту формулу можно получить и другими способами, например двукратным применением метода трапеций при разбиениях отрезка [а, b] на части с шагами h и 2h или комбинированием формул прямоугольников и трапеций (см. п. 5).
Иногда формулу Симпсона записывают с применением полуцелых индексов. В этом случае число отрезков разбиения п произвольно (не обязательно четно), и формула Симпсона имеет вид
∫ f(x)dx h/6[y0+4(y1/2+y3/2+...+yn-1/2)+2(y1+y2+...+yn-1)+yn]. (3.31)
Легко видеть, что формула (3.31) совпадет с (3.30), если формулу (3.30) применить для числа отрезков разбиения 2п и шага h/2.
Пример. Вычислить по методу Симпсона интеграл I =∫ 
.
Значения функции при п = 10, h = 0.1 приведены в табл. 3.3.
Применяя формулу (3.30), находим
I=0.1/3[y0+4(y1+y3+y5+y7+y9)+2(y2+y4+y6+y8)+y10]=...=0.785398.
Результат численного интегрирования с использованием метода Симпсона оказался совпадающим с точным значением (шесть значащих цифр).
Один из возможных алгоритмов вычисления определенного интеграла по методу Симпсона представлен на рис. 3.4. В качестве исходных данных задаются границы отрезка интегрирования [а, b], погрешность ε, а также формула для вычисления значений подынтегральной функции у = f(х). Первоначально отрезок [а, b] разбивается на две части с шагом h = (b — а)/2. Вычисляется значение интеграла 11. Потом число шагов удваивается, вычисляется значение 12 с шагом h/2. Условие окончание счета принимается в виде | I1 —12 | < е. Если это условие не выполнено, происходит новое деление шага пополам и т. д.
Отметим, что представленный на рис. 3.4 алгоритм не является оптимальным: при вычислении каждого приближения I2 не используются значения функции f(х), уже найденные на предыдущем этапе.
5