


Зміст.
Вступ…………….……………………………………………….2
Розділ І. Історія виникнення проблеми ірраціонального числа…………………….8
Розвіл ІІ. Дійсні числа.
§1. Множина раціональних чисел …………..15
§2. Дві основні задачі, які приводять до розширення множини раціональних чисел……….23
§3. Множина дійсних чисел…………………..28
§4. Модуль дійсного числа і його властивості……………………………………………..32
§5. Наближені значення дійсних чисел……………………………………………………..38
Розділ ІІІ. Методика викладання даної теми в школі…..……………………………………41
Висновки………………….…………………………….53
Література………………………………………………55
Додаток………………………………………………….56
Вступ.
Математика вивчає просторові форми і кількісні відношення. Візьмемо, наприклад, який-небудь предмет. Нас може цікавити, яка його густина, міцність, теплопровідність. Відповіді на подібні запитання дає фізика. На запитання: З якої речовини цей предмет? Як на нього діють кислоти, луги? Чи може він горіти?- відповіді дає хімія. Але нас може цікавити й таке: Яка форма цього предмета? Які його розміри? Ці питання розглядаються в математиці.
Математика як наука сформувалася в Стародавній Греції в VII-III столітті до нашої ери, коли Фалес, Піфагор, Евклід та інші вченні систематизували відомі на той час математичні знання і виклали їх з точним обгрунтуванням. Тоді ж виникло і слово “математика”, яке в перекладі з грецької означає “знання”, “наука”.
Тепер математика потрібна всім. Без математичних обчислень не можна побудувати не тільки космічного корабля, електростанції, підводного човна, а й звичайного будинку. Від того, як зроблено попередні розрахунки, залежать вартість об’єкта, його якість і терміни спорудження. Важко знайти таку галузь людської діяльності, де можна було б обійтися без математики, причому з часом діапазон її практичних застосувань розширюється. Нині математичні методи проникли навіть у медицину, історію, лінгвістику та інші науки.
Збільшується не тільки кількість наук, які вже не можуть обходитись без математики, а й обсяг математичних знань, що застосовуються цими науками. Ось чому так важливо, щоб наша молодь мала грунтовну математичну підготовку.
Коротко мету викладання математики в загальноосвітній школі можна визначити так. Шкільний курс математики має забезпечити міцне і свідоме оволодіння системою математичних знань, умінь і навичок, які потрібні для загального розвитку учнів, для їх практичної діяльності в умовах сучасного виробництва, для вивчення на достатньо високому рівні споріднених шкільних предметів (фізики, креслення, хімії тощо ) і для продовження освіти.
Із сказаного випливає, що викладання математики в наших школах повинно відповідати загальноосвітнім, практичним і виховним цілям.
Вивчення математики може також сприяти вихованню почуття патріотизму. Учням треба показати, що в розвиток математики внесли великий вклад і відомі всьому світові українські математики – М.В.Остроградський, Г.Ф.Вороний, М.Ф.Кравчук та ін., російські вчені – М.І.Лобачевський, П.Л.Чебишов, С.В.Ковалевська, О.М.Ляпунов та ін. Ми по праву можемо пишатися нашими математиками! Насамперед такими, як М.М.Боголюбов. І.М,Виноградов, В.М.Глушков, А.М.Колмогоров, Г.П.Бевз та ін.
У процесі навчання математики є можливість виховувати в учнів акуратність, увагу, культуру письма і усної мови тощо.
Методика викладання математики – це наука про різні способи і форми передачі учням математичних знань, про мету, зміст і засоби навчання і нерозривно пов’язані з ними питання виховання учнів у процесі викладання математики. Вона належить до циклу педагогічних наук. До XVIII століття всі питання навчання в школі розглядалися в педагогіці. Але пізніше педагогіка дуже розширилася, диференціювалась і з неї виділились методики викладання окремих навчальних предметів, у тому числі й методика викладання математики або, коротше, методика математики.
Першою книгою з методики математики вважається видана в 1803 році книга Песталоцці “Наочне вчення про число”.
Назву “методика математики” запропонував у 1836 році Дістервег.
Перед методикою викладання математики стоять такі основні завдання:
1) визначити мету навчання математики для різних типів шкіл і вікових груп учнів;
2) для кожної з цих груп конкретизувати зміст навчання математики ( які теми, в якому обсязі і на якому рівні опрацьовувати);
3) відібрати методи, форми і засоби навчання математики, придатні для тих чи інших тем і умов;
4) показати, як слід виховувати і розвивати учнів в процесі навчання математики.
Коротше кажучи, методика викладання математики покликана дати відповіді на такі запитання: 1) навіщо навчати? 2) чому навчати? 3) як навчати? 4) як виховувати і розвивати учнів, навчаючи математики?
Як і всі інші науки, методика викладання математики має свій об’єкт дослідження, свої проблеми, свою історію. Вона потрібна багатьом, за її розвитком стежать сотні тисяч учителів математики.
У ШКМ розглядається одна з провідних ліній розвитку –вчення про число. В науці існує теорія чисел, але вона складна і не розглядається в школі. Але оскільки числа утворюють базис математики, то важливим є засвоєння основних елементів цієї теорії в шкільному курсі. Однією з тем даної теорії є “дійсне число”. За шкільною програмою на її вивчення відводиться 2 години, що є дуже мало. Тому від вчителя вимагається велика професійна підготовка для пояснення цього матеріалу, глибокі знання методики викладання його: оскільки вчитель повинен систематизувати вже набуті знання учнів, ввести нові поняття, пояснити їх зрозуміло для учнів і закріпити новий матеріал.
В кінці уроку, учень повинен впевнено відповідати на такі питання: що таке ірраціональне число? Що означає число 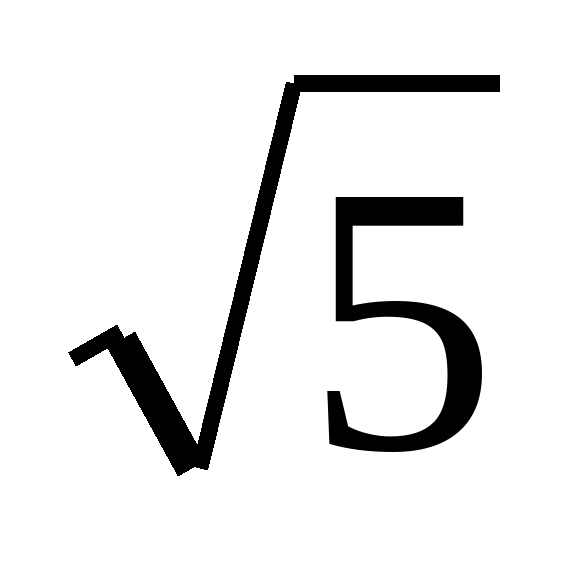 ? Яким чином можна уявити множину дійсних чисел?
? Яким чином можна уявити множину дійсних чисел?
Для чого це треба? Дуже часто вчителі стикаються з такою проблемою, що старшокласники не можуть розкрити зміст ірраціонального числа, і це гальмує запланований процес роботи. Вважаючи, що всі числа – елементарність, насправді, учні з часом стикаються з незнанням так званого елементарного. Надолужувати втрачене, вчитель іноді не має часу, тому в знаннях учнів залишаються недоліки, які виправляються лише при бажанні самого школяра вивчити те, чого не знає.
В цій роботі я досліджуватиму, як краще викладати тему “Дійсне число”, щоб учні оволоділи системою знань з цього матеріалу, вмінням і навичками, які потрібні їм для загального розвитку, для їх практичної діяльності.
РОЗДІЛ І. Історія виникнення проблеми ірраціонального числа.
Сукупність раціональних чисел немає властивості неперервності. Тому вона виявилась недостатньою при вивченні величин, які змінюються неперервно. Виникла потреба в розширенні поняття числа, яка полягає в переході від множини раціональних чисел до множини дійсних чисел. Цей перехід полягає в приєднанні до раціональних чисел так званих ірраціональних чисел, які виражаються через раціональні лиш наближено.
Ірраціональні числа виникли пізніше від раціональних і їх довго не визнавали за числа як такі; називали то “несумірними”, то “невиразними”, то “супротивними щодо розуму”.
Ще стародавні греки відкрили в геометрії існування несумірних відрізків. Це відкриття було поворотним пунктом в історії античної математики. Важко переоцінити значення цього відкриття. Ми не знаємо точно дослідження яких питань привело до відкриття несумірності. Це могло статися:
1).в геометрії при знаходженні спільної міри сторони і діагоналі квадрата;
2).в арифметиці могло виникнути питання про точне визначення такого дробу, квадрат якого дорівнює два.
Як би там не було мова йшла про відшукання і дослідження величини, яку ми тепер позначаємо 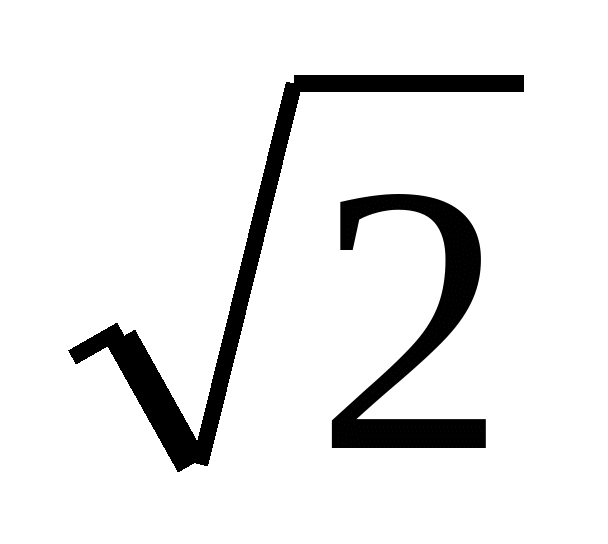 .
.
Відкриття факту, що між двома відрізками—стороною і діагоналлю квадрата не існує спільної, хоч як завгодно малої, міри, привело до справжньої кризи основ грецької математики.
Піфагорійці, які відкрили існування несумірних відрізків, тримали це відкриття в таємниці, бо воно суперечило їх ідеалістичному вченню про гармонію чисел у навколишньому світі; не можна було визнавати справжнім їх учення про цілочисельну основу всього існуючого, у тому числі й геометричних величин.
“Піфагорійці пов’язували вічну душу з вічними формами числа, приписуючи цю властивість зокрема числу 10=1+2+3+4. Увесь світ, за їх ученням, складався з чистих чисел. Ця форма крайнього ідеалізму проявляється у Святій Трійці, чотирьох євангелістах, семи смертних гріхах тощо.
Відкриття несумірності діагоналі квадрата з його стороною нанесло серйозний удар по всій піфагорійській школі і сприяло її розпаду.
Незабаром було встановлено, що несумірність діагоналі і сторони квадрата не є винятком, що існують й інші величини, відношення яких не можна подати відношенням двох (цілих) чисел. Феодор з Кірени (Vст.до н.е.) показав, що сторони квадратів, площі яких лорівнюють 3, 5, 6, 7,…, 17, несумірні з стороною одиничного квадрата.
Замість того, щоб розширити поняття числа, греки дійшли висновку, що треба відокремити вивчення цілих чисел від геометрії; встановлюється точна межа між арифметикою і геометрією.
Усі ірраціональності, до яких ведуть розв'язування квадратних рівнянь, Евклід побудував суто геометрично. Відомо “задача про подвоєння куба” привела греків до ірраціональностей вищого порядку; цю задачу вони розв'язали також геометрично і за допомогою побудови довели існування несумірних відрізків вищого порядку.
Відкриттю несумірних величин надавали важливого значення ще в старовину. Так, видатний старогрецький філософ Арістотель (384-322р.р.дон.е.) вказував, що воно викликало здивування, як і всяке справжнє наукове відкриття.
Факт існування несумірних відрізків не гальмував розвитку геометрії. Греки розробили теорію відношень відрізків, яка враховувала можливість їх несумірності; вони вміли порівнювати такі відношення за величиною, виконувати над ними арифметичні дії (в суто геометричній формі), інакше кажучи, користувалися такими відношеннями як числами.
Щоб позбутися ірраціональних чисел, греки вживали їх наближення, досить точні для практичних обчислень. В Архімеда ці наближення мали науковий характер. І хоч Герон Олександрійський при обчисленні площ добуває квадратний корінь з добутку чисел, а Діофант Олександрійський говорить уже про числа нераціональні, однак, ідея про те, що відношеня довжин несумірних відрізків можна розглядати як число, в грецькій математиці не була усвідомлена до кінця.
Отже: можна сказати, що у вирішенні проблеми в галузі розширення поняття про число греки майже нічого не зробили. Як для Евкліда, так і, по суті, для Діофанта існувало тільки ціле число.
Індійці і араби розглядали ірраціональні числа як числа нового виду. Вони не задумувались над тим, чи законно додавати, перемножувати, ділити ірраціональні числа. Так, наприклад, Бхаскара знищує ірраціональніcть у знаменнику, множачи чисельник і знаменник на той самий ірраціональний множник.
Термін “ірраціональний” у математичному розумінні вперше застосував у XIV ст.англійський математик Брадвардін (близько 1290-1349). Поняття числа з цим терміном пов’язує вперше (1544) німецький математик Штіфель. Але й він під час введення дій над ірраціональними числами вдається, як і Евклід, до відрізків.
Таким міркуванням властива загальна риса – ірраціональні числа не вважали повноправними числами. Але ці числа треба було розглядати, вивчати, бо зокрема, обчислюючи ірраціональні корені алгебраїчних рівнянь і логарифми чисел, визначаючи значення тригонометричних функцій і т.д., доводилося шукати їх достатні раціональні наближення і, по суті, оперувати ними як числами.
Велике значення для розвитку поняття ірраціонального числа мали праці Стевіна. Він був першим математиком, який повністю підтримував точку зору визнання повної рівноправності раціональних та ірраціональних чисел, однак, останні почали застосовувати разом з від’ємними числами тільки після появи геометрії Декарта (1637).
Ідея Декарта привела до узагальнення поняття про число. Між точками прямої і числами було встановлено взаємно однозначну відповідність. У математику була введена змінна величина.
До початку XVIII ст. сформувалися три тлумачення поняття ірраціональної величини:
1).ірраціональне число розглядали як корінь n-го степеня з цілого або дробового числа, коли результат добування кореня не можна виразити “точно” цілим або дробовим числом (найдавніше);
2).ірраціональне число трактували як межу, до якої його раціональні наближення можуть підійти як завгодно близько (це тлумачення йде від Стевіна і Валліса);
3).число розглядали як відношення однієї величини до другої величини такого самого роду, взятої за одиницю; коли величина несумірна з одиницею, число називали ірраціональним (Ньютон, Декарт).
Два останні означення ірраціонального числа довго не поширювались. Математики найчастіше трималися першого означення і говорили не про ірраціональні числа, а про ірраціональні величини. Тільки найпередовіші математики кінця XVII і початку XVIII ст.—Ньютон , Лейбніц та інші—вважали поняття ірраціонального числа об’єктивним, трактували його по-новому і широко застосовували в математиці.
У другій половині XVIIIст., у зв’язку з дальшим розвитком механіки і математики, об’єктивність поняття ірраціонального числа набуває ширшого визнання. Третє означення ірраціонального числа стає на перше місце і повсюдно проникає в літературу. Водночас дещо розвивається і друге тлумачення поняття ірраціонального числа. Так, Ейлер, Ламберт та інші вчені встановили, що нескінченний періодичний дріб завжди є раціональним числом. Тому ірраціональне число є нескінченним неперіодичним дробом. Однак аж до другої половини XIXст.не було розроблено загальної теорії ірраціональних чисел.
Остаточного розвитку теорія ірраціональних чисел набула тільки в другій половині XIXст.у працях німецьких математиків Дедекінда, Кантора і Вейєрштрасса.
РОЗДІЛ ІІ. “Дійсні числа”
§1. Множина раціональних чисел
Учні 8-го класу часто зустрічали крім раціональних чисел ще й числа іншої природи – до них часто приводить операція добування квадратного кореня (і не тільки вона). Отже, треба більш досконало познайомитися з новими числами. Але для цього доцільно було б систематизувати знання учнів про вже відомі, тобто раціональні, числа.
1.1. Деякі символи математичної мови.
Учням добре відомі натуральні числа:
1, 2, 3, 4, …
Множина всіх натуральних чисел позначається буквою N.
Якщо до натуральних чисел приєднати число 0 і всі цілі від’ємні числа:
-1, -2, -3, -4,…
то одержиться множина цілих чисел. Цю множину позначають буквою Z.
якщо до множини цілих чисел приєднати всі дробові числа:
2/3, 15/8, -33/58,…
то одержиться множина раціональних чисел. Цю множину позначають буквою Q.
Будь-яке ціле число m можна записати у вигляді дробу m/1, тому можна твердити, що
Множина Q раціональних чисел—це множина, яка складається із чисел виду m/n, -m/n (де m,n – натуральні числа) і числа 0.
Використовуючи введені позначення N,Z,Q бажано ввести наступне:
замість “n –натуральне число “ можна писати nєN(і читатиметься: “елемент n належить множині N”). Математичний символ є називають знаком належності; аналогічно записують mєZ (“m – ціле”), rєQ (“r – раціональне число”). Зрозуміло, що N – частина множини Z, а Z – частина множини Q. Для зображення даної ситуації в математиці також є спеціальне позначення:
N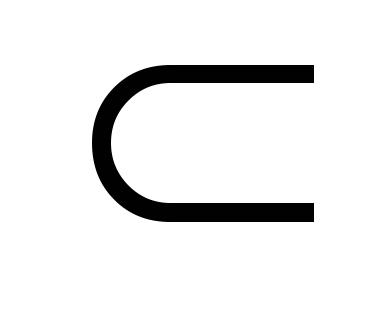 Z, Z
Z, Z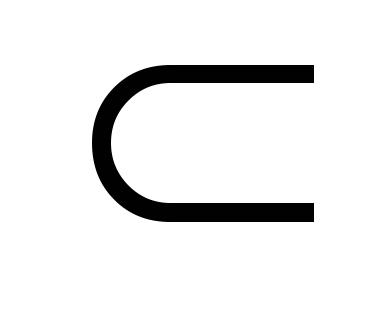 Q
Q
Математичний символ 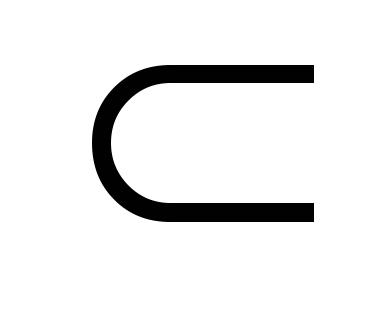 називають знаком включення (однієї множини в іншу).
називають знаком включення (однієї множини в іншу).
Взагалі, в математиці запис хєХ позначає те, що х—один з елементів множини Х. Запис А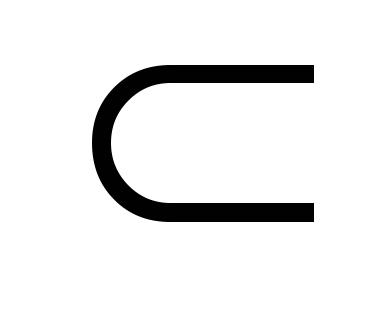 В означає, що множина А є частиною множиниВ. Математики частіше кажуть: А—підмножина множини В.
В означає, що множина А є частиною множиниВ. Математики частіше кажуть: А—підмножина множини В.
Потрібно звернути увагу учнів на те, що множини в математиці позначають великими літерами, а елементи множин—маленькими .
А також звернути увагу на те, що знаки належності і включення—різні, відповідно 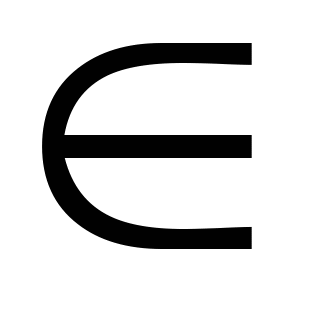 і
і 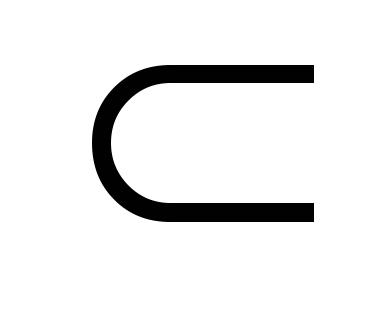 .
.
Для того щоб записати, що елемент х не належить множині Х або що множина А не є підмножиною множини В, використовують ті ж символи, але перекреслені: х 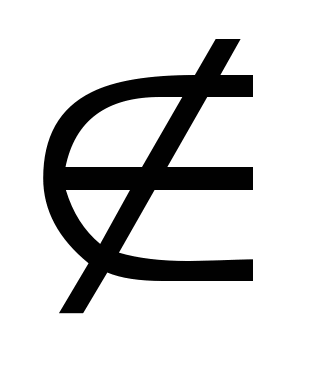 Х, А
Х, А  В.
В.
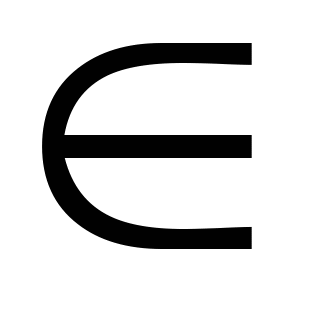 N, 5
N, 5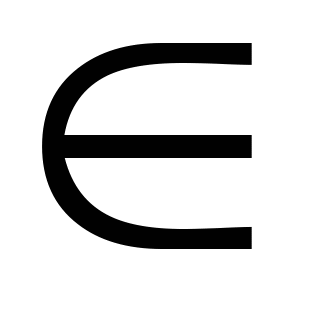 Z, 5
Z, 5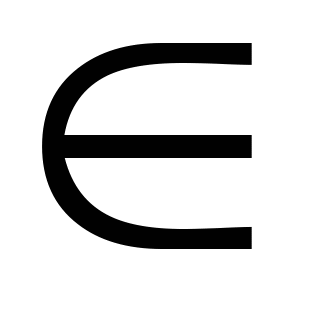 Q; Б) -7
Q; Б) -7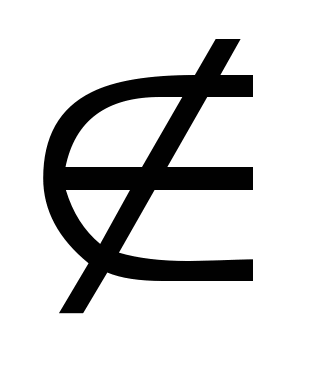 N, -7
N, -7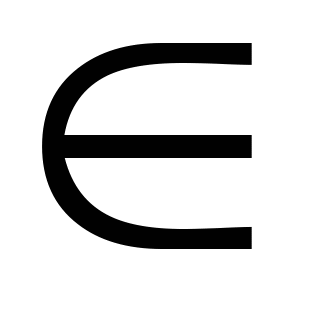 Z, -7
Z, -7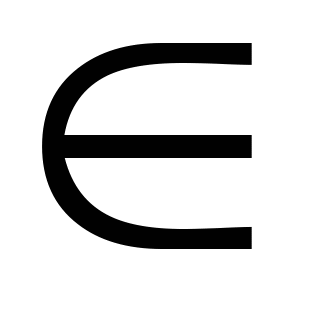 Q; B) 3,5
Q; B) 3,5 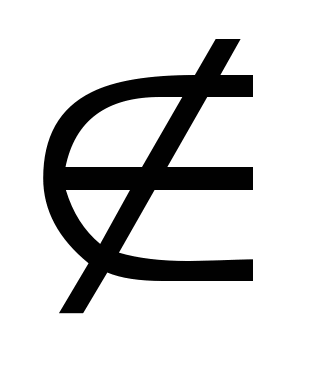 N, 3,5
N, 3,5 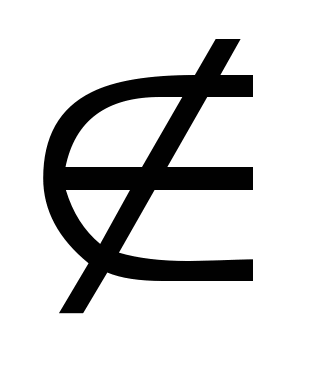 Z, 3,5
Z, 3,5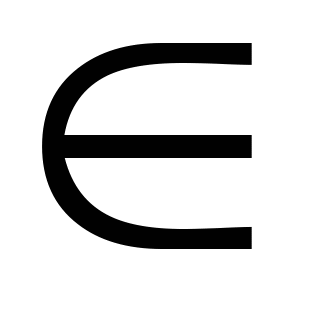 Q; Г)
Q; Г) 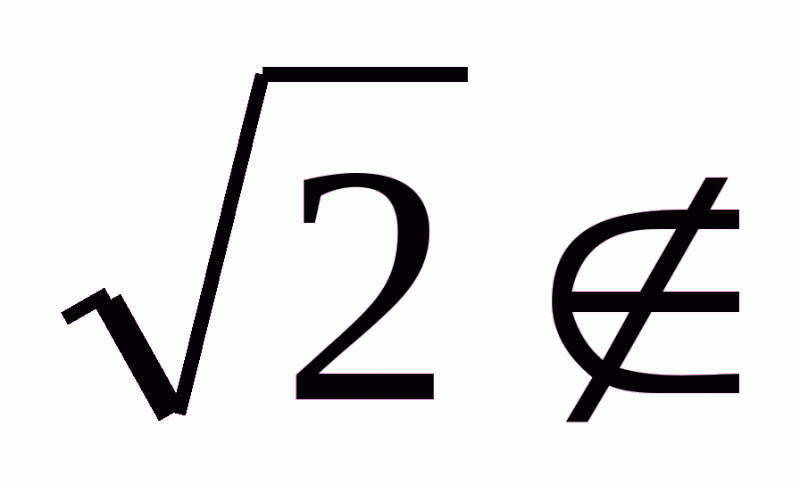 N,
N, 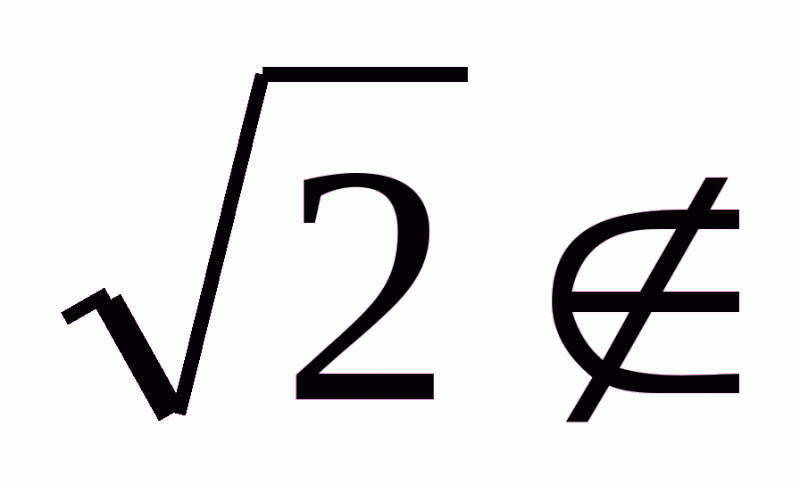 Z,
Z, 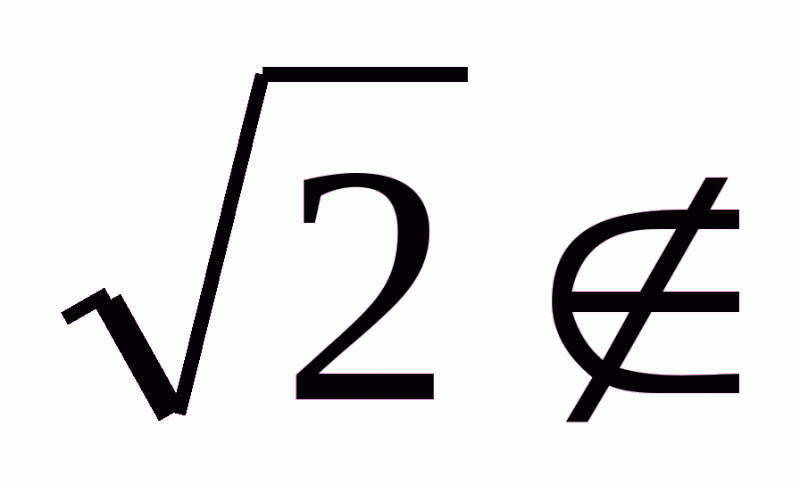 Q;
Q; Приклад 2.
2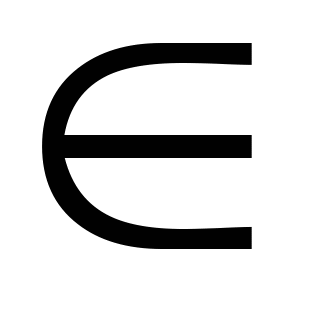 [1,3]; 1
[1,3]; 1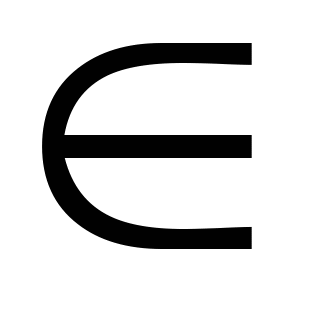 [1,3]; 1
[1,3]; 1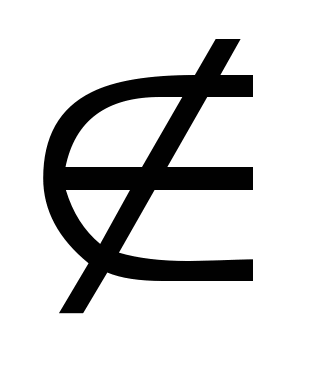 (1,3).
(1,3).
Приклад 3.
А) N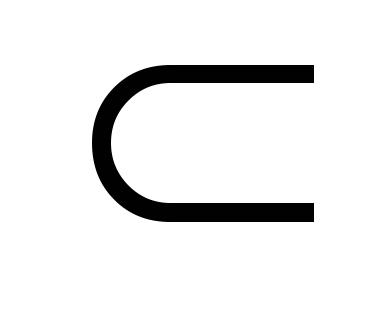 Z, Z
Z, Z N, Z
N, Z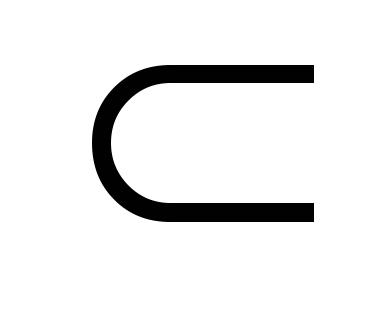 Q, Q
Q, Q Z;
Z;
Б) (1,3)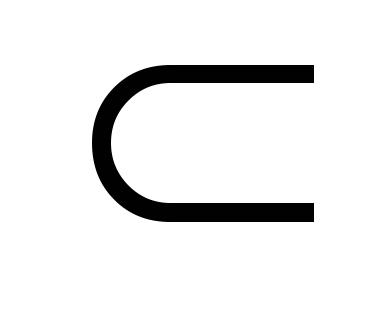 [1,3], [1,3]
[1,3], [1,3] (1,3),[1,3]
(1,3),[1,3]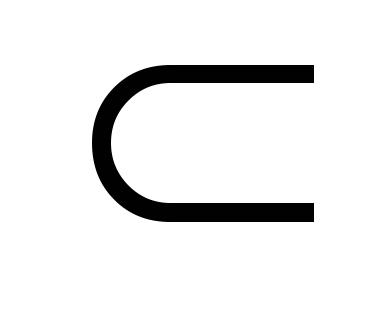 (0,+∞),[2,5]
(0,+∞),[2,5]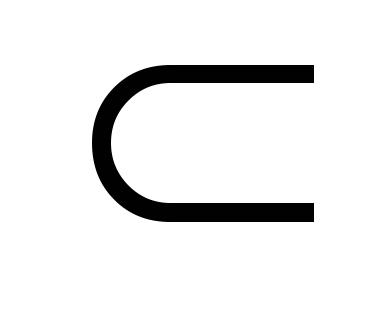 (3,8).
(3,8).
1.2. Раціональні числа як нескінченні десяткові періодичні дроби.
До раціональних чисел, як вже не раз підкреслювалось, відносяться всі ті числа, з якими учні успішно оперували до тих пір,поки не зустрілись з квадратними коренями. Це були цілі числа, звичайні дроби і десяткові дроби. Для всіх цих чисел використовується один і той же спосіб запису, який би доцільно обговорити.
Розглянемо, наприклад, ціле число 5, звичайний дріб 7/22 і десятковий дріб 8,377. Ціле число 5 можна записати у вигляді нескінченного десяткового дробу: 5,00000… Десятковий дріб 8,377 також можна записати у вигляді нескінченного десяткового дробу: 8.3770000… Для числа 7/22 використаємо метод “ділення кутом”:
7,000000… 22
-66 0,31818…
40
-22
180
-176
40
-22
180
…
Звідси видно, що починаючи з другої цифри після коми, відбувається повторення однієї і тієї ж групи цифр: 18, 18, 18,… Таким чином, 7/22=0,3181818… Скорочено це записують так: 0.3(18)
Група цифр після коми, яка повторюється, називається періодом, а сам десятковий дріб—нескінченним десятковим періодичним дробом.
Між іншим, і число 5 можна подати у вигляді нескінченного періодичного дробу. Для цього треба в періоді записати число 0:
5=5,00000…=5,(0).
Аналогічно число 8,377:
8,377=8,377000…=8,377(0)
Щоб все було акуратно, кажуть так: 8,377—скінченний десятковий дріб, а 8,377000…-- нескінченний десятковий дріб.
Таким чином, і число 5, і число 7/22, і число 8,377 вдалося записати у вигляді нескінченного періодичного десяткового дробу.
Взагалі, будь-яке раціональне число можна подати у вигляді нескінченного періодичного десяткового дробу.
Зауваження.
Це пояснення зручне для теорії, але не дуже зручне для практики. Адже, якщо дано скінченний десятковий дріб 8,377, то для чого потрібний його запис у вигляді 8.377(0)? Тому кажуть так:
Будь-яке раціональне число можна записати у вигляді скінченного десяткового дробу або у вигляді нескінченного періодичного десяткового дробу.
Вище було показано, як звичайний дріб подають у вигляді нескінченного періодичного десяткового дробу. Справедливе і обернене: будь-який нескінченний десятковий періодичний дріб можна подати у вигляді звичайного дробу. Це означає, що будь-який нескінченний періодичний десятковий дріб є раціональне число.
Потрібно показати на прикладі, як нескінченний періодичний десятковий дріб перетворюють в звичайний дріб.
Приклад. Записати у вигляді звичайного дробу нескінченний періодичний десятковий дріб:а)1,(23); б)1,5(23).
Розв'язання
А) нехай х=1.(23), тобто х=1,232323… Домножимо х на таке число, щоб кома перенеслася вправо рівно на один період. Оскільки в періоді є дві цифри, то число х помножимо на 100. Отримаємо:
_ 100х=123.232323…
і х=1,232323…
100х-х=123,232323…-1,232323…,
99х=122
звідки знаходимо х=122/99
Отже, 1,(23)=122/99.
Б) Нехай х=1.5(23)=1,5232323…Спочатку помножимо х на 10, щоб в отриманому добутку період починався після коми: 10х=15,232323… Тепер число 10х помножимо на100—тоді кома перенесеться рівно на один період вправо: 1000х=1523.2323… Маємо
1000х=1523.232323…
10х=15,232323…
990х=1508; х=1508/990=754/495.
Відповідь: а) 1,(23)=122/99; б)1,5(23)=754/495.
Тепер узагальнимо все вище сказане:
Множину Q раціональних чисел можна розглядати як множину чисел виду m/n, де m—ціле число,n—натуральне число, або як множину нескінченних періодичних десяткових дробів.
§2. Дві основні задачі, які приводять до розширення множини раціональних чисел.
2.1. Дві основні теореми для розширення множини раціональних чисел.
Вже неодноразово відмічалося, що не всі числа, з якими доводиться зустрічатися в реальному житті, є раціональними. Так, не є раціональним числом довжина гіпотенузи прямокутного трикутника з катетами 1см і 2см: дійсно, довжина с і довжини катетів пов’язані теоремою Піфагора: с2=12+22, тобто с= см, а
см, а  -- не раціональне число. Корені рівняння х2=7 також не раціональні числа—це числа
-- не раціональне число. Корені рівняння х2=7 також не раціональні числа—це числа 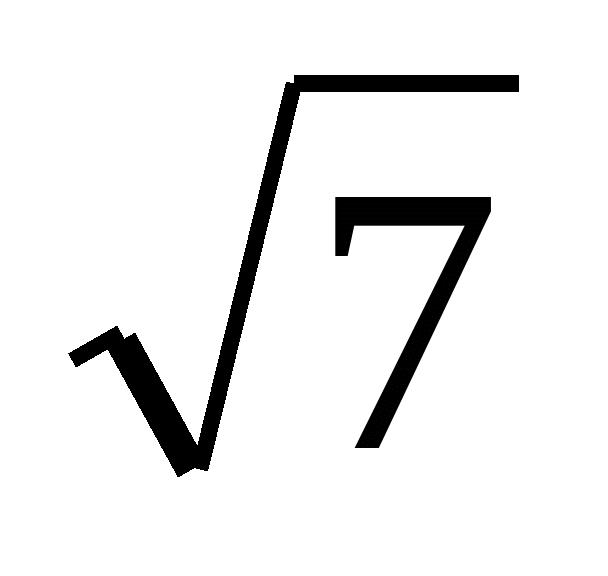 і -
і -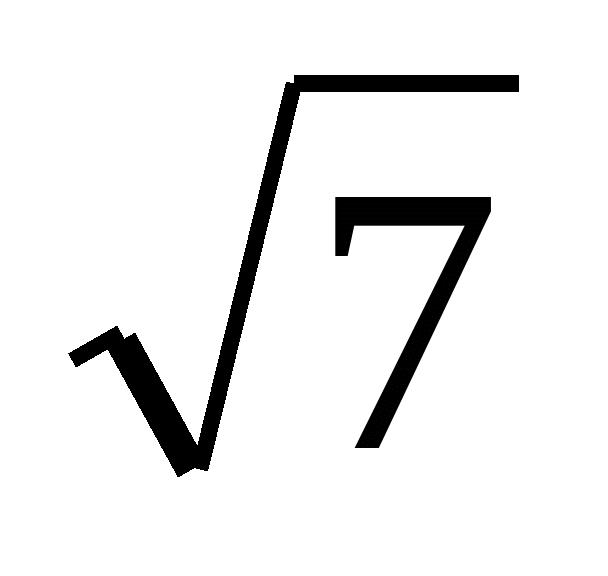 . Щож це за числа, що не є раціональними?
. Щож це за числа, що не є раціональними?
Перш за все необхідно відмітити, що в математиці не заведено говорити “нераціональне число”, бо використовують поняття ірраціональне число. Терміни “раціональне число”, “ірраціональне число” походять від латинського слова ratio—“розум” (дослівний переклад:”раціональне число – розумне число”, “ірраціональне число—нерозумне число “; взагалі, так кажуть і в реальному житті: “він вчинив раціонально”—це означає, що він вчинив розумно; “так діяти нераціонально”—це означає, що так діяти нерозумно).
Ці висновки, які були зроблені інтуїтивно, з часом були науково підтверджені. Були виділені, як основні, дві задачі, які учнями вивчаються у вигляді теорем.
Теорема. Не існує такого раціонального дробу p/q (де p і q—натуральні числа), квадрат якого був би рівний 2.
Доведення. (методом від супротивного). Нехай існує такий дріб p/q, що (p/q)2=2. Будемо вважати, що дріб p/q нескоротний, тобто p і q немають спільних множників. Так як p2=2q2, то звідси видно, що р- парне число : р=2r (де r-ціле число ) і тому q-непарне. Підставляючи замість р його вираз, знайдемо q2=2r2. Звідси видно, що q-парне число. Отримане протиріччя і доводить теорему.
Теорема. Сторона квадрата несумірна з його діагоналлю.
Доведення. Справді. Нехай сторона квадрата дорівнює 1. Припустимо, що довжина діагоналі такого квадрата визначається раціональним числом виду p/q, де p і q- натуральні числа. Дріб p/q вважатимемо нескоротним. Тоді згідно теореми Піфагора одержимо (p/q)2=2 або р2=2q2. Тоді аналогічно попередньої теореми доводимо, що довжина діагоналі квадрата, сторона якого 1, не виражається раціональним числом.
У цьому випадку кажуть, що діагональ квадрата є несумірною з його стороною.
Числа, які задовольняють умови цих теорем називають ірраціональними.
Тепер ставиться задача розширити множину раціональних чисел, приєднавши до них числа нового роду—ірраціональні. Ця розширена область утворює множину дійсних чисел. Разом з тим покажемо, що в цій області залишаються справедливими всі властивості раціональних чисел, до яких відносяться арифметичні дії і порівняння чисел з допомогою знаків нерівності.
2.2. Ірраціональне число як нескінченний неперіодичний десятковий дріб.
Розглянемо ірраціональне число  . Очевидно, що воно міститься між числами 2 і 3; а якщо точніше, то між числами 2,2 і 2,3; якщо ще більш точніше, то між числами 2,23 і 2,24. Можна продовжити уточнення оцінок числа
. Очевидно, що воно міститься між числами 2 і 3; а якщо точніше, то між числами 2,2 і 2,3; якщо ще більш точніше, то між числами 2,23 і 2,24. Можна продовжити уточнення оцінок числа  і визначити межі для третього десяткового знаку після коми. Одержимо 2,2362=4,999696, що менше 5; 2,2372=5,004167, що більше 5. Отже, 2,236
і визначити межі для третього десяткового знаку після коми. Одержимо 2,2362=4,999696, що менше 5; 2,2372=5,004167, що більше 5. Отже, 2,236 <
< <2.237.
<2.237.
Аналогічно можна з’ясувати межі для четвертого знаку після коми, для п’ятого знаку іт.д. Зрозуміло, що наближене значення виконується 
 2,236. Якщо ж вважати. Що для числа
2,236. Якщо ж вважати. Що для числа  виписані всі наступні десяткові знаки, то:
виписані всі наступні десяткові знаки, то:  =2,236… Це—нескінченний десятковий дріб. Вище ми розглядали нескінченні десяткові дроби, але вони були періодичні і вони виражали раціональні числа. Тільки що ми з’ясували, що ірраціональним числом називають нескінченний неперіодичний дріб.
=2,236… Це—нескінченний десятковий дріб. Вище ми розглядали нескінченні десяткові дроби, але вони були періодичні і вони виражали раціональні числа. Тільки що ми з’ясували, що ірраціональним числом називають нескінченний неперіодичний дріб.
Розглянемо один цікавий приклад. Якщо довжину будь-якого кола поділити на його діаметр, то одержиться ірраціональне число 3,141592… Цей факт був встановлений в ІІІст.дон.е.грецьким математиком і філософом Архімедом. Для цього числа в математиці введене спеціальне позначення π.
Будь-яка арифметична операція над раціональними числами зводиться в результаті до раціонального числа. А про ірраціональні числа нічого такого впевнено сказати неможна. Наприклад:  - ірраціональне число , а
- ірраціональне число , а 
 =5—раціональне число , а якщо
=5—раціональне число , а якщо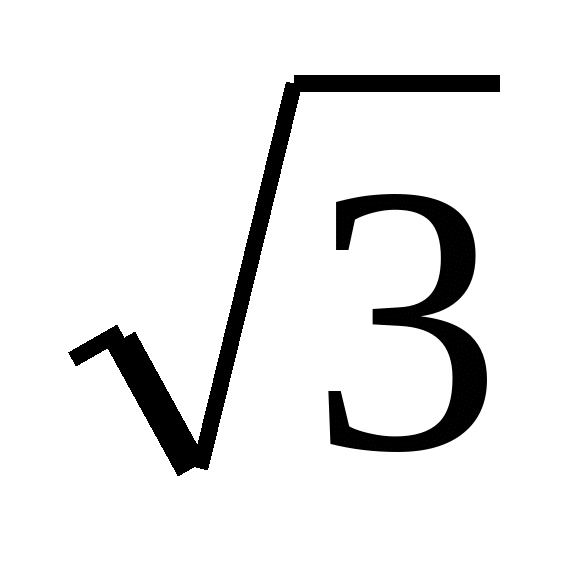
 =
=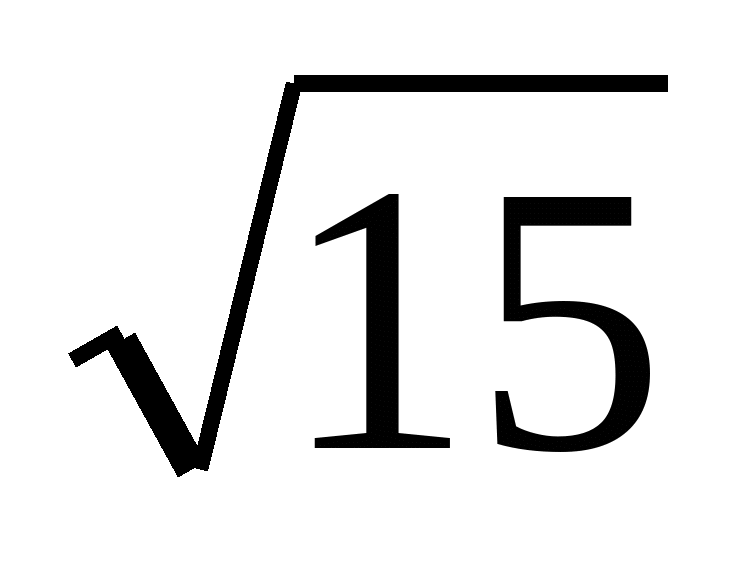 -- ірраціональне число , причому
-- ірраціональне число , причому 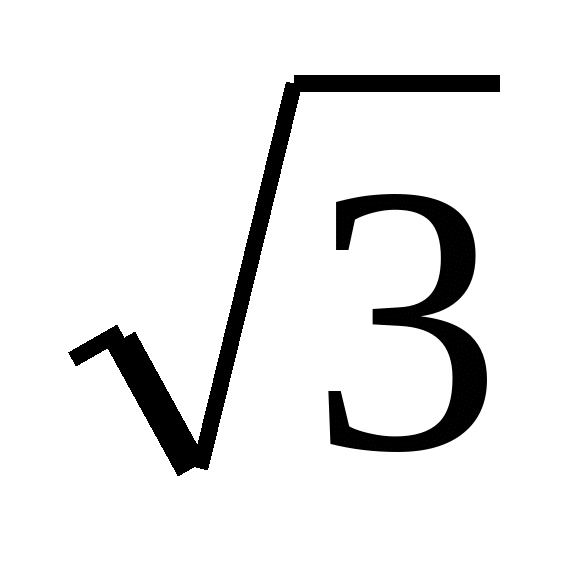 -ірраціональне число. Все це стосується і інших операцій.
-ірраціональне число. Все це стосується і інших операцій.
Цікаво, а якщо в операції приймають участь одне раціональне і одне ірраціональне числа, яке з них “пересилить”? як з’ясувалося “пересилить” ірраціональне число. Розглянемо приклад: дано раціональне число 3 і ірраціональне  ; складемо суму 3+
; складемо суму 3+ . Нехай це є раціональне число р, тобто 3+
. Нехай це є раціональне число р, тобто 3+ =р. Тоді
=р. Тоді  =р-3, а р-3 є раціональним числом. Отримали, що
=р-3, а р-3 є раціональним числом. Отримали, що  - раціональне число, а це не вірно. Одержали протиріччя, отже, зроблене нами припущення неправильне, тобто 3+
- раціональне число, а це не вірно. Одержали протиріччя, отже, зроблене нами припущення неправильне, тобто 3+ -ірраціональне число. Аналогічно можна показати, щоі різниця є число ірраціональне. Якщо ці числа додати, то (3+
-ірраціональне число. Аналогічно можна показати, щоі різниця є число ірраціональне. Якщо ці числа додати, то (3+ )+(3-
)+(3- )=6—раціональне число.
)=6—раціональне число.
Висновок.
1. Будь-яка арифметична операція над раціональними числами в результаті приводить до раціональних чисел.
2. Арифметичні дії над ірраціональними числами в результаті може привести як до раціональних так і до ірраціональних чисел.
3. Якщо дія виконується над раціональним та ірраціональним числами, то одержимо—ірраціональне число .
§3. Множина дійсних чисел.
Якщо множину раціональних чисел доповнити множиною ірраціональних чисел, то разом вони складають множину дійсних чисел. Цю множину позначають літерою R; використовують також символічний запис (- ;+
;+ ).
).
Множину дійсних чисел можна описати таким чином: це множина скінченних і нескінченних дробів.
Кожне дійсне число можна зобразити точкою на координатній прямій, і навпаки, кожна точка координатної прямої має дійсну координату. Математично про це говорять так: між множиною дійсних чисел і множиною точок координатної прямої встановлено взаємно однозначну відповідність. Координатна пряма є геометрична модель множини дійсних чисел, тому координатну пряму часто називають числовою прямою.
Доцільно звернути увагу на те, що координатною прямою учні користувалися, починаючи з 5-го класу. Тепер очевидно, що в їх знаннях був недолік: не для будь-якої точки вони змогли б знайти координату.
Розглянемо приклад. Дана, координатна пряма, на її одиничному відрізку побудований квадрат, діагональ квадрата ОВ в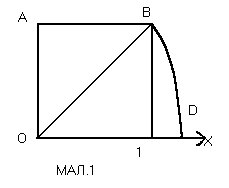 ідкладена на координатній прямій від точки О вправо, одержали точку D (мал.1). Яка координата точки D? вона дорівнює довжині діагоналі квадрата, тобто
ідкладена на координатній прямій від точки О вправо, одержали точку D (мал.1). Яка координата точки D? вона дорівнює довжині діагоналі квадрата, тобто 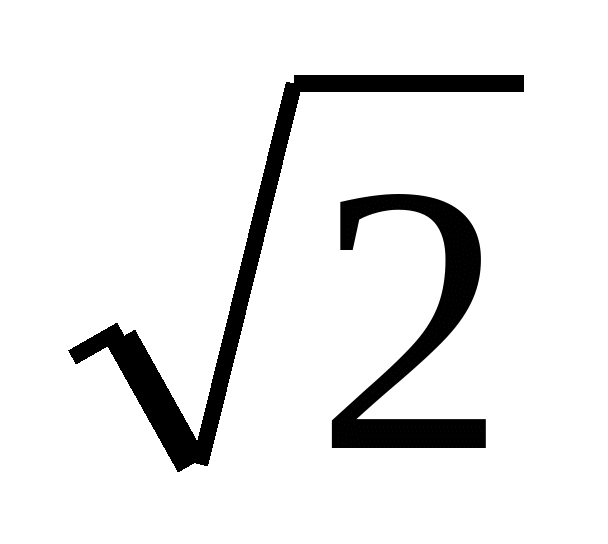 . Це число нам відоме, і воно не ціле і не дріб. Отже, ні в 5-му класі, ні в 6-му, ні в 7-му, координату точки D учні не знайшли б.
. Це число нам відоме, і воно не ціле і не дріб. Отже, ні в 5-му класі, ні в 6-му, ні в 7-му, координату точки D учні не знайшли б.
Тому до сих пір і казали “координатна пряма”, а не “числова пряма”.
Відмітимо, що був ще один недолік в знаннях з алгебри. Розглядаючи вираз із змінними, завжди вважалось, що змінні можуть набувати будь-яких значень, але тільки раціональних, бо не було інших. На справді змінні можуть набувати будь-які дійсні значення. Наприклкад, в тотожності
(a+b)(a-b)=a2-b2
в ролі a і b можуть бути будь-які дійсні числа.
Для дійсних чисел a, b, c виконуються такі закони:
а+b=b+a;
аb=ba;
а+(b+c)=(a+b)+c;
а(bc)=(ab)c;
(a+b)c=ac+bc та інші.
Правила також виконуються:
Добуток (частка) двох додатних чисел-додатне число;
Добуток (частка) двох від’ємних чисел-додатне число;
Добуток (частка) додатнього і від’ємного чисел-від’ємне число.
Дійсні числа можна порівнювати одне з одним, використовуючи наступне означення.
Означення. Кажуть, що дійсне число а більше (менше) дійсного числа b, якщо їх різниця а-b-додатнє (від’ємне число). Пишуть a>b (a<b).
З цього означення видно, що будь-яке додатнє число а більше 0 ( оскільки різнця а-0=а-додатнє число), а будь-яке від’ємне число b менше 0 (оскільки різнця b-0=b- від’ємне число). Отже,
a>0 –означає, що а-додатнє число;
a<0 –означає, що а- від’ємне число;
a-b>0 –означає, що а-b додатнє число,тобто a>b;
a-b<0 – означає, що а-b від’ємне число,тобто a<b;
Поряд із знаками строгих нерівностей (<,>) використовуються знаки нестрогих нерівностей:
а≥0 означає, що а більше або рівне нулю.
а≤0 означає, що а менше або рівне нулю.
а≥b означає, що а більше або рівне b.
а≤b означає, що а менше або рівне b.
Наприклад, для будь-якого числа а справедлива нерівність а2≥0; для будь-яких чисел а і b справедливо: (а+b)≥0.
Взагалі для порівняння дійсних чисел необов’язково кожен раз складати різницю і з’ясовувати, додатна вона чи від’ємна. Можна зробити відповідний висновок порівнюючи записи чисел у вигляді десяткових дробів.
Геометрична модель множини дійсних чисел, тобто числова пряма, робить операцію порівняння чисел особливо наочною; з двох чисел а і b більше те, яке розміщене на числовій прямій правіше.
Приклад 1. Порівняйте числа:
а) 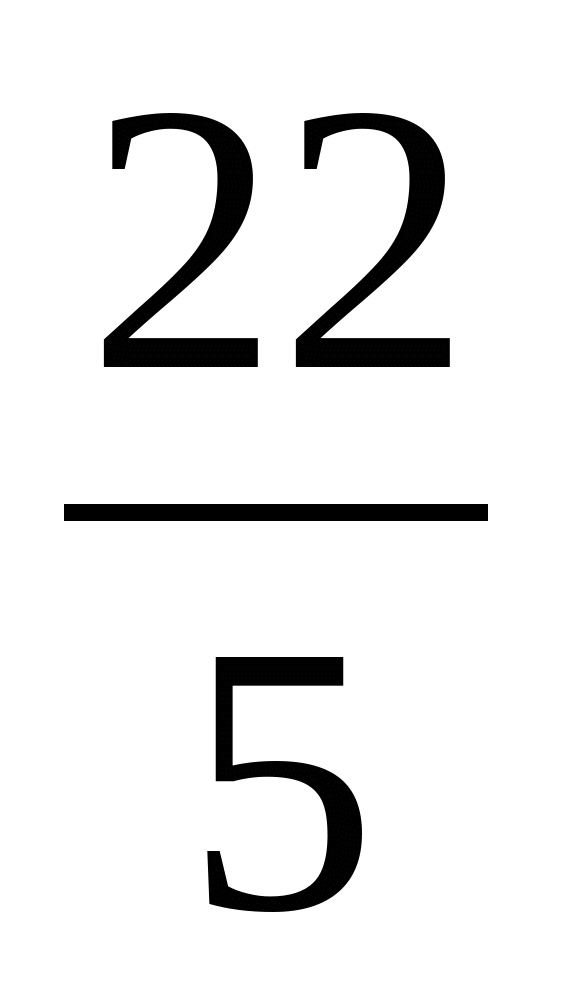 і 4; б) 2+
і 4; б) 2+ і 5; в) –3,7 і
і 5; в) –3,7 і 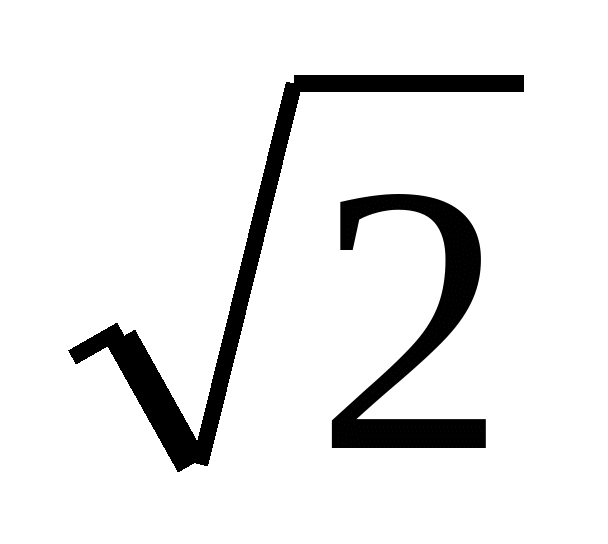 ; г) -
; г) - і -
і -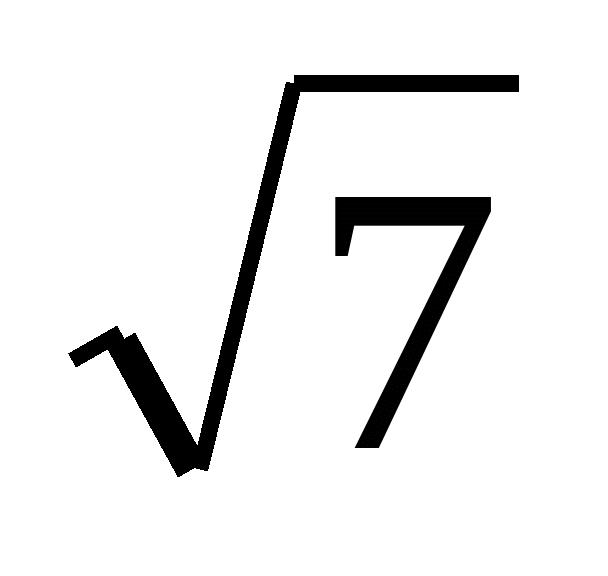 .
.
Розв'язування.
а) Маємо 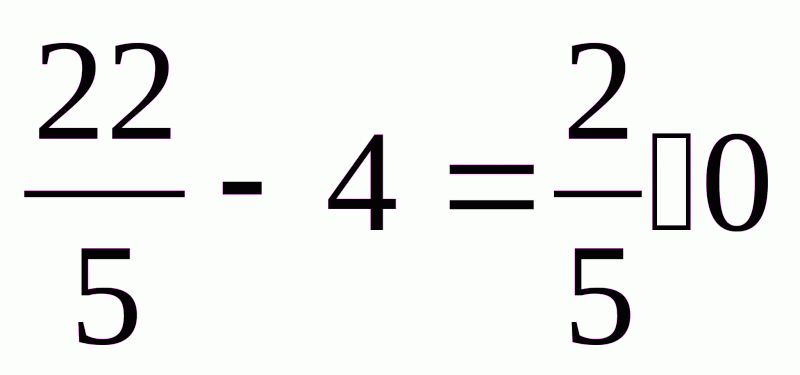 ; отже
; отже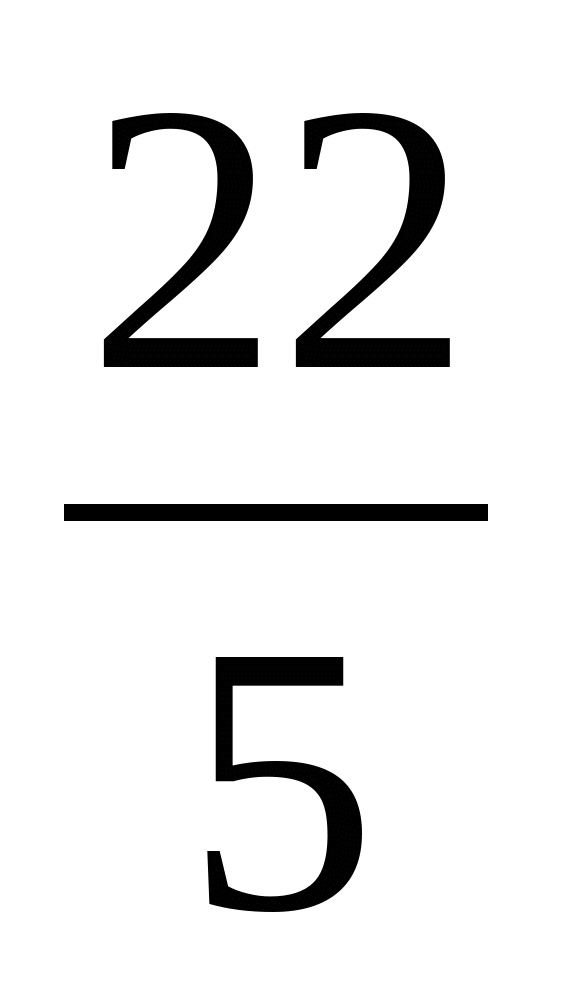 >4.
>4.
б) Маємо 2+ = 2+2,236…=4,236…<5; тому 2+
= 2+2,236…=4,236…<5; тому 2+ <5.
<5.
в) –3,7—від’ємне число, 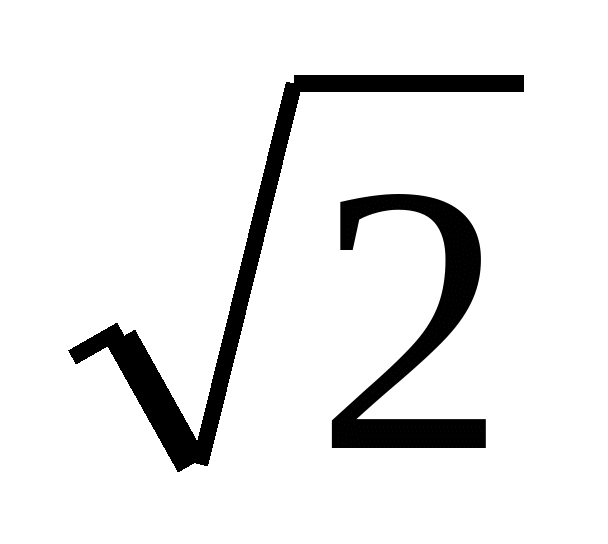 - додатнє. Будь-яке додатнє число більше за будь-яке від’ємне, тому –3,7<
- додатнє. Будь-яке додатнє число більше за будь-яке від’ємне, тому –3,7<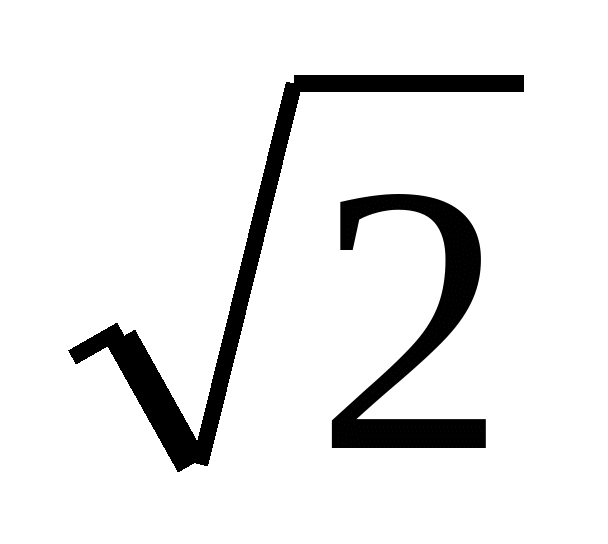 ;
;
г) -
 -2,23; -
-2,23; -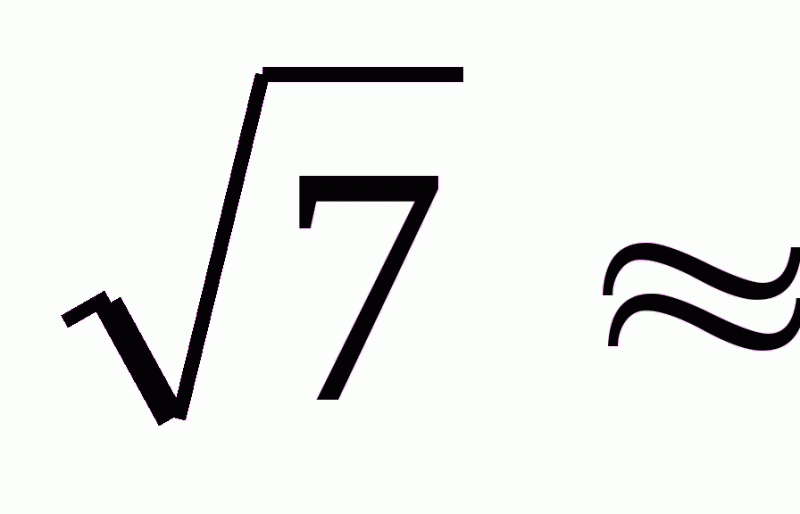 -2,64. Точка –2,64 розміщена на числовій прямій лівіше точки –2,36, тому -
-2,64. Точка –2,64 розміщена на числовій прямій лівіше точки –2,36, тому - >-
>-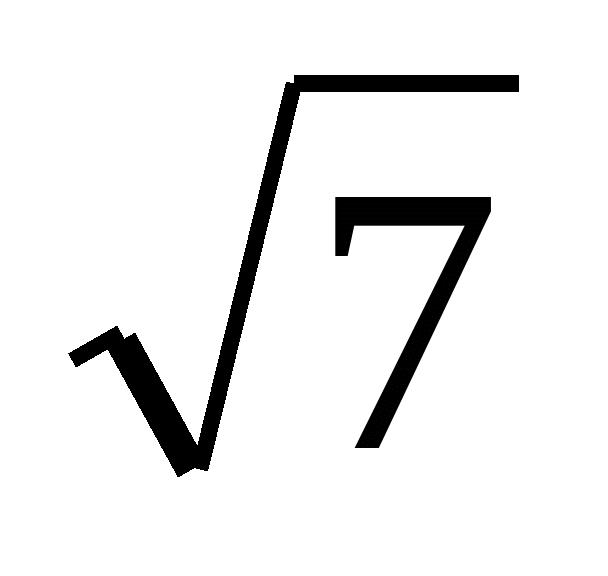 .
.
Приклад 2. Розмістити в порядку зростання числа:
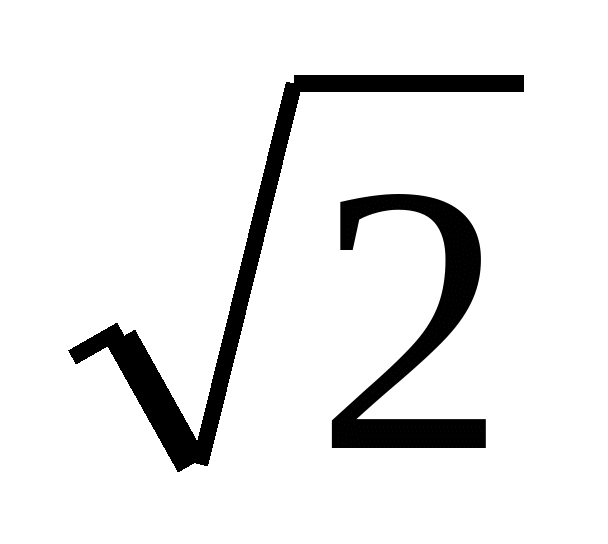 , -
, -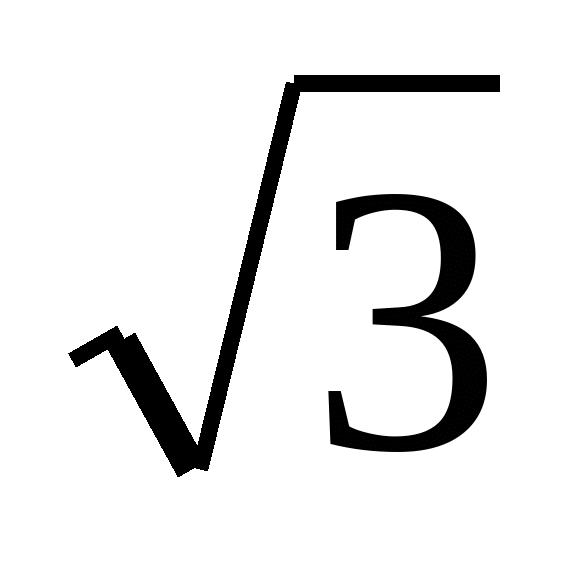 , -2,
, -2,  ,
,  ,
,  .
.
Розв'язування.
Скористаємось тим, що 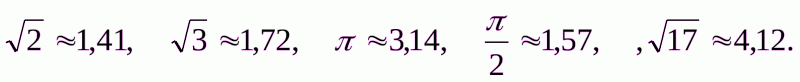 . Тоді дані числа будуть розміщені таким чином:
. Тоді дані числа будуть розміщені таким чином: 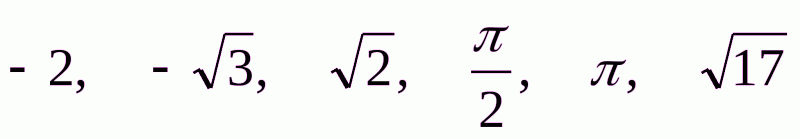 .
.
§4.Модуль дійсного числа.
4.1. Модуль дійсного числа і його властивості.
В молодших класах учні вже зустрічались з поняттям модуля (або абсолютної величини) числа, користувалися позначенням │а│. Вони знають, що, наприклад │5│=5, │-3│=3. Правда, раніше мова йшла лише про раціональні числа. Тепер потрібно ввести поняття модуля для будь-якого дійсного числа.
Означення.Модулем невід’ємного дійсного числа називають саме це число: │х│=х; модулем від’ємного дійсного числа х називають протилежне число: │х│=-х.
Скорочено це записують так:
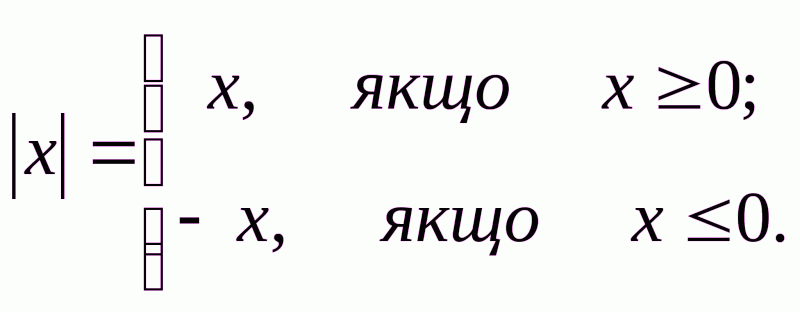 (1).
(1).
Наприклад: │5│=5; │-5│=-(-5)=5; │-3,7│=-(-3,7)=3,7; │ -2│=
-2│= -2 (бо
-2 (бо  -2>0); │
-2>0); │ -3│=-(
-3│=-( -3)=3-
-3)=3- (бо
(бо  -3<0).
-3<0).
На практиці використовують різні властивості модулів, наприклад:
1. │а│≥0;
2. │ab│=│a││b│;
3.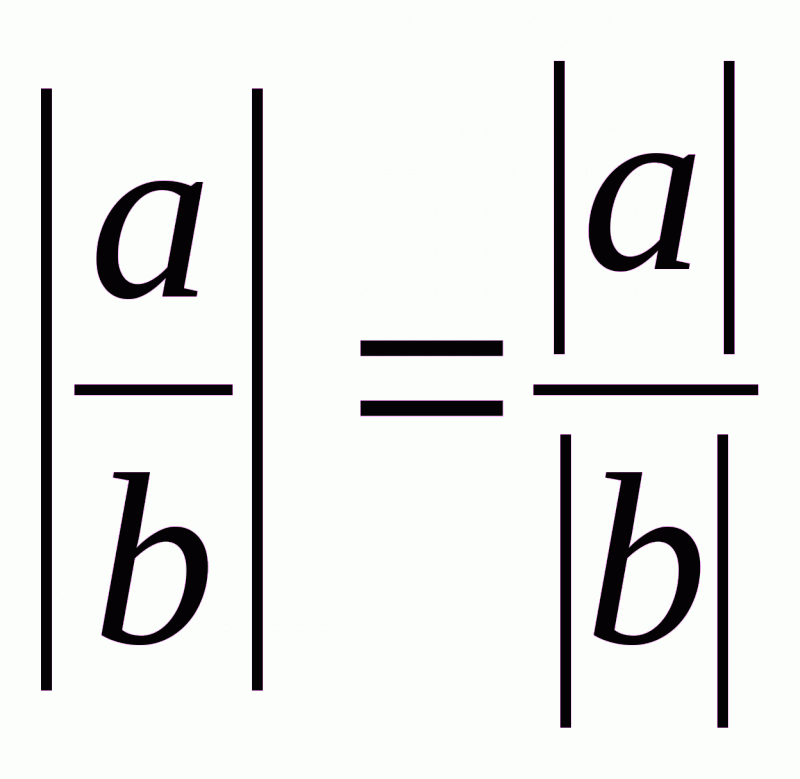 ;
;
4.│a│2=a2;
5. │a│= │-a│.
4.2. Геометричний зміст модуля дійсного числа.
Б
удемо розглядати множину R дійсних чисел і її геометричну модель –числову пряму. Позначимо на прямій дві точки а і b (а,b дійсні числа), позначимо через ρ(а,b) відстань між точками а і b. Ця відстань дорівнює b-а, якщо b>a, якщо a>b, вона дорівнює а-b, а якщо а=b то відстань рівна нулеві.
Всі три випадки виражаються формулою:
ρ(а,b)= │a-b│.
Приклад 1. розв'язати рівняння:
а) │х-2│=3; б) │х+3,2│=2; в)│х│=2,7; г)│х-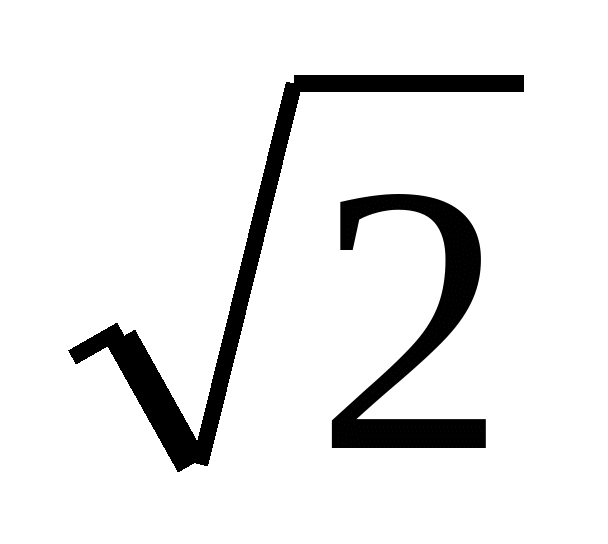 │=0;
│=0;
Розв'язування.
А) Переведемо аналітичну модель │х-2│=3 на геометричну мову: нам потрібно знайти на числовій прямій такі точки х, які задовільняють умову ρ(х,2)=3, тобто віддалені від точки 2 на відстань, яка рівна 3. Це точки –1 і 5. Звідси рівняння має два корені: -1 та 5.
Б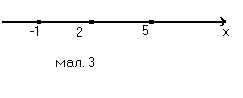
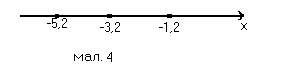 ). Рівняння │х+3,2│=2 перепишемо у вигляді │х-(-3,2)│=2 і далі ρ(х,-3,2)=2. На числовій прямій є дві точки які віддалені від точки –3,2 на відстань рівну 2. Це точки –5,2 і –1,2. Отже рівняння має два корені: -5,2 і –1,2.
). Рівняння │х+3,2│=2 перепишемо у вигляді │х-(-3,2)│=2 і далі ρ(х,-3,2)=2. На числовій прямій є дві точки які віддалені від точки –3,2 на відстань рівну 2. Це точки –5,2 і –1,2. Отже рівняння має два корені: -5,2 і –1,2.
В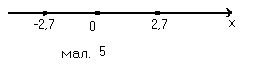 ). Рівняння │х│=2,7 перепишемо у вигляді │х-0│=2,7, або ρ(х,0)=2,7. На числовій прямій є дві точки віддалені від точки 0 на відстань 2,7. Це точки –2,7 і 2,7. Таким чином рівняння має 2 корені: -2,7 і 2,7.
). Рівняння │х│=2,7 перепишемо у вигляді │х-0│=2,7, або ρ(х,0)=2,7. На числовій прямій є дві точки віддалені від точки 0 на відстань 2,7. Це точки –2,7 і 2,7. Таким чином рівняння має 2 корені: -2,7 і 2,7.
Г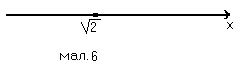 ). Для рівняння │х-
). Для рівняння │х-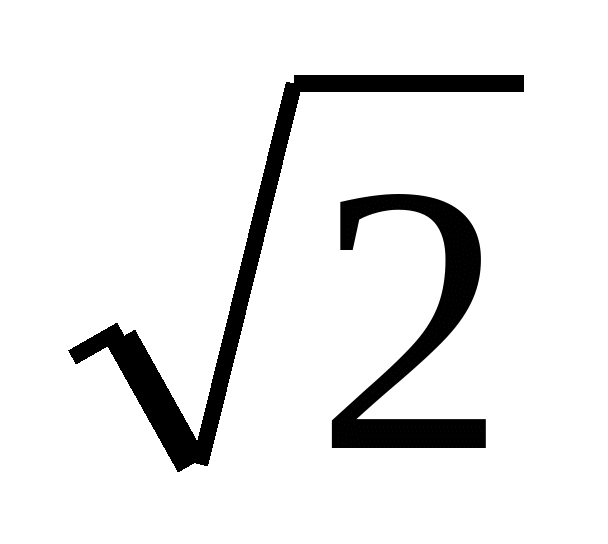 │=0 можна не використовувати геометричну ілюстрацію, бо якщо │а│=0, то а=0. Тому х-
│=0 можна не використовувати геометричну ілюстрацію, бо якщо │а│=0, то а=0. Тому х-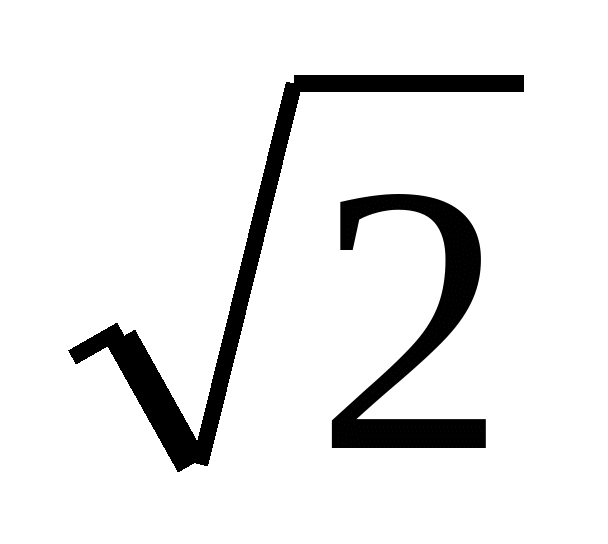 =0, тобто х=
=0, тобто х=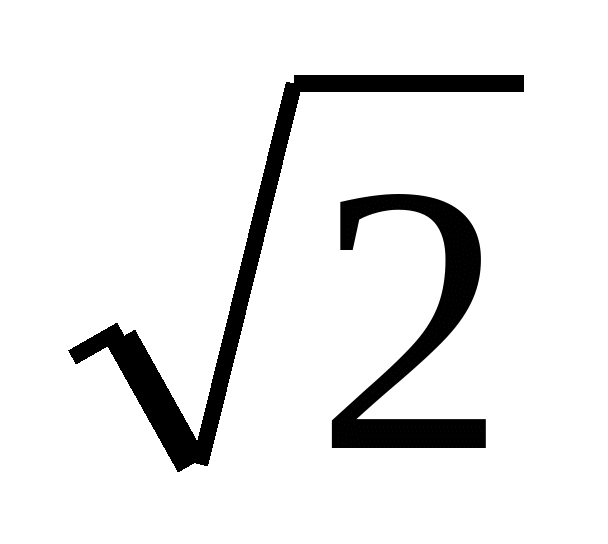 .
.
Приклад 2. Розв'язати рівняння:
а) │2х-6│=8; б) │5-3х│=6; в) │4х+1│=-2.
Розв'язування.
а) Маємо │2х-6│=│2(х-3)│=│2││х-3│=2│х-3│=8, отже дане рівняння можна спростити │х-3│=4.
П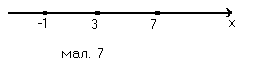 ереведемо його на геометричну модель: нам потрібно знайти такі точки х на числовій прямій, які задовільняють умову ρ(х,3)=4, тобто віддалені від точки 3 на відстань рівну 4. Це точки –1 і 7. Отже рівняння має два корені –1 і 7.
ереведемо його на геометричну модель: нам потрібно знайти такі точки х на числовій прямій, які задовільняють умову ρ(х,3)=4, тобто віддалені від точки 3 на відстань рівну 4. Це точки –1 і 7. Отже рівняння має два корені –1 і 7.
б ) Маємо│5-3х│=│(-3)(х-
) Маємо│5-3х│=│(-3)(х-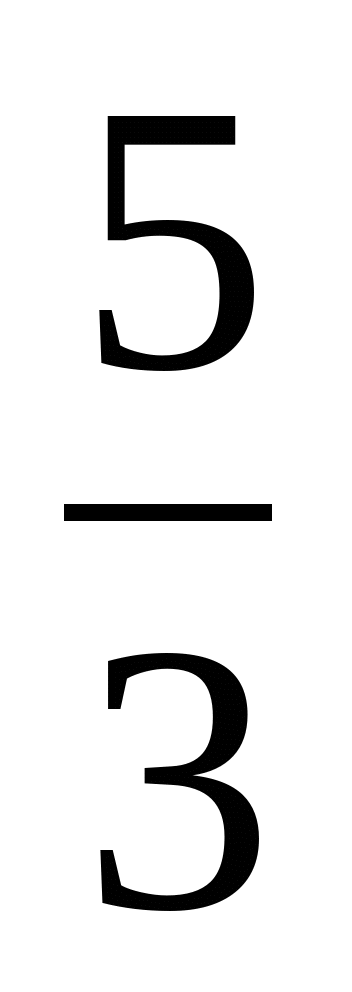 )│=│-3││х-
)│=│-3││х-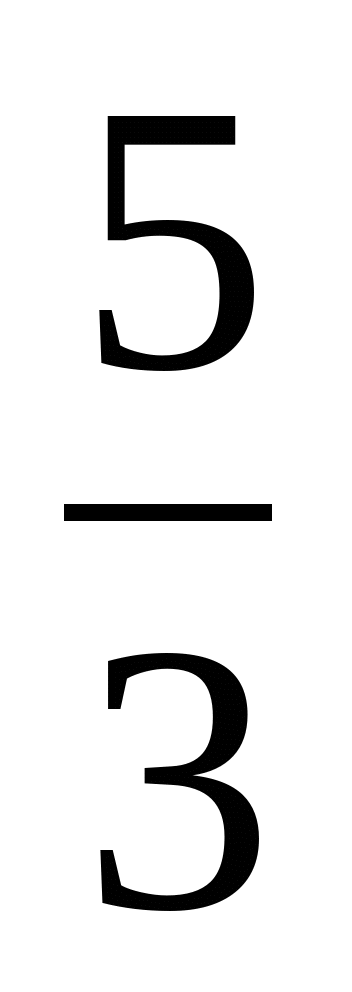 │=3│х-
│=3│х-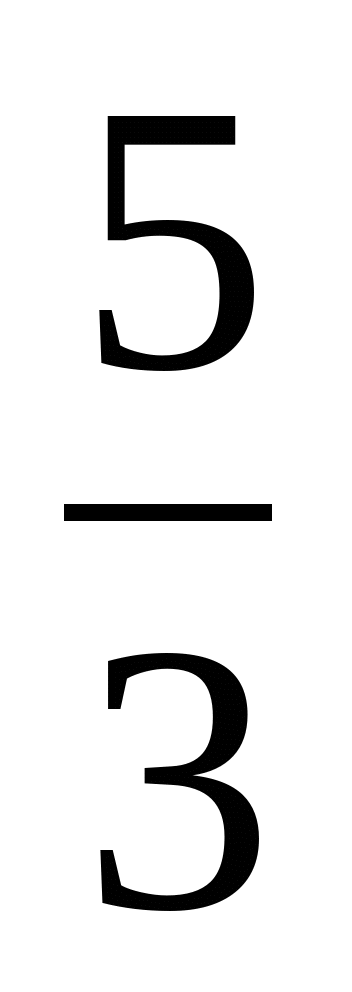 │. Це рівняння можна перетворити 3│х-
│. Це рівняння можна перетворити 3│х-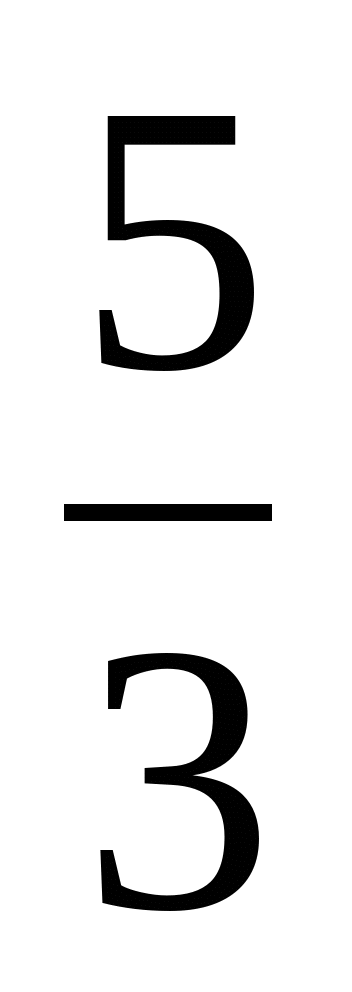 │=6 звідки │х-
│=6 звідки │х-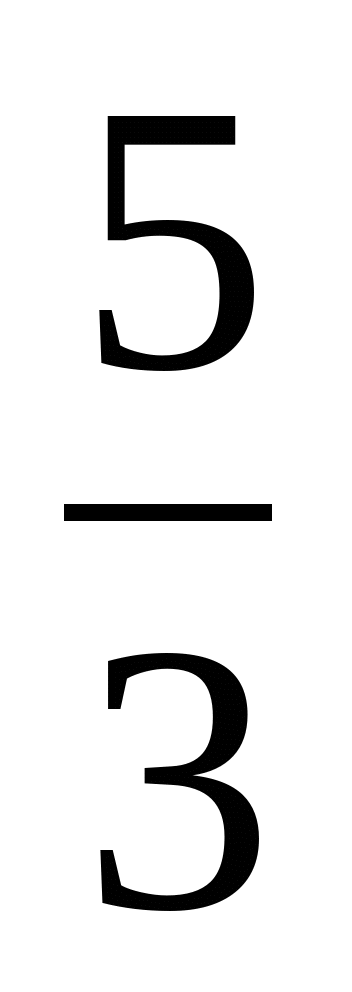 │=2, аналогічно попереднього рівняння маємо ρ(х,
│=2, аналогічно попереднього рівняння маємо ρ(х, 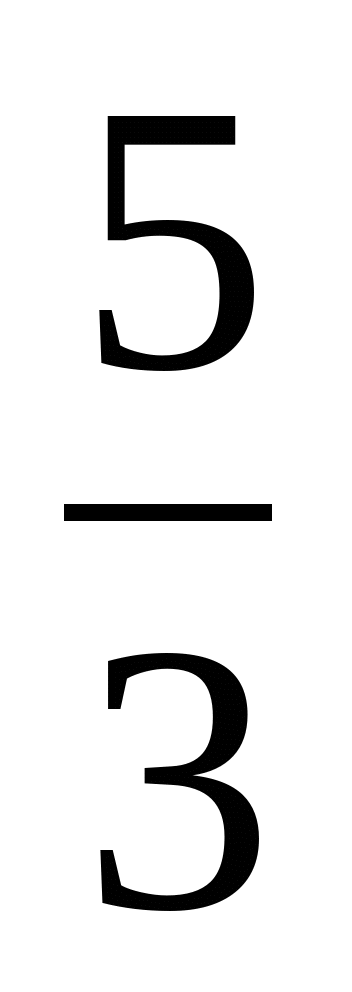 )=2. В результаті одержимо точки -
)=2. В результаті одержимо точки -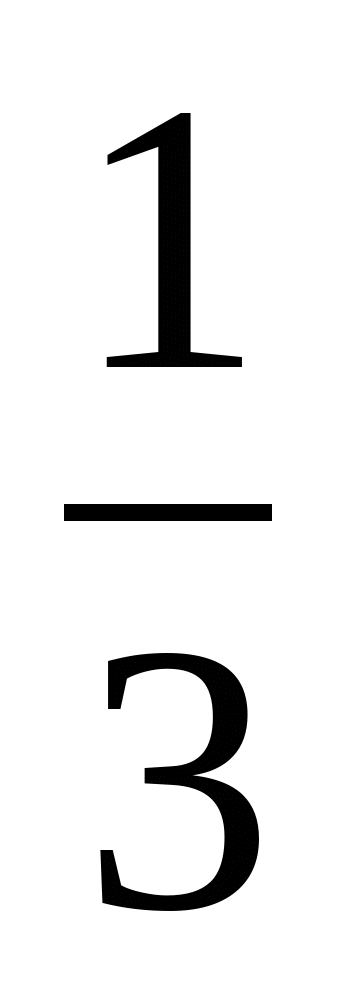 і
і 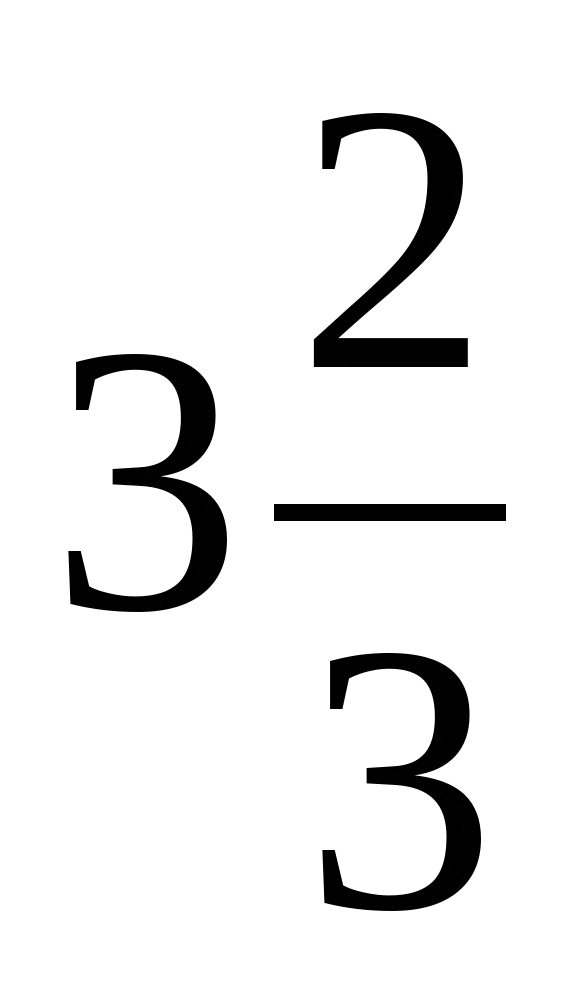 , тому рівняння має два розв'язки -
, тому рівняння має два розв'язки -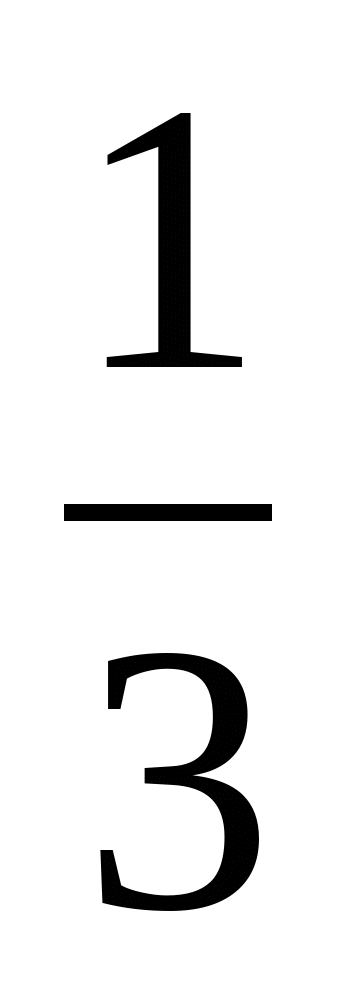 і
і 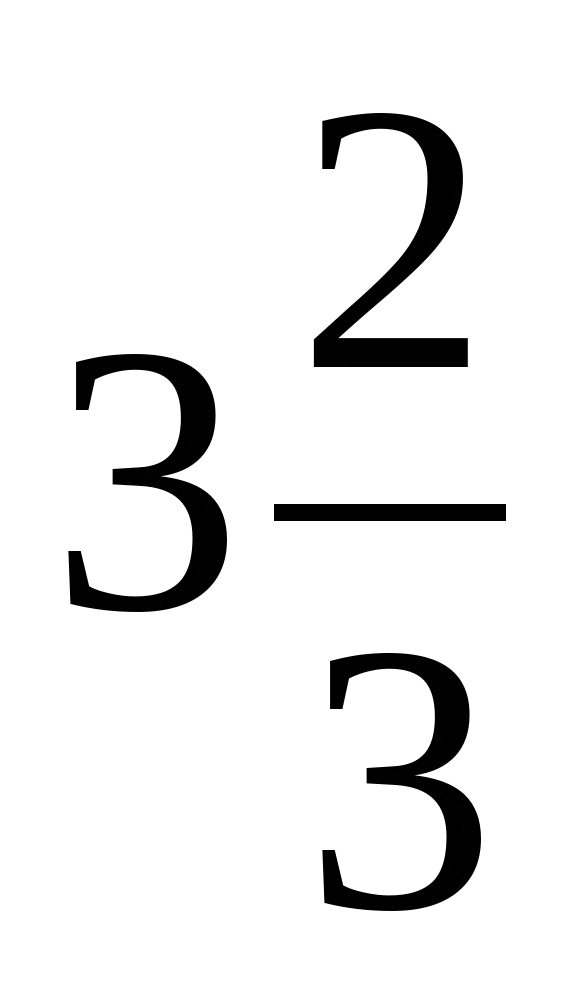 .
.
В) Для рівняння│4х+1│=-2 ніяких перетворень робити не треба. Воно не має коренів, тому, що у лівій його частині є невід’ємний вираз, а в правій від’ємне число.
4.3. Функція y=│х│.
Д
ля будь-якого дійсного числа х можна обчислити │х│, тобто можна говорити про функцію y=│х│. Скористувавшись співвідношенням (1) можна записати:

Побудову графіка будемо здійснювати “частинами”. Спочатку будуємо пряму у=х і виділимо її частину на промені [0,+∞) (мал.1). потім будуємо пряму у=-х і виділимо частину на (-∞,0) (мал.2). тепер обидві частини зобразимо в одній системі координат –це і є графік функції y=│х│ (мал.3).
Приклад 3. Побудувати графік функції у= │х+2│.
Розв'язування.
Графік цієї функції отримується з графіка функції y=│х│ зміщенням останнього на дві одиниці масштабу вліво (мал.4).
4.4. Тотожність  =│а│.
=│а│.
Ми знаємо, що якщо а≥0, то 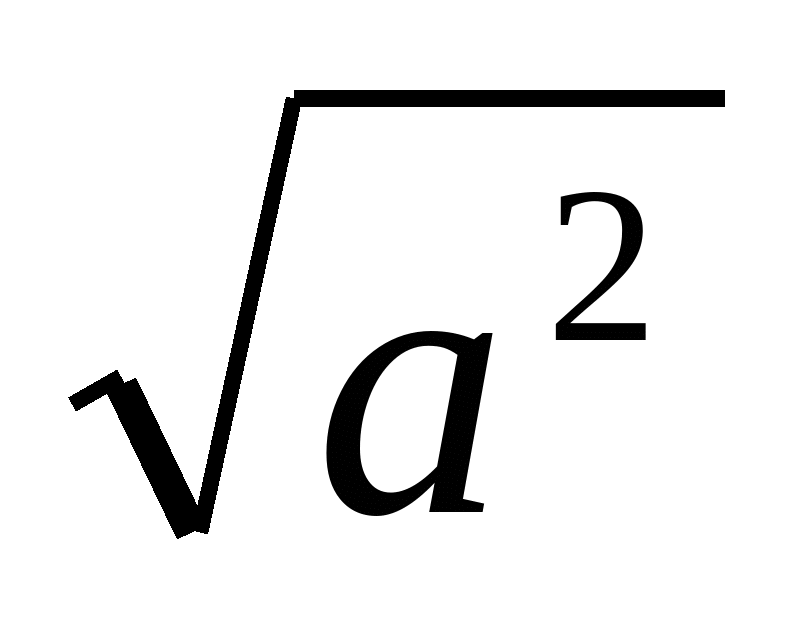 =а. А якщо а≤0? Написати
=а. А якщо а≤0? Написати 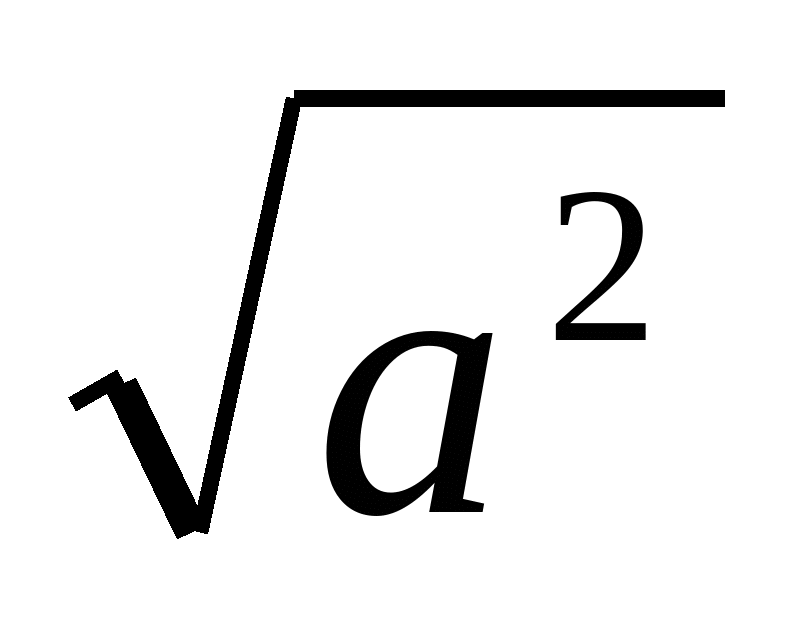 =а не можна, бо а<0 і буде
=а не можна, бо а<0 і буде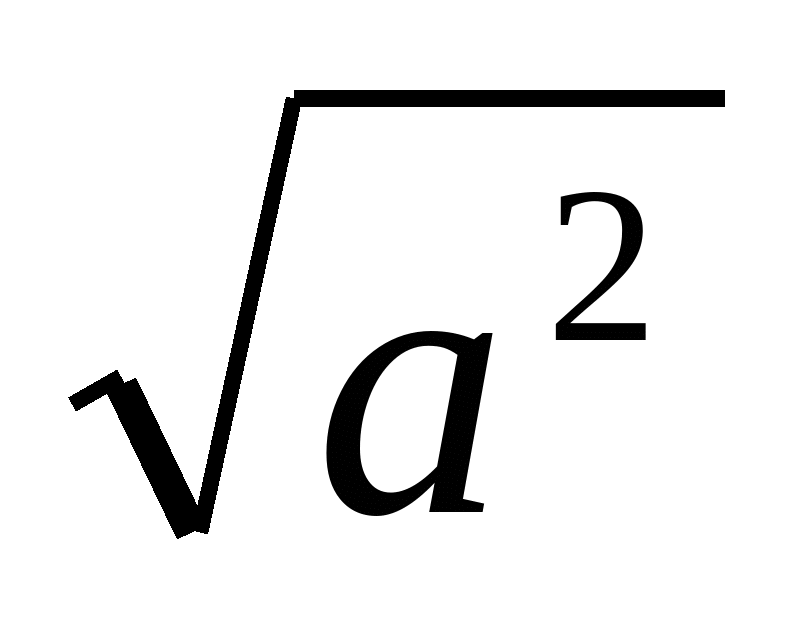 <0, а це неправильно бо значення квадратного кореня невід’ємне. З’ясуємо чому рівний вираз
<0, а це неправильно бо значення квадратного кореня невід’ємне. З’ясуємо чому рівний вираз 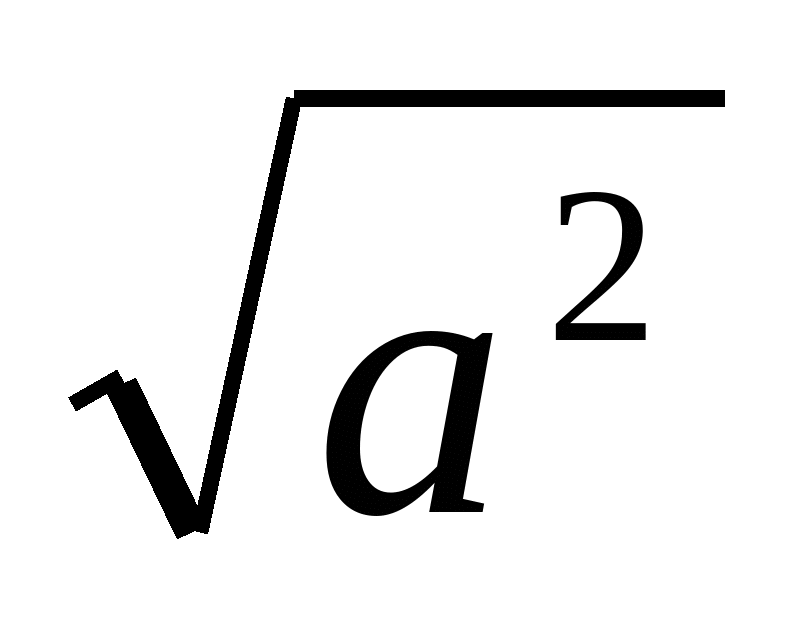 при а<0.
при а<0.
За означенням квадратного кореня у результаті повинно вийти таке число, яке по-перше додатнє, і по-друге при піднесенні до квадрату повинно дорівнювати підкореневому виразу, тобто а2. Таким числом буде а, якщо: 1) а>0, 2) (-а)2=а2. Отже,
а, якщо х≥0;
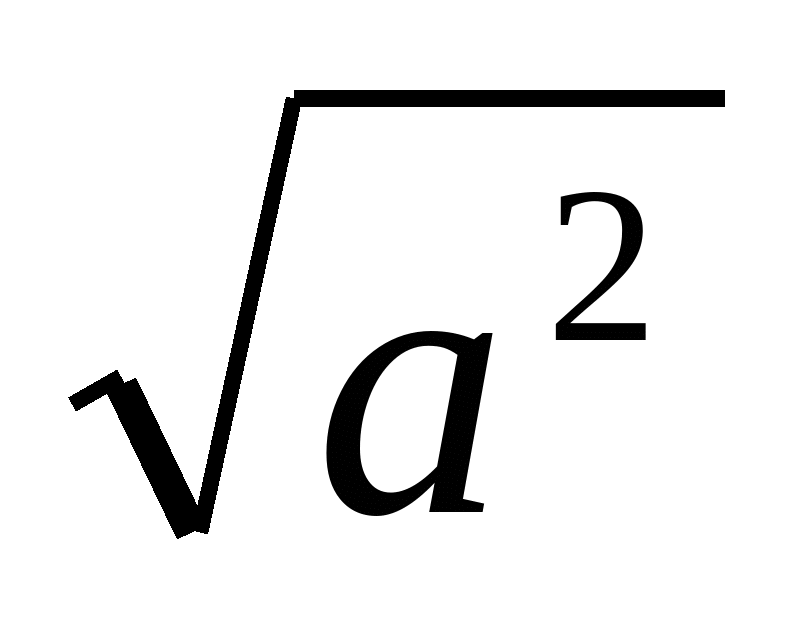
 =
=
-а, якщо а≤0.
Структура отримана в правій частині співпадає із співвідношенням (1). Отже, 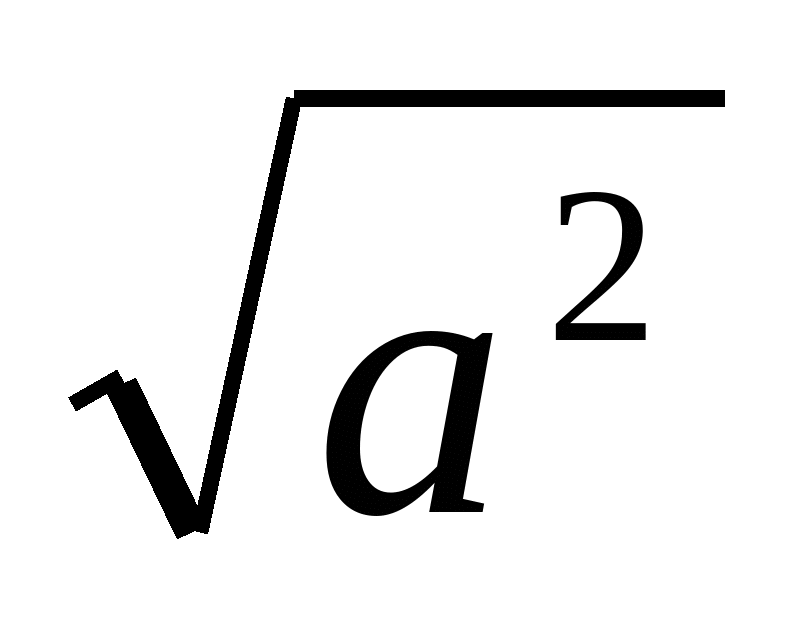 і │а│--одне і теж. Цим ми довели важливу тотожність:
і │а│--одне і теж. Цим ми довели важливу тотожність: 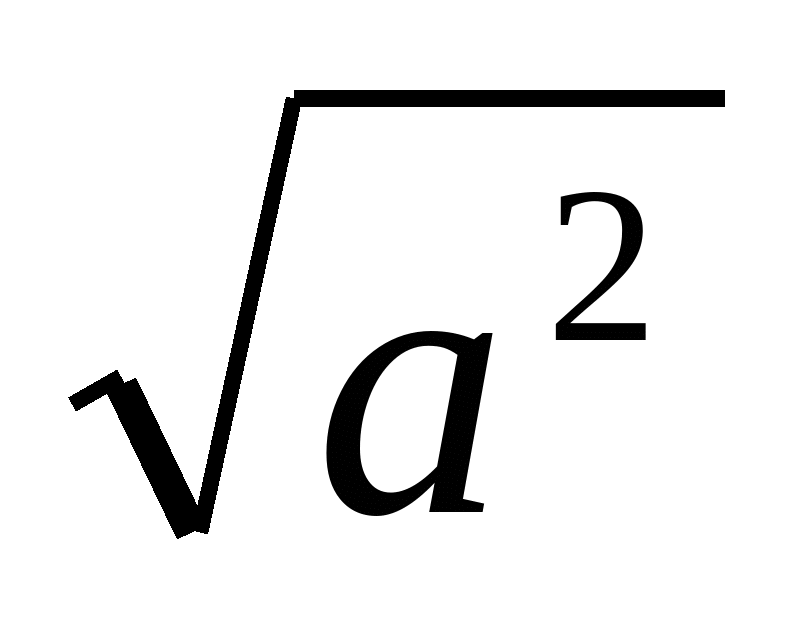 = │а│. В ролі аможе бути будь-який числовий або алгебраїчний вираз.
= │а│. В ролі аможе бути будь-який числовий або алгебраїчний вираз.
Приклад 4. Спростіть вираз 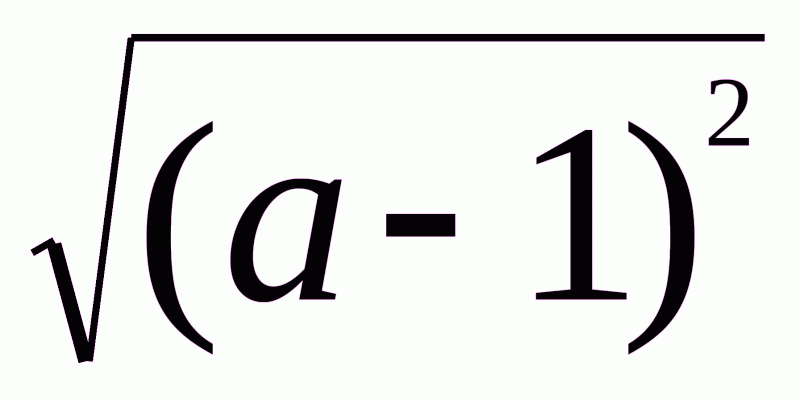 , якщо: а) а-1>0; б)а-2<0.
, якщо: а) а-1>0; б)а-2<0.
Розв'язування.
Оскільки 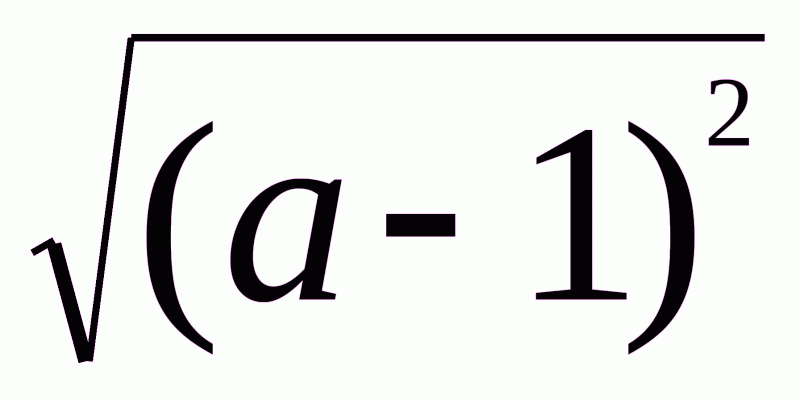 =│а-1│, то
=│а-1│, то
А) якщо а-1>0, 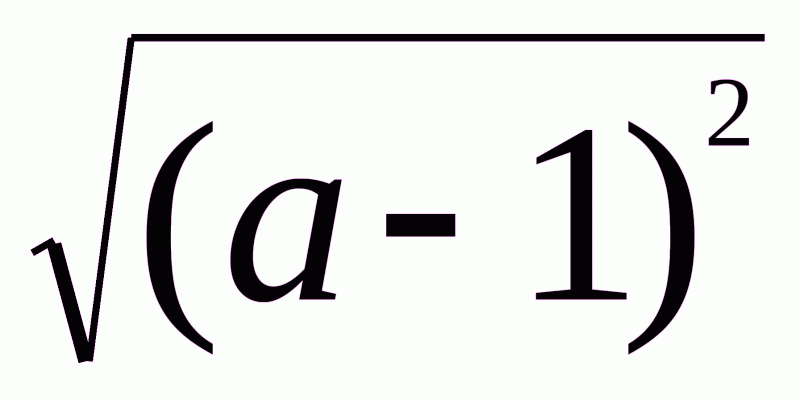 =а-1;
=а-1;
Б) якщо а-1<0, 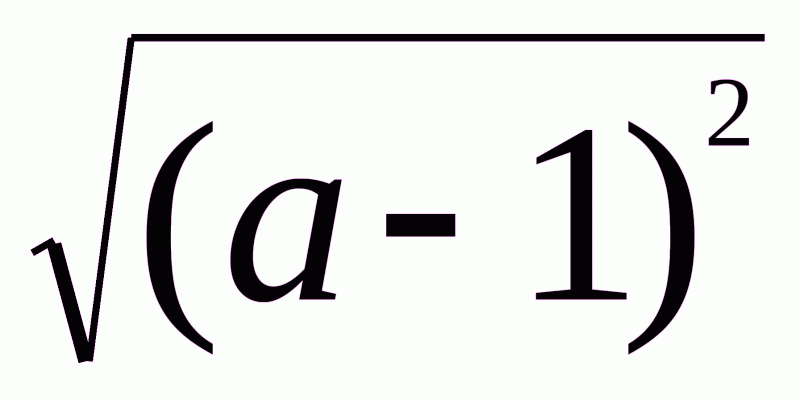 =-(а-1)=1-а.
=-(а-1)=1-а.
Приклад 5. Спростіть вираз 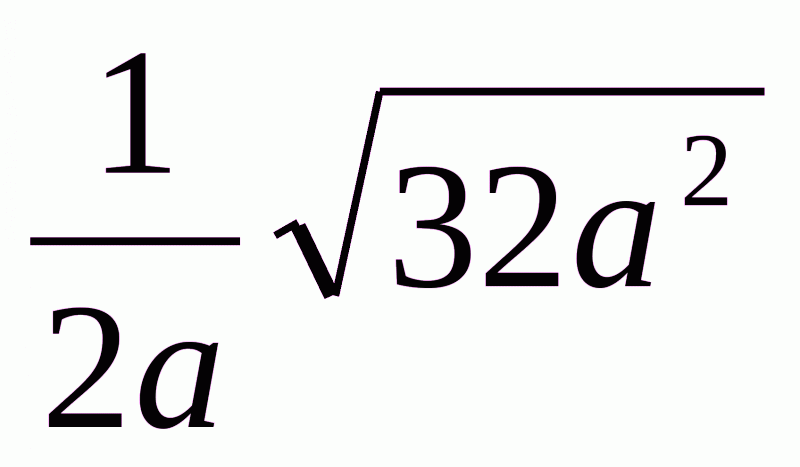 , якщо а<0.
, якщо а<0.
Розв'язування.
Маємо 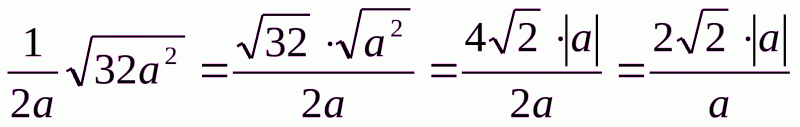 , оскільки за умовою а<0, то │а│=-а. Врезультаті маємо:
, оскільки за умовою а<0, то │а│=-а. Врезультаті маємо:
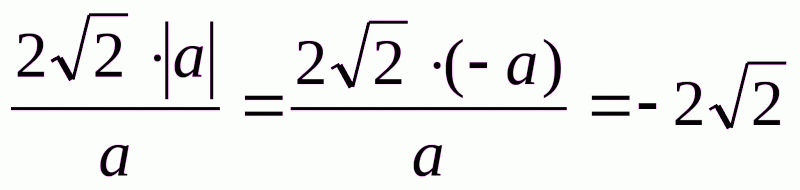 .
.
§5. Наближені значення дійсних чисел.
В 7-му і 8-му класах учні часто розв'язували задачі графічним методом. Але в цих рівняння х були корені, які в системі координат зоображались без труднощів. Але так буває не завжди.
Р
озглянемо два рівняння 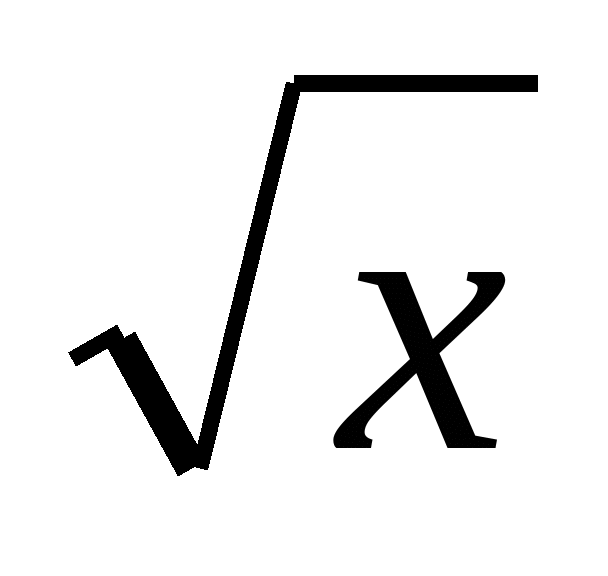 =2-х і
=2-х і 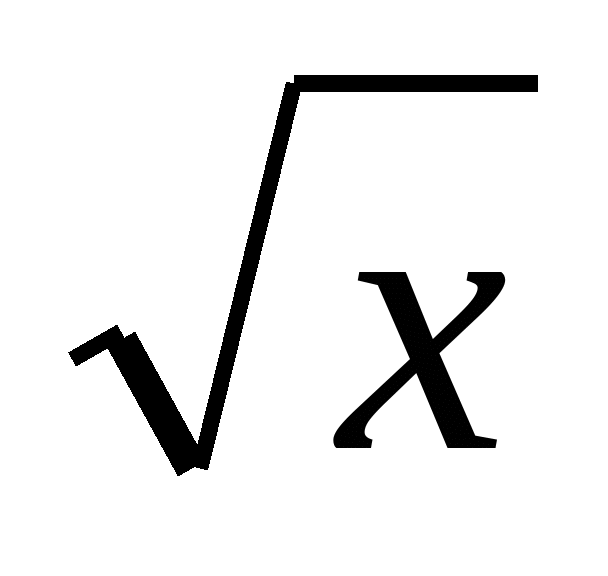 =4-х. Перше рівняння має єдиний корінь х=1, тому, що графіки функцій у=
=4-х. Перше рівняння має єдиний корінь х=1, тому, що графіки функцій у=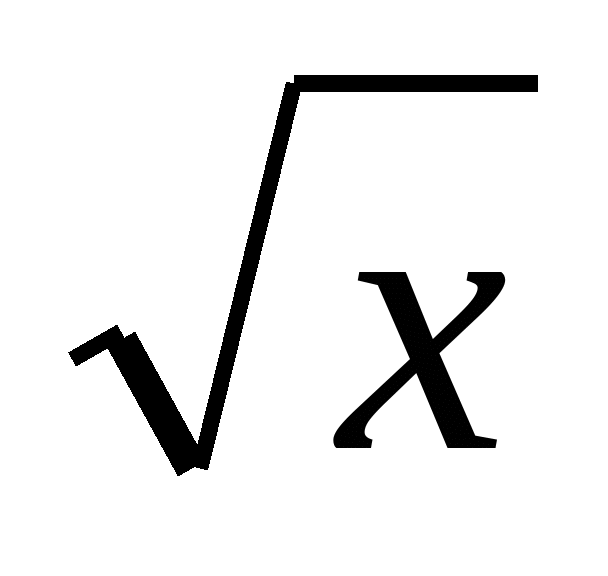 і у=2-х перетинаються в одній точці А(1,1) (мал.1). В другому випадку графіки функцій також перетинаються в одній точці В (мал.2), але з “поганими” координатами.
і у=2-х перетинаються в одній точці А(1,1) (мал.1). В другому випадку графіки функцій також перетинаються в одній точці В (мал.2), але з “поганими” координатами.
Користуючись малюнком, можна зробити висновок, що абсциса точки В приблизно рівна 2,5. В таких випадках говорять не про точний, а про приблизний розв'язок рівняння і записують так: х≈2,5.
Це одна з причин, чому математики вирішили ввести поняття наближеного значення дійсного числа. Є і інша причина, більш важлива. Що таке дійсне число? Це нескінченний десятковий дріб. Але проводити обчислення з нескінченними десятковими дробами незручно, тому на практиці користуються наближенними значеннями дійсних чисел. Наприклад для числа π=3,141592…, користуються наближенням π≈3,141 або π≈3,142. Перше називають наближеним значенням числа з недостачею з точністю до 0,001, друге—з надлишком. Можна вибрати і більш точні наближення: наприклад π≈3,1415 –наближення з недостачею з точністю 0,0001, або π≈3,1416 –наближення з надлишком з точністю 0,0001. Також можна взяти менш точні наближення, скажемо, з точністю 0,01: з недостачею π≈3,14, або з надлишком π≈3,15.
Приклад 1. Знайти наближене значення з надлишком і з недостачею з точністю до 0,01 для числа: а)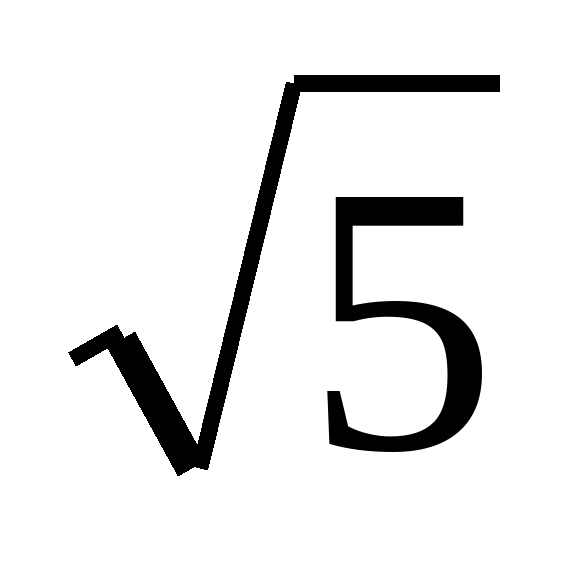 ; б)
; б) 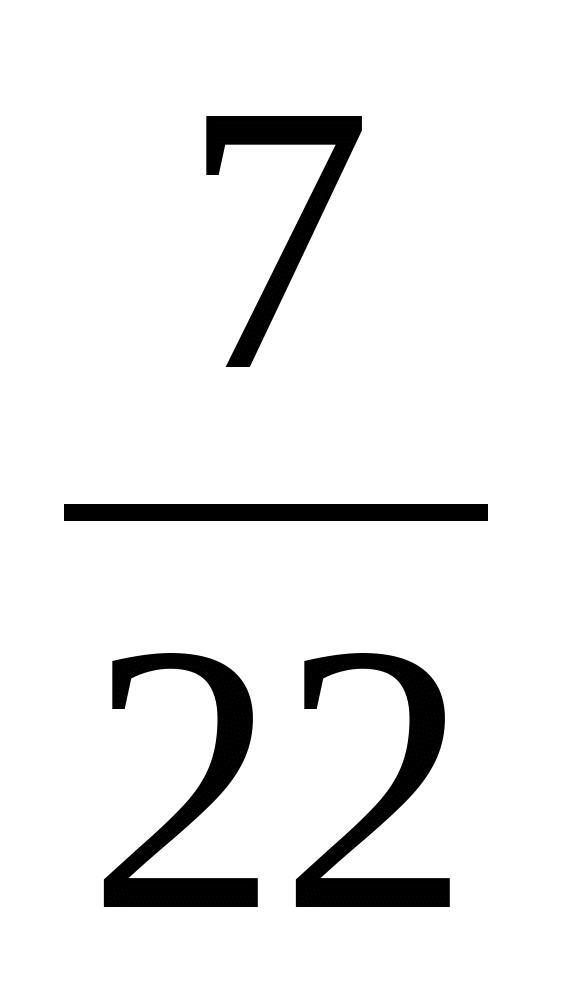 .
.
Розв'язування.
А) Ми знаємо, що 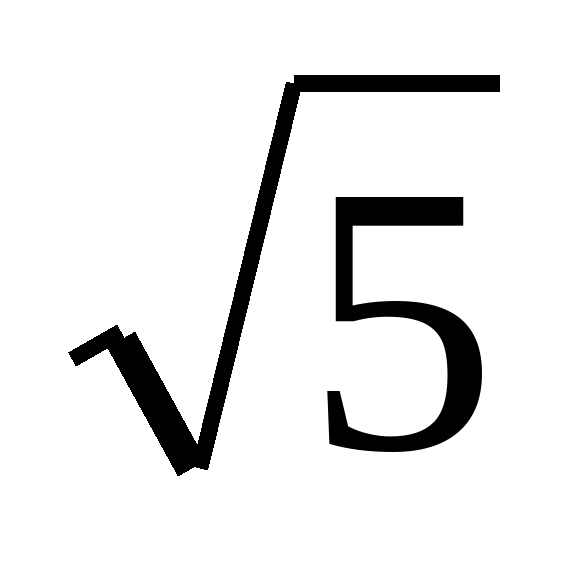 =2,236…, тому ,
=2,236…, тому , 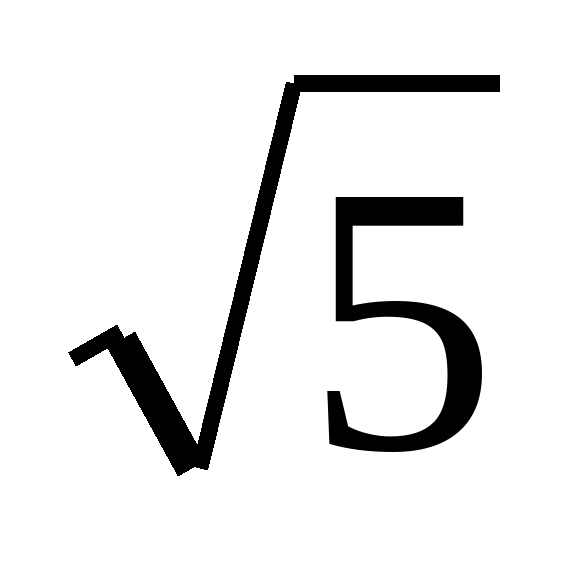 ≈2,23 з недостачею і
≈2,23 з недостачею і 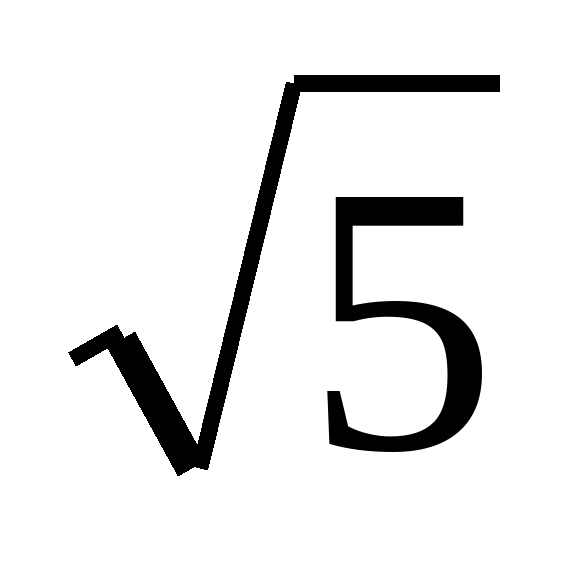 ≈2,24 знадлишком.
≈2,24 знадлишком.
Б) Маємо 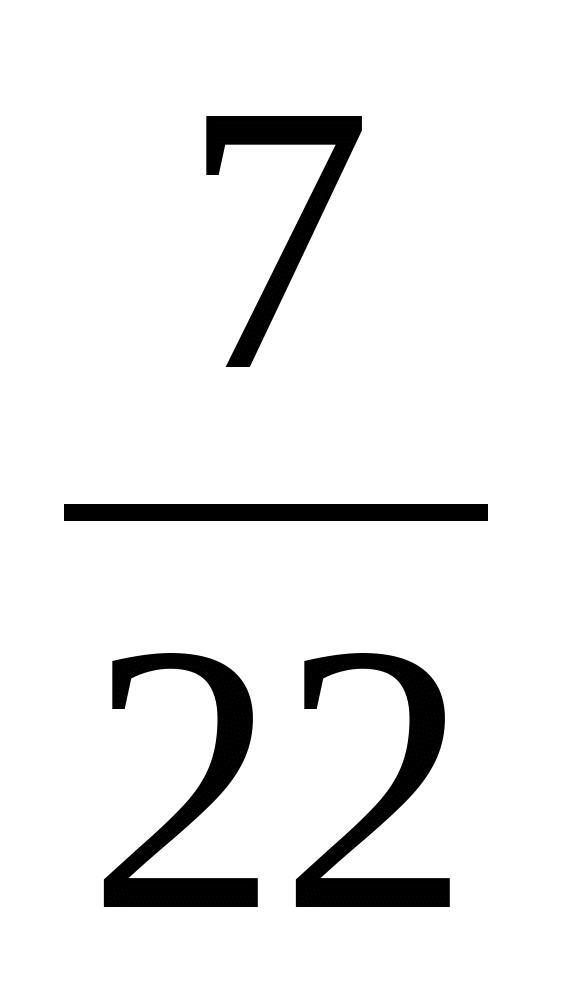 =0,3(18). Тому
=0,3(18). Тому 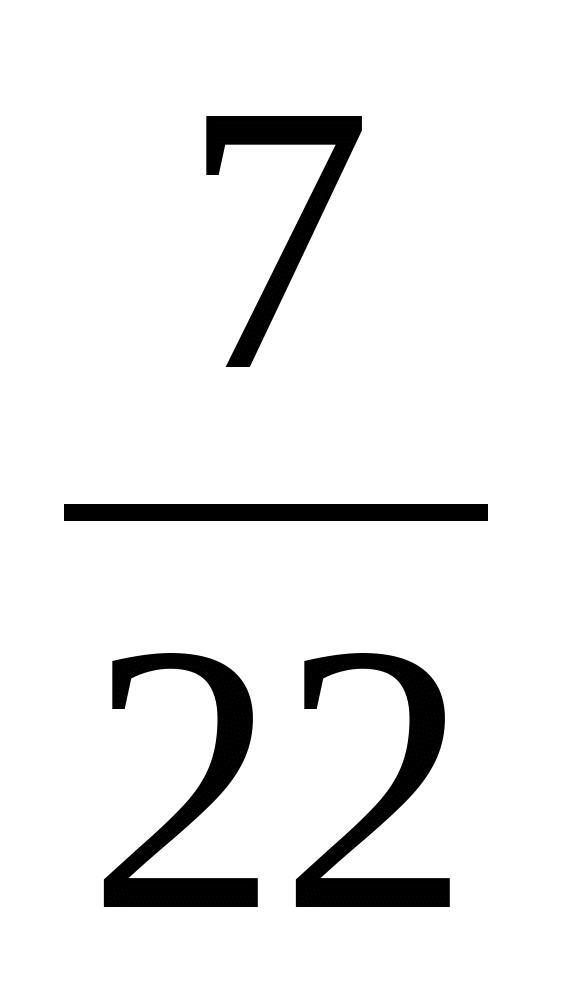 ≈0,31 з недостачею і
≈0,31 з недостачею і 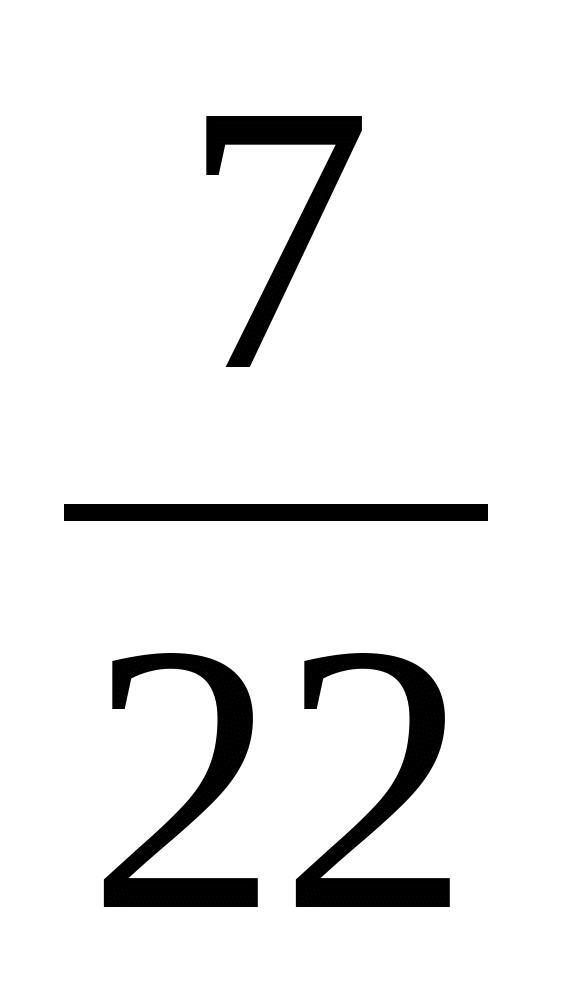 ≈0,32 з надлишком.
≈0,32 з надлишком.
Наближення з недостачею і надлишком іноді ще називають округленням числа.
Означення. Похибкою наближення (абсолютною похибкою) називають модуль різниці між точним значенням величини х і її наближенням а -│х-а│.
Виникає практичне запитання, яке наближення краще, з надлишком чи з недостачею, тобто в якому випадку похибка менша? Це, звичайно залежить від конкретного числа для якого складають наближення, тобто округлення. Як правило при округленні додатніх чисел використовують слідуюче правило.
Правило округлення.Якщо перша відкидаюча цифра менша 5, то треба брати наближення з недостачею, якщо ж перша відкидаюча цифра більша або рівна 5, то беруть наближення з надлишком.
Застосуємо це правило до деяких чисел і виберемо для них ті наближення для яких похибка буде найменша.
1)π=3,141592…, з точністю до 0,001 маємо π≈3,142, тут перша цифра, яка відкидається, 5 тому взяли наближення з надлишком. З точністю до 0,0001 маємо π≈3,1416 також наближення з надлишком. А ось з точністю до 0,01 треба взяти наближення з недостачею: π≈3,14.
2) 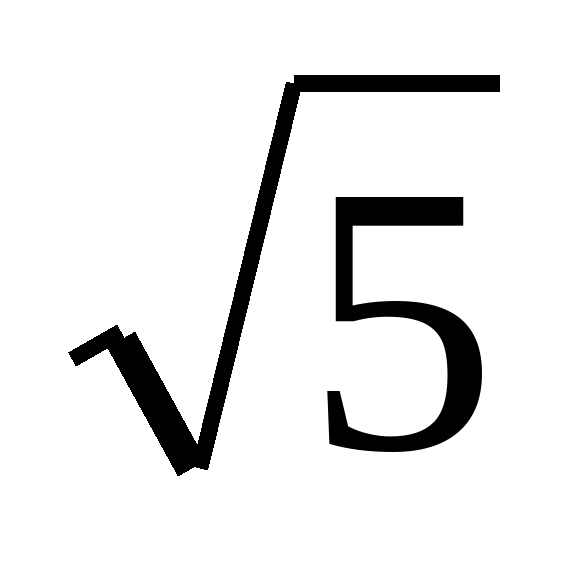 =2,236…, при наближенні з точністю до 0,01 маємо
=2,236…, при наближенні з точністю до 0,01 маємо 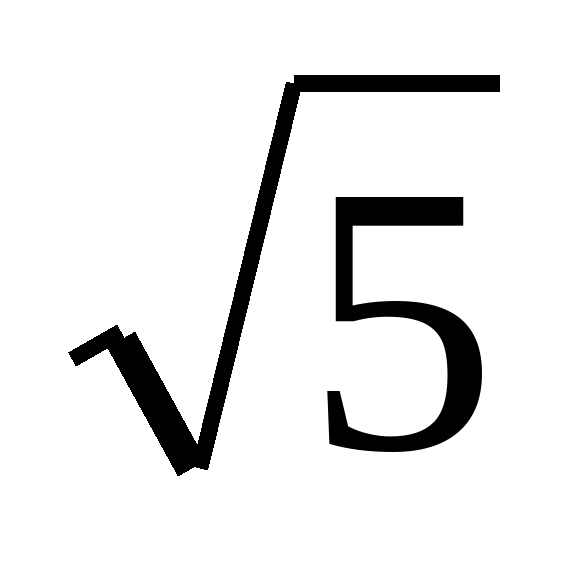 ≈2,24—наближення з надлишком.
≈2,24—наближення з надлишком.
Якщо а—наближене значення числа х і │х-а│≤h, то кажуть, щопохибка наближення не перевищує h або що число х рівне числу а з точністю до h.
РОЗДІЛ IІІ.Методика викладання даної теми в школі.
Нагадаємо, що в математиці відомо кілька теорій дійсних чисел ( Р.Дедекінда, Г.Кантора, К.Вейєрштрасса, Є.Я.Ремеза та інші ). Проте ні одна з них не зрозуміла учням. Можна з певністю сказати, що в шкільному курсі математики це одна із тем, яка б засвоювалася учнями так важко, як тема про ірраціональні числа. Тому вчитель повинен особливо добре продумувати всю систему уроків пов’язаних з цією темою.
З усіма раціональними числами –цілими і дробовими, додатними і від’ємними–учні познайомились ще в V класі, але в VIII класі, перед введенням ірраціональних чисел, бажано систематизувати їх знання. Зробити це можна, наприклад, так:
-Вам вже відомі цілі і дробові (додатні, від’ємні і нуль) числа. Всі вони, взяті разом, називаються раціональними числами. Бо кожне таке число можна подати у вигляді частки 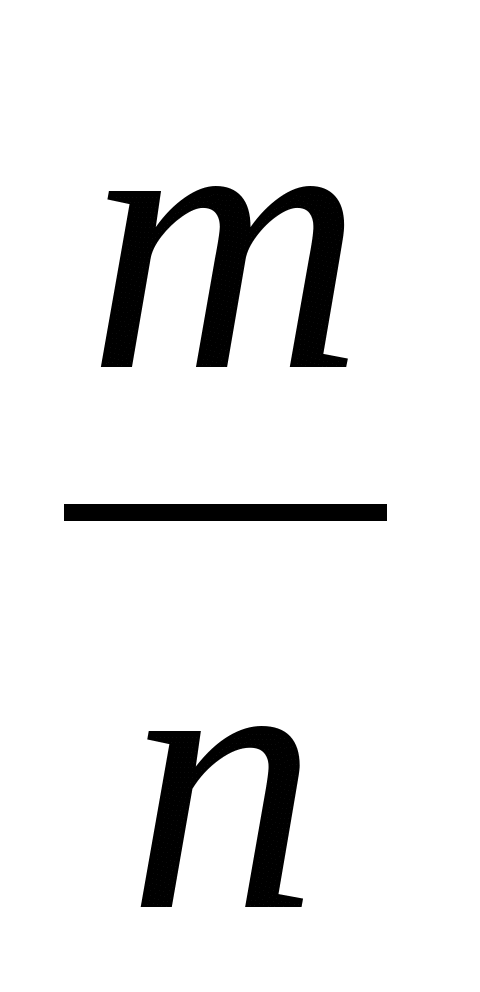 , де m– число ціле, а n– натуральне. Досі вам були відомі тільки раціональні числа, а існують і інші, нераціональні. Але перш ніж ознайомитись з ними, необхідно розглянути питання про десятковий запис раціональних чисел…
, де m– число ціле, а n– натуральне. Досі вам були відомі тільки раціональні числа, а існують і інші, нераціональні. Але перш ніж ознайомитись з ними, необхідно розглянути питання про десятковий запис раціональних чисел…
Далі на конкретних прикладах слід пояснити, що кожен звичайний дріб можна перетворити на десятковий. При цьому в одних випадках дістанемо скінченний десятковий дріб, а в інших—нескінченний, але обов’язково періодичний. Наприклад, ділячи 8 на 37 і 7 на 12, покажемо, що 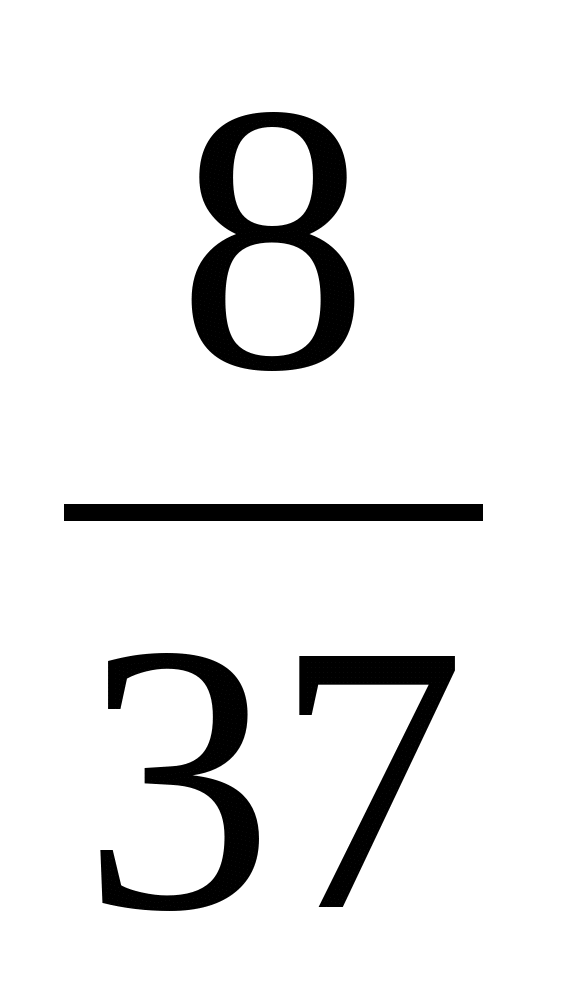 =0,216216…=0,(216),
=0,216216…=0,(216), 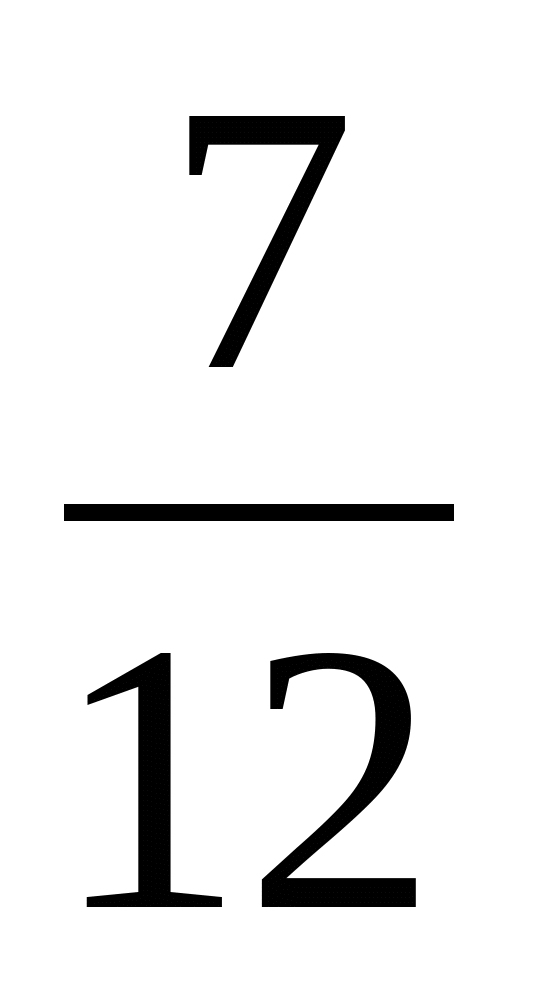 =0,5833…=0,58(3).
=0,5833…=0,58(3).
Зауваживши, що і скінченний десятковий дріб і ціле число можна зображати у вигляді нескінченного періодичного десяткового дробу з нулем в періоді: 3,6=3,6000…=3,6(0), 12=12,000…=12,(0). Формулюємо висновок. Кожне раціональне число можна подати у вигляді нескінченного періодичного десяткового дробу і кожен нескінченний періодичний десятковий дріб відповідає деякому раціональному числу.
П еред вчителем стоїть завдання – створити основу для введення ірраціональних чисел. Ця тема складна для вивчення, тому її треба викласти доступно, без багатьох означень і доведень.
еред вчителем стоїть завдання – створити основу для введення ірраціональних чисел. Ця тема складна для вивчення, тому її треба викласти доступно, без багатьох означень і доведень.
Відразу ж після ознайомлення учнів з арифметичним квадратним коренем можна пояснити учням, що не існує раціонального числа, квадрат якого дорівнює 2, і розглянути графічний спосіб розв'язування рівняння х2=2 (мал. ). Учні помічають, що пряма y=2 перетинає параболу у=х2 в двох точках з абсцисами 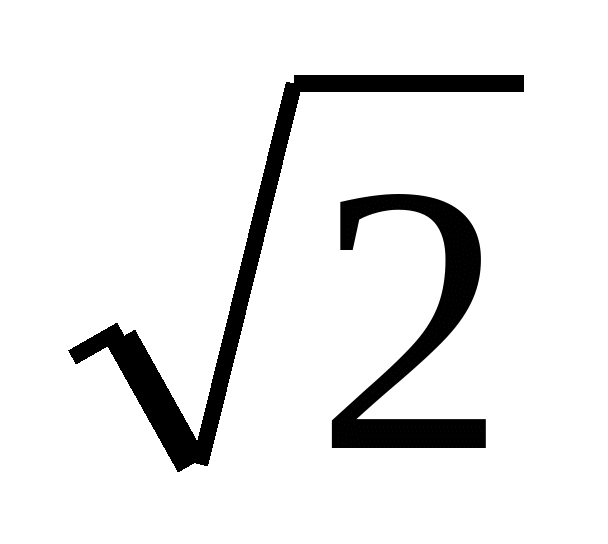 і -
і -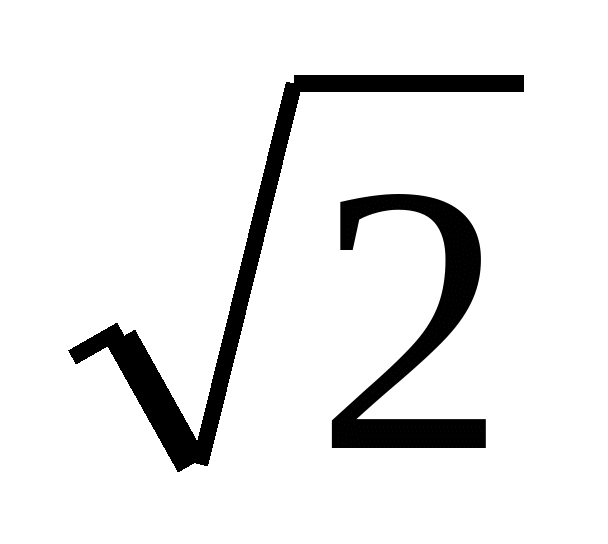 . Отже, дане рівняння має два корені. А за теоремою можна сказати що рівняння не може мати раціональних коренів. Виходить, числа
. Отже, дане рівняння має два корені. А за теоремою можна сказати що рівняння не може мати раціональних коренів. Виходить, числа 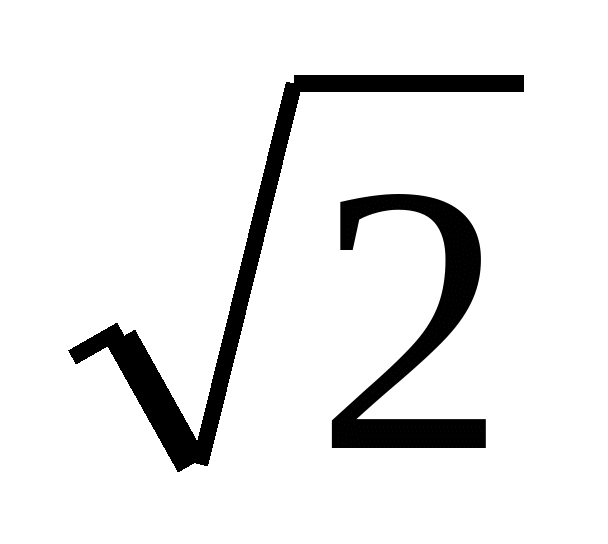 і -
і -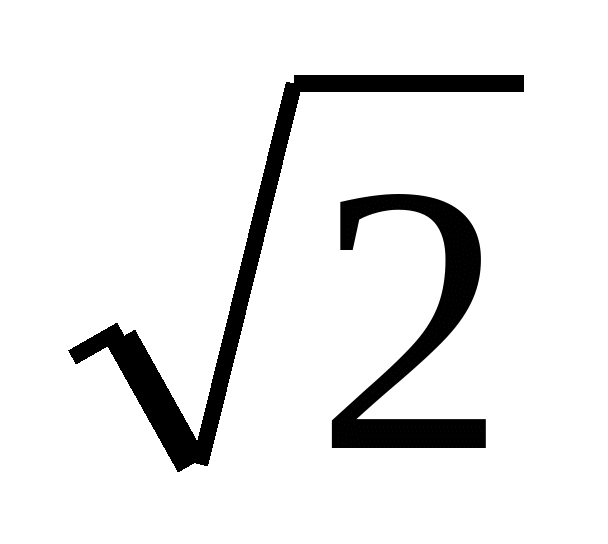 не раціональні. Так само не є раціональними числа
не раціональні. Так само не є раціональними числа 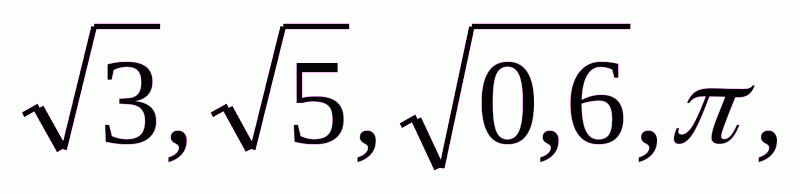 та багато інших. Їх називають ірраціональними числами. Як бачимо, основною тут є теорема про те, що не існує раціонального числа квадрат якого дорівнює 2. Її доведення розглядається ще в “Началах” Евкліда (кінець Х книги). Доведення не складне і навчальне, в сильніших класах бажано його розглянути.
та багато інших. Їх називають ірраціональними числами. Як бачимо, основною тут є теорема про те, що не існує раціонального числа квадрат якого дорівнює 2. Її доведення розглядається ще в “Началах” Евкліда (кінець Х книги). Доведення не складне і навчальне, в сильніших класах бажано його розглянути.
У методичній літературі найчастіше розглядають два способи доведення цієї теореми. Один з них грунтується на такому твердженні: “ якщо числа m і n взаємно прості, то і числа m2 і n2 взаємно прості”. Проте це твердження не відоме учням, тому його не варто використовувати в доведенні. Розглядувану теорему краще доводити так : “ так як 12=1<2, і 22=4>2 а квадрати цілих чисел більших за 2, ще більші, то не існує цілого числа, квадрат якого дорівнював би 2.
Припустимо тепер, що існує якесь дробове число, квадрат якого рівний 2. Вважатимемо, що це число виражене незворотним дробом 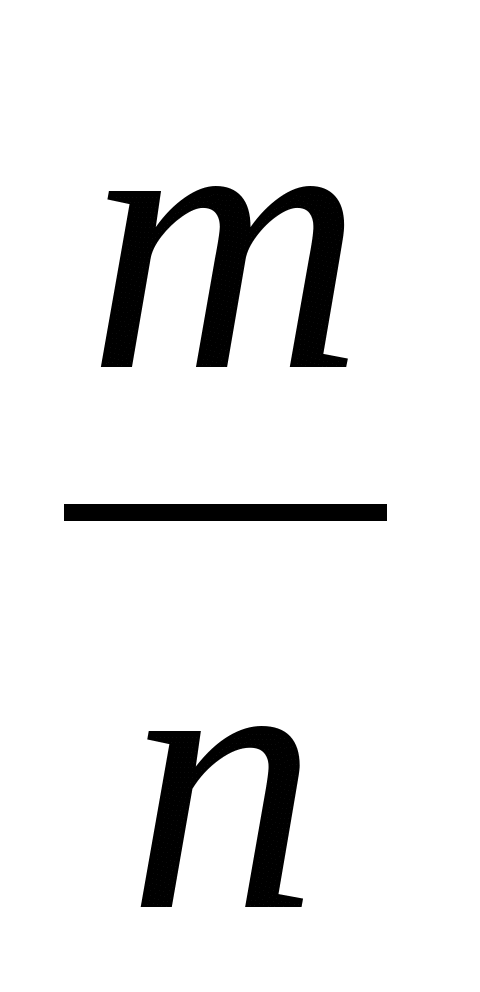 . Але якщо
. Але якщо 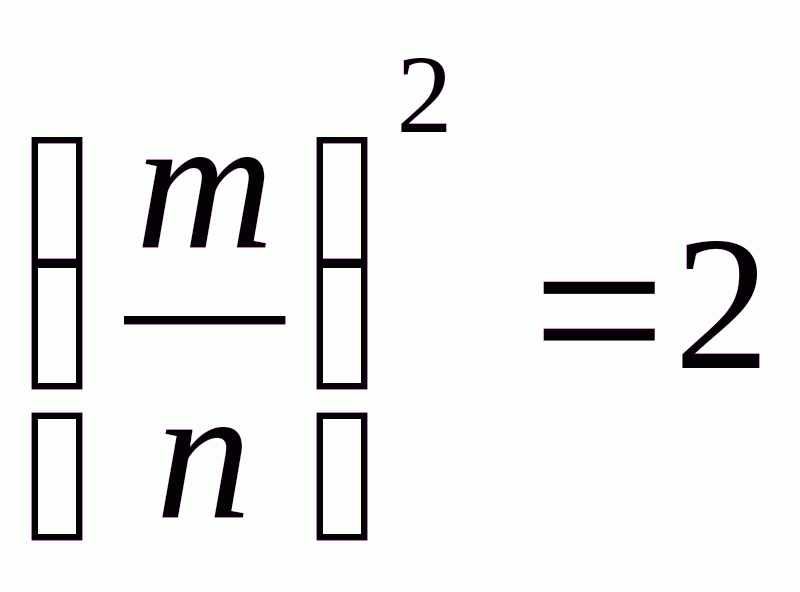 , то m2=2n2, тобто, число m2—парне. А тоді й m парне бо квадрат непарного число непарне (це випливає з тотожності (2k+1)2=4k2+4k+1). Таким чином, з припущення випливає, що m=2р, де р-якесь натуральне число. Але тоді (2р)2=2n2, звідси n2=2р2 отже число n також парне. Як бачимо, кожне з чисел m і n ділиться на 2, а це суперечить тому, що дріб
, то m2=2n2, тобто, число m2—парне. А тоді й m парне бо квадрат непарного число непарне (це випливає з тотожності (2k+1)2=4k2+4k+1). Таким чином, з припущення випливає, що m=2р, де р-якесь натуральне число. Але тоді (2р)2=2n2, звідси n2=2р2 отже число n також парне. Як бачимо, кожне з чисел m і n ділиться на 2, а це суперечить тому, що дріб 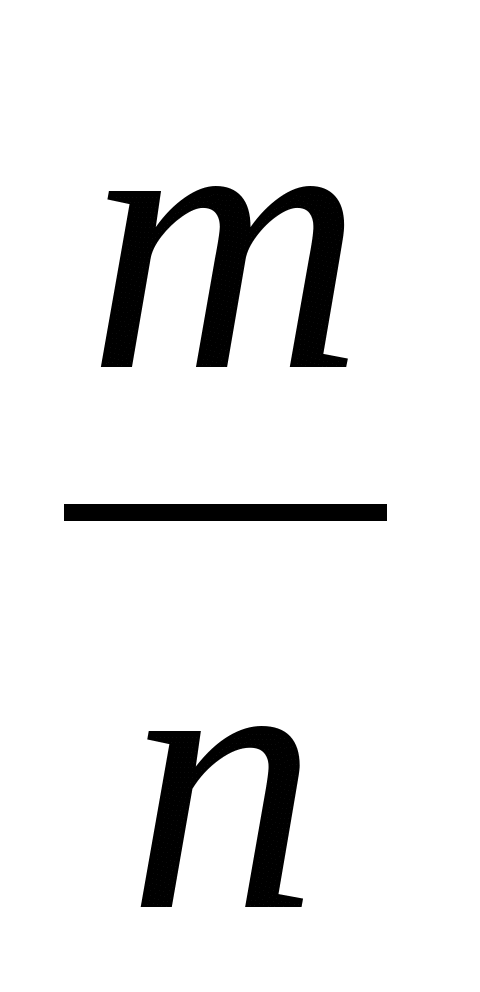 нескоротний. Виходить зроблене припущення не правильне.
нескоротний. Виходить зроблене припущення не правильне.
Отже, ні цілого, ні дробового раціонального числа, квадрат якого дорівнював би 2, не існує. Теорему доведено.
Після доведення цієї теореми бажано запропонувати учням (як задачу) довести, що не існує раціонального числа, квадрат якого дорівнював би, наприклад 5.
Зауважимо, що в деяких посібниках замість розглянутої теореми доводиться більш загальна. “Якщо натуральне число не є квадратом цілого числа, то воно не може бути і квадратом дробу”. З цієї теореми безпосередньо випливає справедливість розглянутих вище тверджень.
Після таких пояснень можна показати учням, навіщо потрібні ірраціональні числа. Це питання корисно пов’язати з вимірюванням величин, найкраще довжин відрізків. Нехай треба виміряти діагональ х квадрата, сторона якого дорівнює одиниці довжини. За теоремою Піфагора маємо: х2=2.
Але вище було доведено, що не існує раціонального числа, квадрат якого рівний 2. Як бачимо довжину діагоналі такого квадрата не можна точно виразити ніяким раціональним числом. Залишається одне з двох: або вважати, що не кожен відрізок має довжину (а це незручно в багатьох відношеннях), або розширити поняття множини раціональних чисел. Краще йти другим шляхом. Подібно до того, як раніше множину натуральних чисел доповнювали дробовими, тепер доповнимо множину раціональних чисел ірраціональними.
-Звернімося до числової осі. Як відомо, кожному раціональному числу на числовій осі відповідає одна точка. А чи кожній точці відповідає раціональне число? Відкладемо від початкової точки О числової осі відрізок ОD (мал.1. Розділ ІІ, §3), що дорівнює діагоналі одиничного квадрата. Оскільки довжину цієї діагоналі не можна точно виразити раціональним числом, то точці А не відповідає ніяке раціональне число. І таких точок існує на числовій прямій безліч. Для того щоб кожному відрізкові можна було б поставить у відповідність якесь число –його довжину необхідно розширити множину раціональних чисел –ірраціональними.
Довжина діагоналі квадрата з одиничною стороною буде дорівнювати 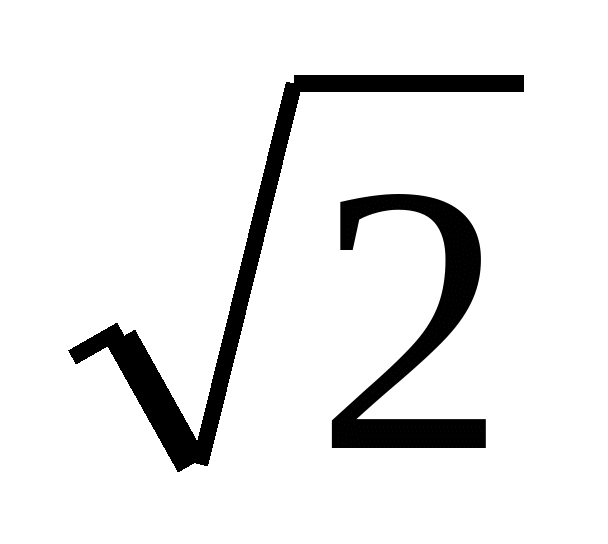 ≈1,4142135…, тобто деякому нескінченному неперіодичному десятковому дробу.
≈1,4142135…, тобто деякому нескінченному неперіодичному десятковому дробу.
Раніше ми розглядали тільки раціональні числа. Тепер будемо оперувати ірраціональнимим --деякими нескінченноми неперіодичноми десятковоми дробами.
Приклади ірраціональних чисел:
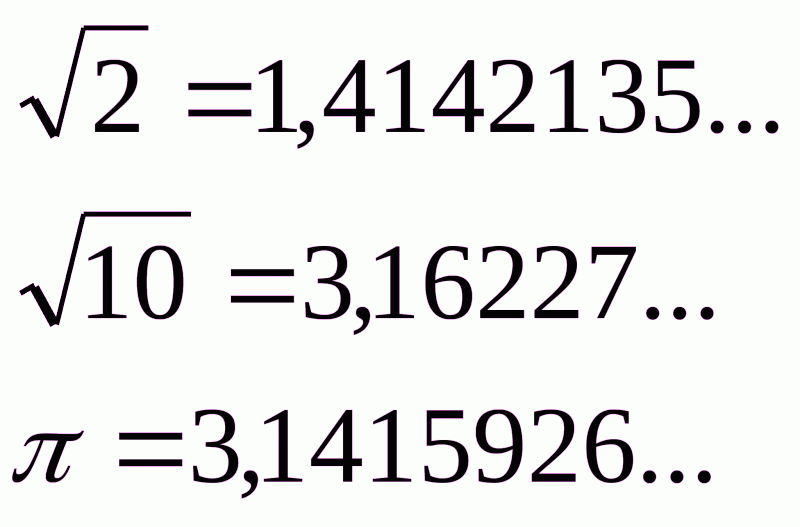
Все це додатні ірраціональні числа, але вони бувають і від’ємними, наприклад:
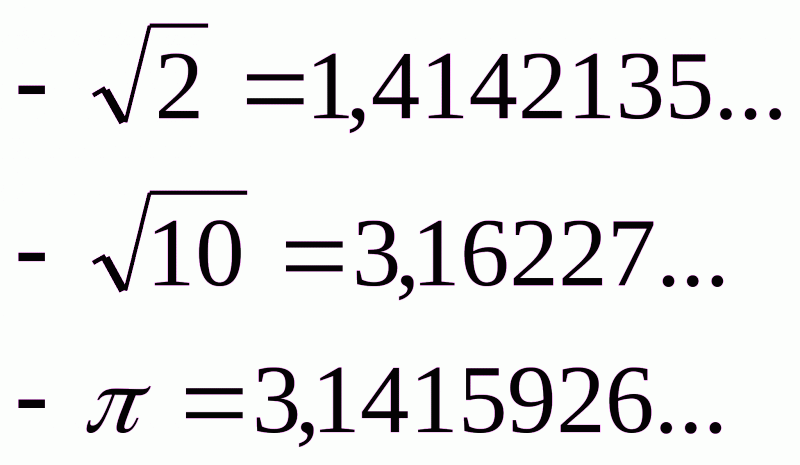
Раціональні і ірраціональні числа разом називаються дійсними.
Вводити дійсні числа можна за відомою учням схемою. Натуральні числа, нуль і протилежні натуральним числа, становлять множину цілих чисел. Числа цілі і дробові становлять множину раціональних чисел. Аналогічно: раціональні і ірраціональні числа становлять множину дійсних чисел. Сказане вище бажано ілюструвати конкретними прикладами і за допомогою схеми.
Тепер уже можна пояснити, що в множині дійсних чисел кожен відрізок має свою довжину. Довжина може виражатися раціональним або ірраціональним числом. Іноді пояснюють, що “ ірраціональні числа виражають довжини несумірних відрізків”, причому коли вживаємо термін “несумірний”, то обов’язково повинні зазначити, з чим саме цей відрізок несумірний. Тому цю думку можна сформулювати інакше :”Додатні ірраціональні числа виражають довжини відрізків, несумірних з одиничним в
Дійсні числа

ідрізком”.
Д



![]()


алі вводять поняття модуля дійсного числа і переходять до порівняння дійсних чисел.
Два дійсних числа можна вважати рівними, якщо вони мають однакові модулі і однакові знаки. Наприклад, 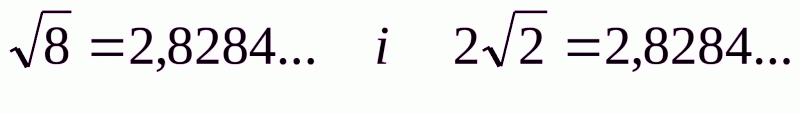 . Ці числа додатні, мають однакові цілі частини, однакові дробові частини, тому
. Ці числа додатні, мають однакові цілі частини, однакові дробові частини, тому 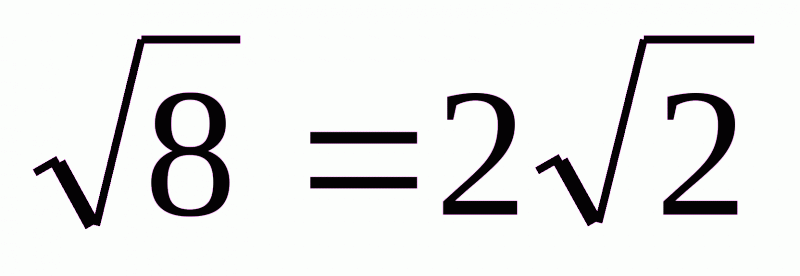 .
.
Якщо дійсні числа відрізняються знаками, або модулями, то вони не рівні. Наприклад, числа 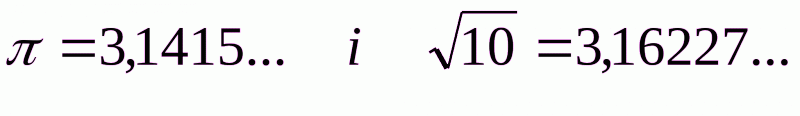 не дорівнюють одне одному, бо в них різні модулі. А яке ж з них більше? В них цілі частини однакові і десяті частини однакові, а соті різні. Перше число має менше сотих ніж друге тому
не дорівнюють одне одному, бо в них різні модулі. А яке ж з них більше? В них цілі частини однакові і десяті частини однакові, а соті різні. Перше число має менше сотих ніж друге тому  .
.
Порівняємо раціональне число з ірраціональним. Наприклад, 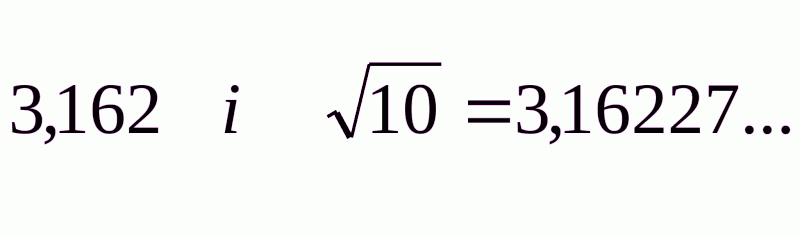 . Ці числа мають відповілно однакові цифри цілих, десятих, сотих і тисячних частин, а десятитисячних частин в першому немає (вважається, що цифра десятитисячних тут дорівнює 0), а в другому є 2 десятитисячних. Тому друге число більше від першого:
. Ці числа мають відповілно однакові цифри цілих, десятих, сотих і тисячних частин, а десятитисячних частин в першому немає (вважається, що цифра десятитисячних тут дорівнює 0), а в другому є 2 десятитисячних. Тому друге число більше від першого: 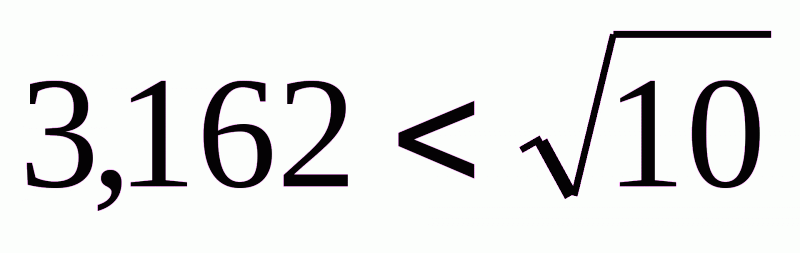 . Після таких прикладів учням корисно сформулювати висновки.
. Після таких прикладів учням корисно сформулювати висновки.
З двох дійсних додатних чисел більше те, в якого більша ціла частина, у випадку коли цілі частини рівні, коли десята частина більша і т. д. Порівняння дійсних чисел, з яких хоч одне від’ємне або нуль, виконують за такими самими правилами, які раніше були сформульовані для раціональних чисел. Будь-яке від’ємне число менше за будь-яке додатнє і нуль, з двох від’ємних чисел менше те у якого модуль більший.
Дії над дійсними числами.
Питання про дії над дійсними числами досить складне для учнів. Часто трапляється, що учитель дуже довго розглядає означення і правила цих дій, а в учнів залишаються від цього лише якісь туманні згадки.
В таких випадках краще пояснювати так:
-Ви ще раніше виконували дії над раціональними і ірраціональними числами. Проте тоді не з’ясовували, який зміст мають ці дії, не пояснювали, наприклад, що називається сумою двох дійсних чисел, коли хоч одне з них –ірраціональне число. Тепер розглянемо ці питання. Почнемо з додавання дійсних чисел.
Нехай, наприклад, треба додати два числа: 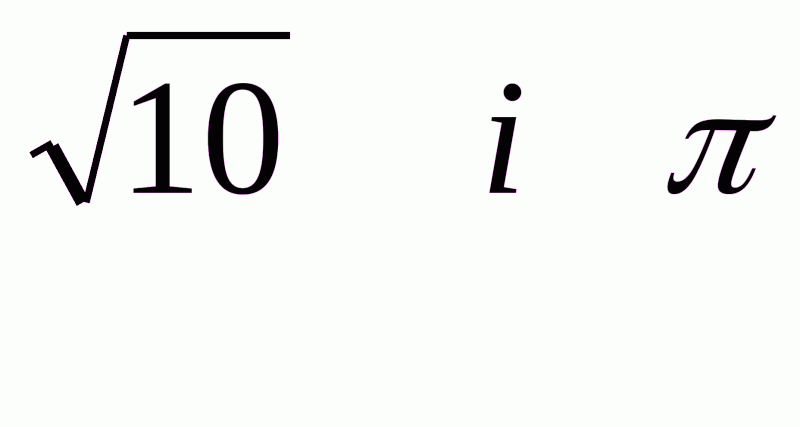 . З’єднаємо їх знаком “+” і дістанемо:
. З’єднаємо їх знаком “+” і дістанемо: 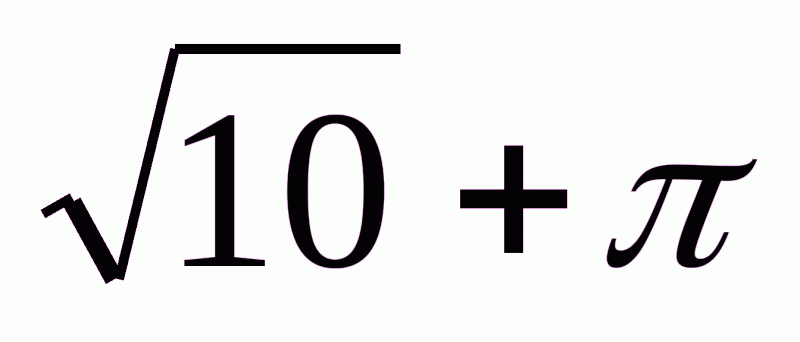 . Так записують суму чисел
. Так записують суму чисел 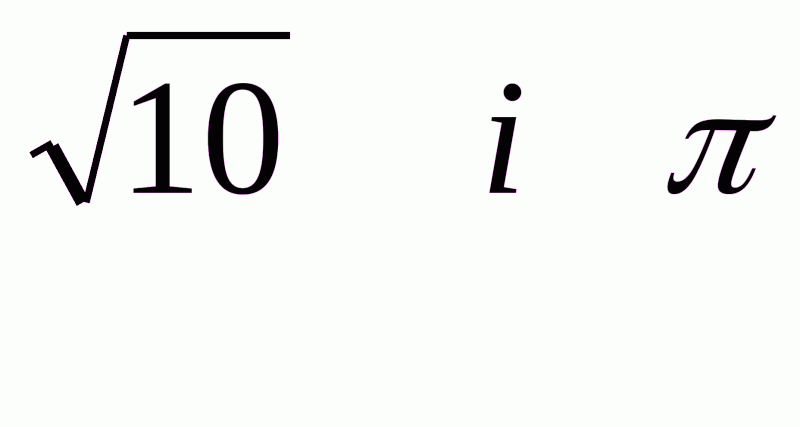 . Але що розуміють під сумою цих чисел? Під сумою двох дійсних чисел розуміють деяке дійсне число. Але яке саме? Щоб відповісти на це запитання, розглянемо десяткові наближення з недостачею і з надлишком кожного з доданків:
. Але що розуміють під сумою цих чисел? Під сумою двох дійсних чисел розуміють деяке дійсне число. Але яке саме? Щоб відповісти на це запитання, розглянемо десяткові наближення з недостачею і з надлишком кожного з доданків: 

Додамо наближене значення з недостачею числа  з будь-якою точністю і відповідне наближене значення з недостачею числа
з будь-якою точністю і відповідне наближене значення з недостачею числа  , дістанемо наближене значення суми
, дістанемо наближене значення суми 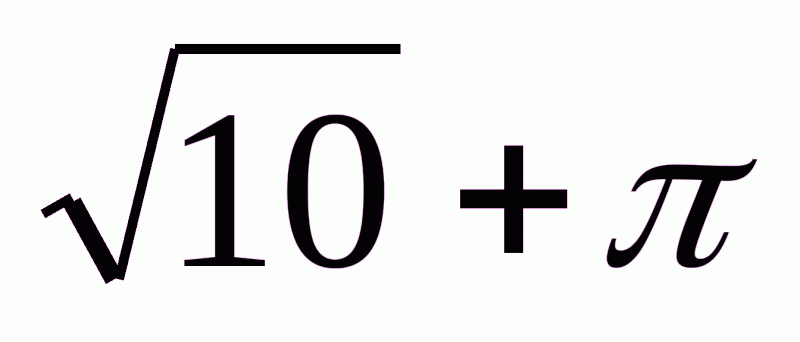 з недостачею. Випишемо послідовність таких наближених значень з недостачею: 6;6,2;6,30;6,303;6,3037;…
з недостачею. Випишемо послідовність таких наближених значень з недостачею: 6;6,2;6,30;6,303;6,3037;…
Аналогічно випишемо послідовність наближених значень з надлишком: 6;6,4;6,32;6,305;6,3039;…
Можна було б довести, що існує єдине дійсне число s, яке більше кожного з чисел першої послідовності і менше кожного з чисел другої. Число s і називається сумою даних чисел 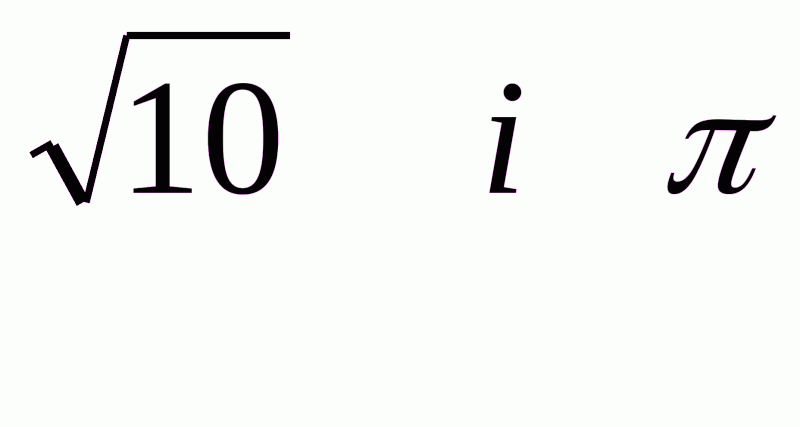 . Взагалі , сумою двох дійсних додатних чисел a і b називається таке третє число, яке більше від усіх сум відповідних десяткових наближень цих чисел з недостачею, але менше від усіх сум відповідних десяткових наближень цих чисел з надлишком.
. Взагалі , сумою двох дійсних додатних чисел a і b називається таке третє число, яке більше від усіх сум відповідних десяткових наближень цих чисел з недостачею, але менше від усіх сум відповідних десяткових наближень цих чисел з надлишком.
Далі слід зауважити без доведення, що так означена дія додавання дійсних чисел завжди можлива і однозначна, що для неї справедливі переставний і сполучний закони і, нарешті, що вона відповідає вже відомому учням додаванню відрізків. Якщо маємо два відрізки, довжини яких виражаються деякими дійсними числами a і b, то довжина третього відрізка, який дорівнює сумі двох перших, виражається дійсним числом, що дорівнює сумі чисел a і b.
Після таких пояснень учням варто зауважити, що при знаходженні суми дійсних чисел не треба кожного разу виписувати “трикутники чисел” і складати дві послідовності. Раніше це робилося тільки для того, щоб з’ясувати, що треба розуміти під сумою дійсних чисел. Знаходження наближених значень суми можна здійснювати за допомогою одноразового додавання відповідних наближень доданків. Наприклад, коли потрібно визначити з точністю до тисячних суму чисел 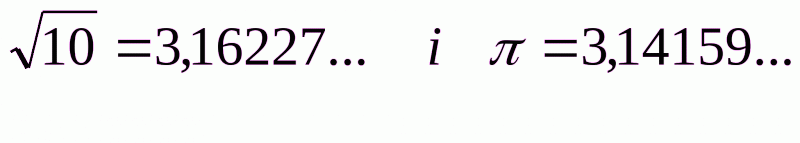 , то роблять так:
, то роблять так: 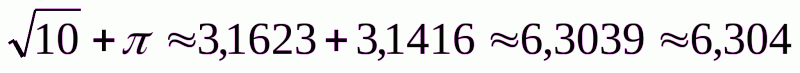 .
.
Аналогічно можна знайти наближене значення суми даних дійсних чисел з якою завгодно точністю, тільки для цього треба мати наближені значення доданків з достатньою точністю. Точні ж значення цієї суми виражаються нескінченним неперіодичним десятковим дробом.
Також корисно звернути увагу учнів на те, що в окремих випадках сума двох ірраціональних чисел може виражатися або скінченним, або нескінченним періодичним десятковим дробом. Наприклад, сума двох ірраціональних чисел 0,11011001100011… і 0,00100110011100… дорівнює 0,111111… , а це число раціональне. Але якщо одне з чисел ірраціональне, а друге раціональне, то їх сума завжди ірраціональне. Це можна довести методом від супротивного, враховуючи, що ніяке ірраціональне число не дорівнює раціональному.
Аналогічно можна розглянути й інші дії над дійсними числами. Проте довго спинятися на них не варто. Обов’язково слід зауважити, що додаючи, віднімаючи, множачи чи ділячи будь-які дійсні числа (в останньому випадку крім 0), ми щоразу в результаті дістаємо знову дійсне число, причому для додавання і множення цих чисел справджуються 5 відомих законів дій.
Обов’язково треба сказати учням, що між множиною дійсних чисел і точками числової прямої існує взаємно-однозначна відповідність: кожному лійсному числу відповідає єдина точка числової прямої і навпаки, кожній точці числової прямої відповідає єдине дійсне число. Цим множина дійсних чисел істотно відрізняється від всіх інших відомих учням числових множин.
Зрозуміло, що такий виклад розглядуваної теми далекий від строгого. Але строга теорія дійсних чисел досить складна і не входить в програму загальноосвітньої школи.
Висновки.
Отже, в результаті дослідницької діяльності і опрацювання наукової та методичної літератури, ми показали методику викладання теми “Дійсне число” у 8 класі. Після такого викладу матеріалу хотілося б, щоб учні почерпнули для себе цікаву інформацію, засвоїли основні поняття, зрозумілі принципи їх використання.
Обов’язковий результат навчання:
В результаті вивчення теорії учні повинні:
а) мати уявлення про раціональні, ірраціональні, дійсні числа;
б) знати означення раціонального числа, як звичайного дробу і як нескінченного періодичного дробу;
в) розуміти числову пряму як геометричну модель множини дійсних чисел;
г) знати про модуль дійсного числа, його властивості і геометричний зміст;
д) вивчити функцію виду y=|x|, її властивості і графік;
е) запам’ятати тотожність 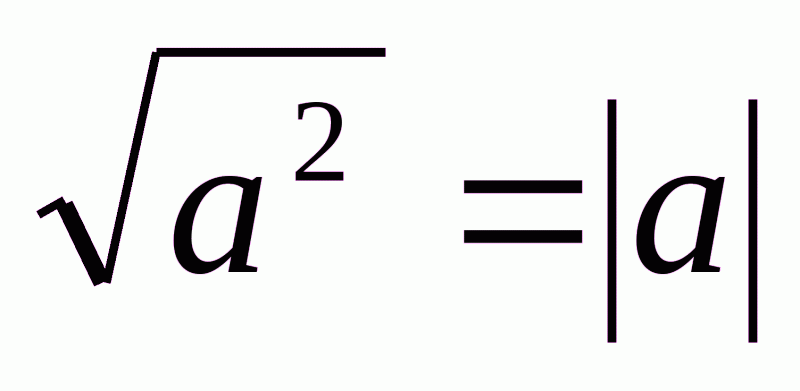 .
.
Практично набути вміння:
а) використання нових символів в математичний мові: N,Z,Q,R;
б) навести приклади раціональних і ірраціональних чисел, порівняти дійсні числа за величиною і розміщувати їх в порядку зростання на числовій прямій;
в) знаходити модуль буль-якого дійсного числа і використувувати його геометричний зміст для розв'язування простих рівнянь з модулем.
г) використовувати в нескладних випадках формулу 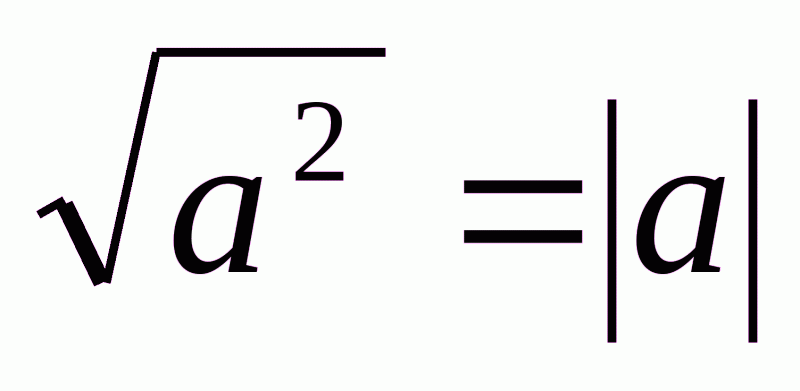 .
.
д) відшуковувати наближені значення дійсного числа із заданою точністю.
За одержаними результатами, можна говорити про майтерність вчителя; про його якості методиста.
Література.
Бевз Г.П. Методика викладання математики: Арифметика, алгебра, початки аналізу і геометрії.– К.: Вища школа, 1972.– 320 с.
Бевз Г.П. Методика викладання математики.– К.: Вища школа, 1989.– 366 с.
Бородін О.І. Історія розвитку поняття про число і системи числення.– К.: Рад. школа, 1963.– 69с.
Капіносов А.М. Алгебра 9 клас: заключне повторення. Тестова перевірка знань, умінь і навичок.– Дніпропетровськ: Дніпро, 1993.– 96 с.
Кованцов М.І. Математична хрестоматія: Алнебра і початки аналізу.– К.: Рад. школа, 1977.– 174 с.
Кушель О.В. Розвиток поняття про число. Ознаки подільності. Досконалі числа.– К.: Вища школа, 1974.– 50 с.
Макаричев Ю.М., Мигдюк Н.Г. та ін. Підручник: Алгебра 8 клас.– К.: Рад. школа, 1990.– 356 с.
Мордкович А.Г. Алгебра 8 клас: учебник.– М.: 1998.– 150с.
Мордкович А.Г. Методические рекомендации для учителя.– М.: 1998.– 72 с.
Рыбников К.А. Возникновение и развитие математической науки: Книга для учителя.– М.: Просвещение, 1987.– 86 с.
Фільчаков П.Ф. Довідник з елементарної математики для вступників до ВУЗів.– К.: Наукова думка, 1973.– 654 с.
Шарыгин И.Ф. Факультативный курс по математике: решение задач.– М.:Просвещение, 1989.– 352 с.
Додаток.
Як вже згадувалося, що на вивчення теми “дійсні числа” за програмою відведена дуже мала кількість годин. Тому доцільно було б для її закріплення провести факультативне заняття (присутність всіх учнів класу обов’язкова).
Факультативне заняття.
Тема: Дійсні числа.
Мета заняття: закріпити вивчений на уроці матеріал та виробити уміння і навички роботи з дійсними числами.
В структурі заняття виділимо 2 частини:
1). Коротке повторення теоретичного матеріалу;
2). розв'язування задач на дану тему.
Отже, згідно визначеного плану роботи повторимо вивчений матеріал.
Згадаємо, що якщо доповнити множину цілих чисел дробовими, то одержимо множину раціональних чисел. Яке число називається раціональним?
(учні). Раціональними називаються числа, які можна подати у вигляді дробу  , де p і q – цілі. Цілі числа згідно цього означення можна розглядати як
, де p і q – цілі. Цілі числа згідно цього означення можна розглядати як 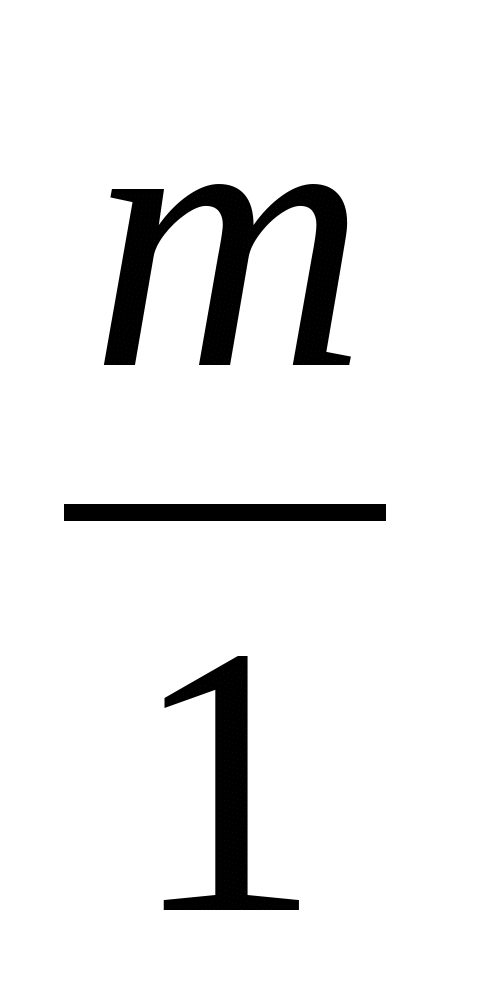 , де m – ціле.
, де m – ціле.
Ми розглянули доповнення множини раціональних чисел ірраціональними. Які числа ірраціональні?
(учні) Ірраціональні числа – це числа які виражаються нескінченним неперіодичним дробом.
В результаті одержали множину дійсних чисел, яка заповнює так звану числову пряму. Нагадаємо, що звичайна пряма стає числовою, якщо на ній позначити 2 точки: 0 і 1. Тепер встановилася взаємно однозначна відповідність між точками прямої і дійсними числами.
Розглянемо основні типи задач, які пов’язані з теорією дійсного числа.
Одним із поширених типів задач є задачі на доведення ірраціональності даного числа.
№1. Довести ірраціональність числа 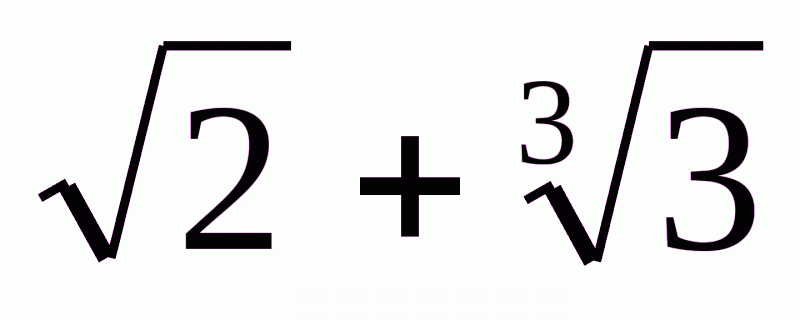 .
.
Розв'язання. Припустимо протилежне: 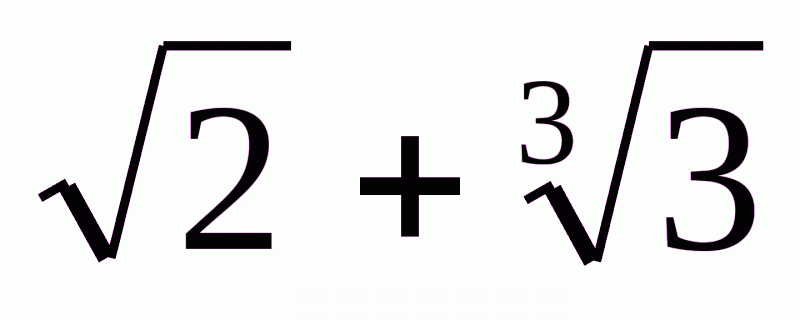 =r, де r – раціональне число. Тоді
=r, де r – раціональне число. Тоді 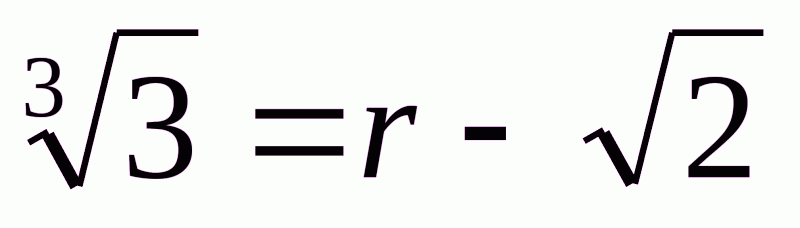 . Піднесемо до кубу:
. Піднесемо до кубу:  . Звідси,
. Звідси, 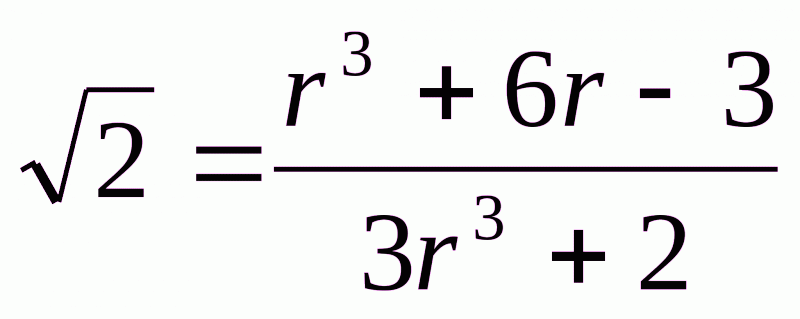 . Одержали, що
. Одержали, що 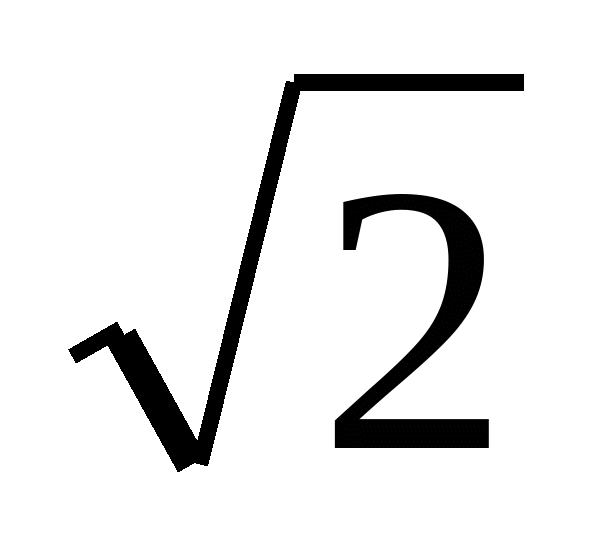 рівне раціональному числу, а це протиріччя і доводить задачу.
рівне раціональному числу, а це протиріччя і доводить задачу.
Другий тип задач – це порівняння дійсних чисел.
№2. Порівняти, що більше  .
.
Розв'язання.
Нехай 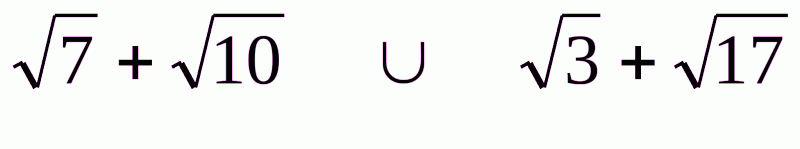 . Піднесемо обидві частини до квадрата, віділяємо один корінь, знову підносимо до квадрату:
. Піднесемо обидві частини до квадрата, віділяємо один корінь, знову підносимо до квадрату: .
.
Тут очевидно, що 67<12.7<12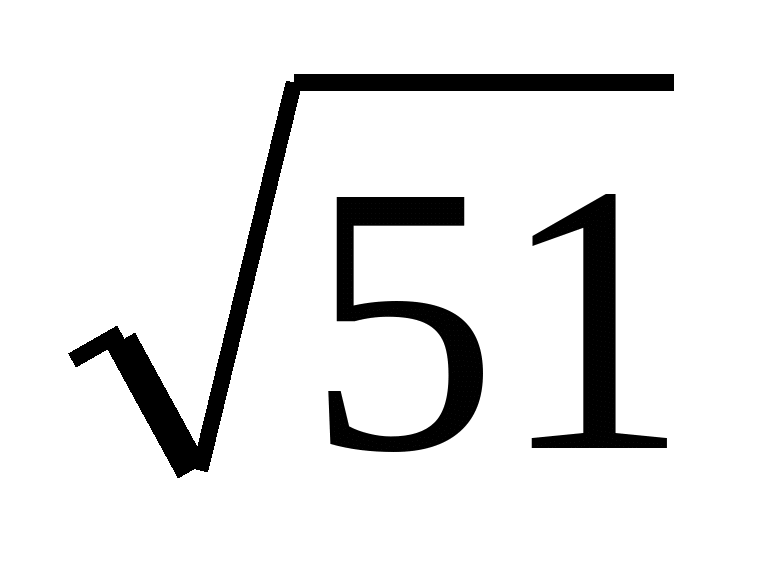 .
.
Звідси  .
.
Тест.
1. Які з даних чисел: 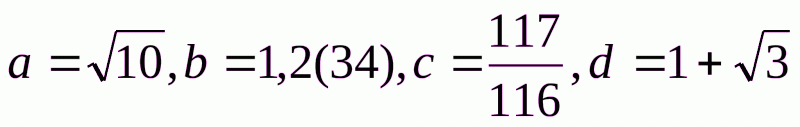 , є ірраціональні.
, є ірраціональні.
A. a,b,c. Б. a,d. В. c,b. Г.а.
2. Розмістіть числа  , в порядку зростання.
, в порядку зростання.
А. a, b, c. Б. b, c, a. B. c, a, b. Г. a, c, b.
3. Яке із даних співвідношень є правильною числовою рівністю.
А.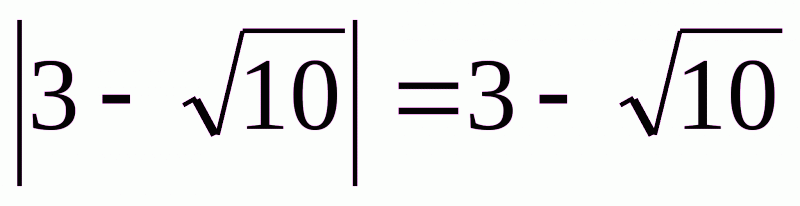 .
.
Б.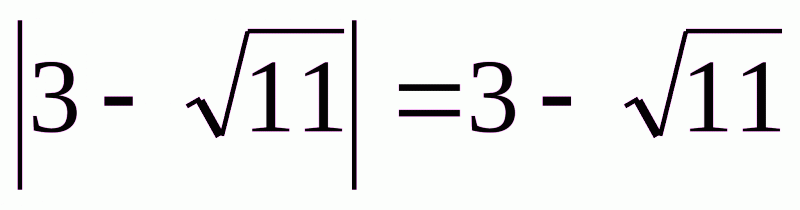 .
.
В. 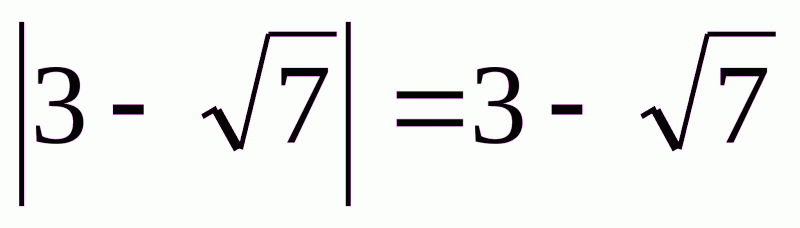 .
.
Г.  .
.
4. Спростіть вираз 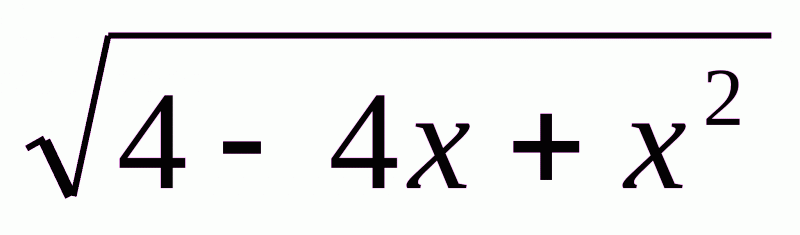 , якщо відомо, що
, якщо відомо, що 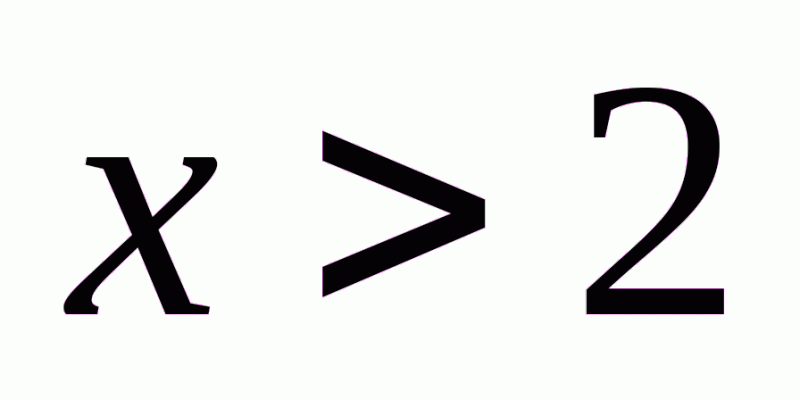 .
.
А. 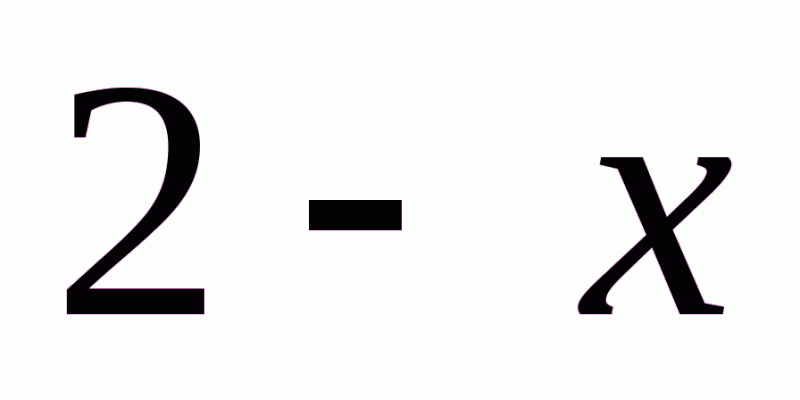 . Б.
. Б. 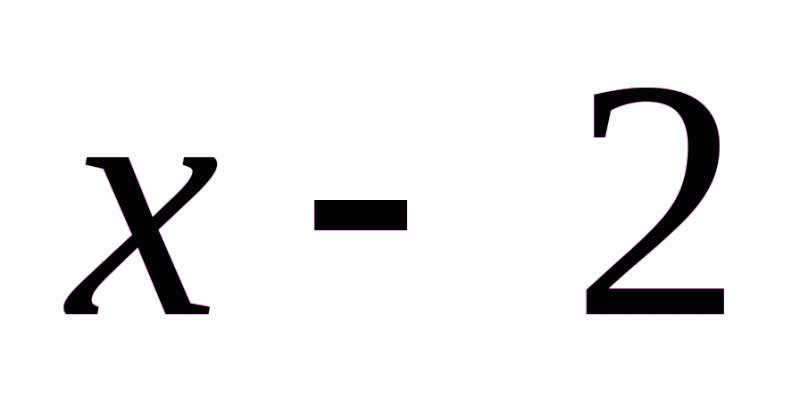 .В.
.В. 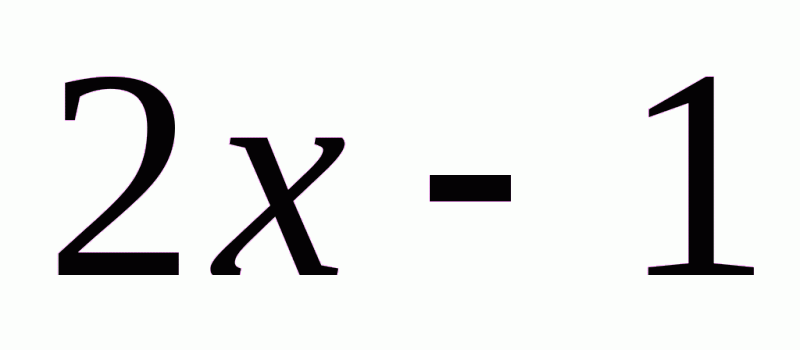 . Г.
. Г. 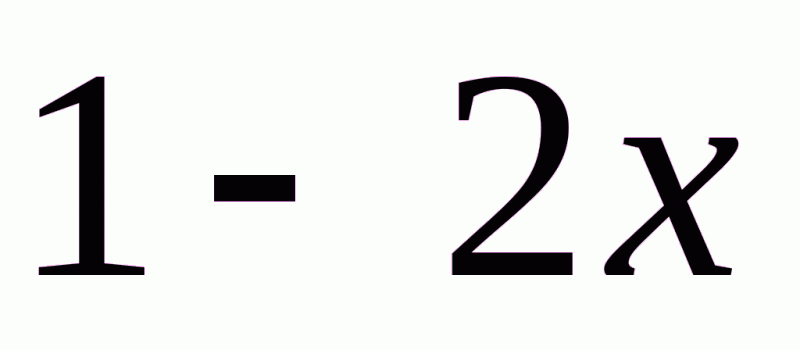 .
.
5. Чому рівні числа  ;
; ;
;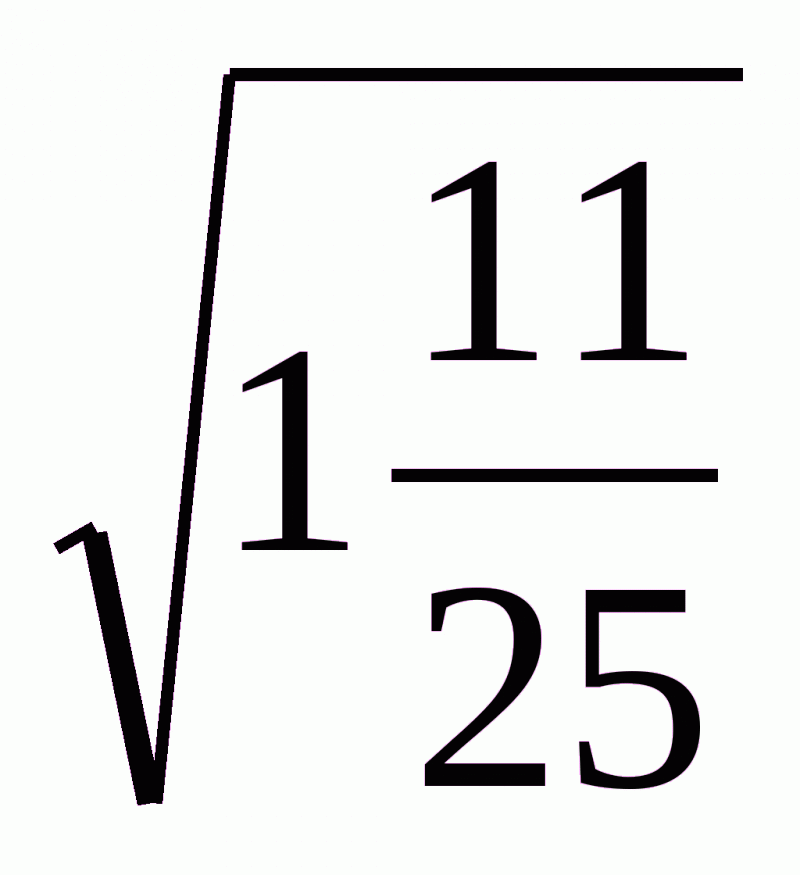 .
.
А. 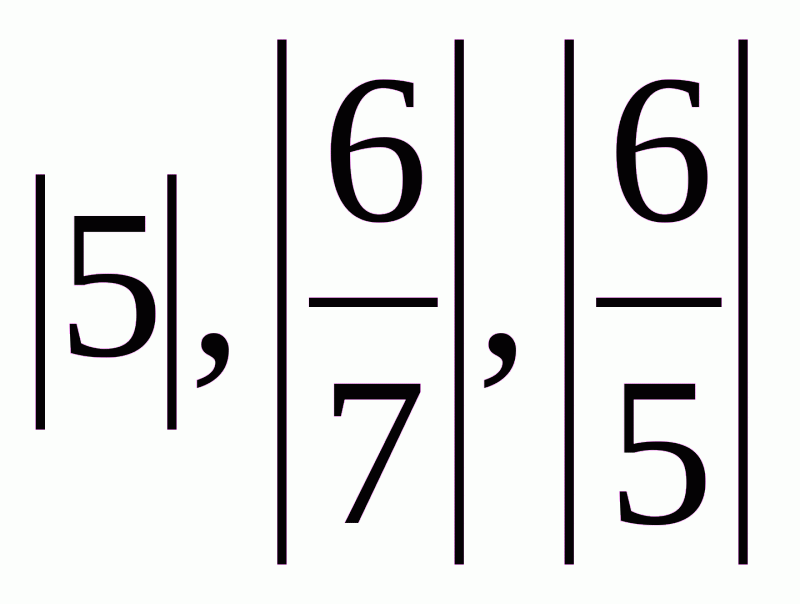 , Б.
, Б. , В.
, В.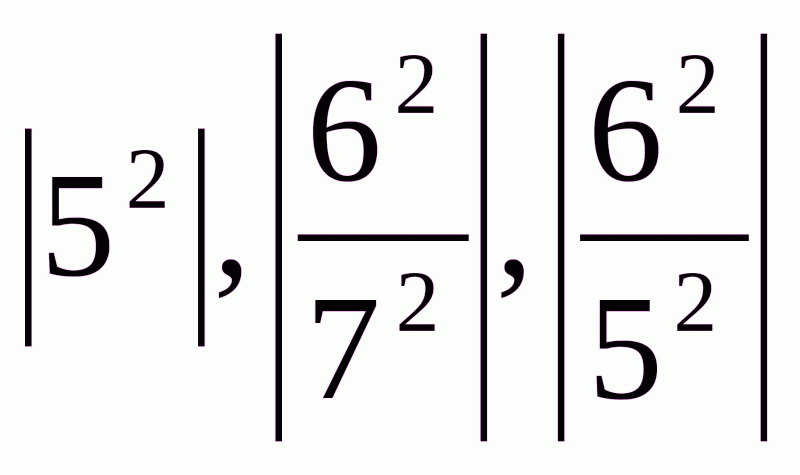 .
.
Код правильних відповідей: Б, Г, В, Б, А.
Учні підсумовують собі бали: 1 бал за кожне правильно розв’язане завдання.
Цей тест, в основному, виявить міру засвоєності ноаого матеріалу і допоможе вчителеві звернути увагу на ті питання, які викликають труднощі у учнів.
Тепер перейдемо до другої частини нашого заняття, тобто будемо розв'язувати різноманітні завдання.
№1. Даний періодичний дріб. Представити його у вигляді дробу виду  : а) 0,(27), б) 0,(481).
: а) 0,(27), б) 0,(481).
Розв'язання.
а) число х=0,27. Тоді _100х=27,272727…
х=0,272727…
99х=27, 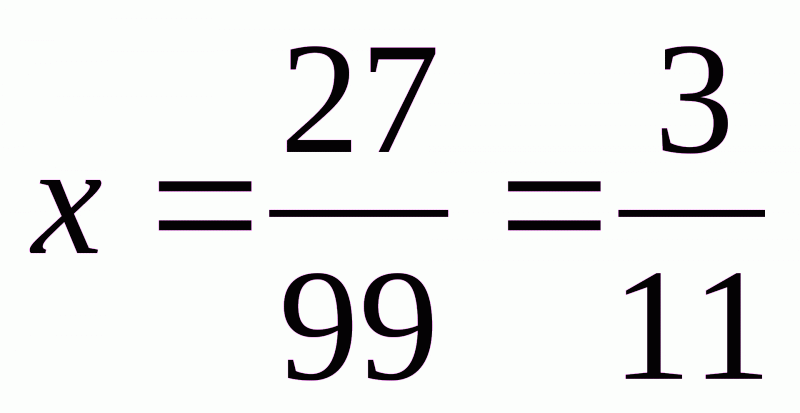 . Звідси
. Звідси 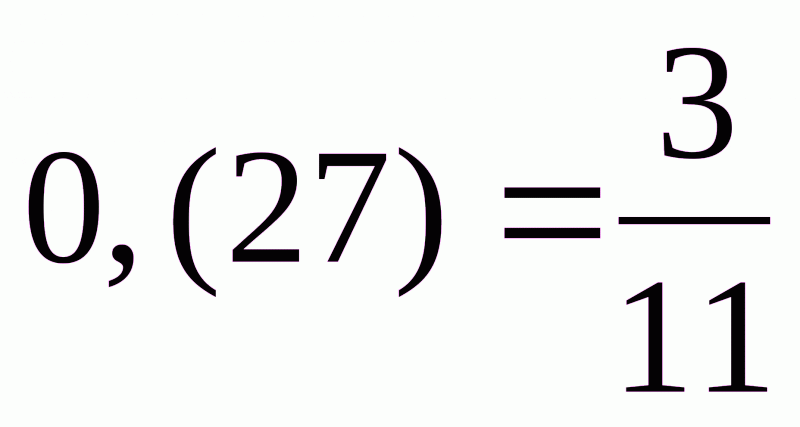 .
.
б) 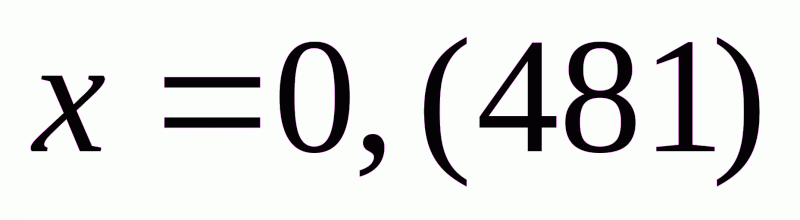 . Тоді одержимо:
. Тоді одержимо:
_ 1000х=481,481481…
х=0,481481...
999х=481, то звідси 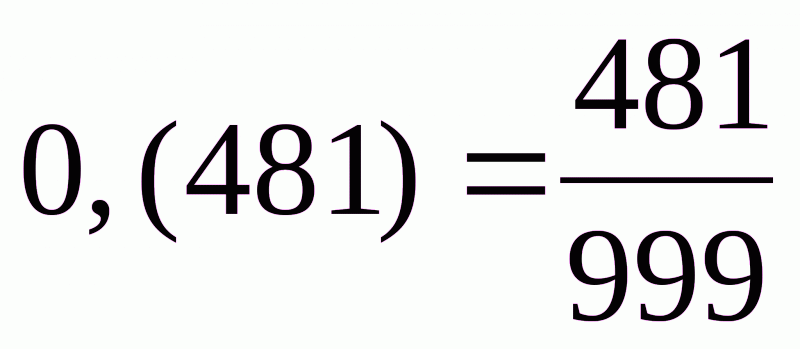 .
.
№2 Доведіть ірраціональність числа 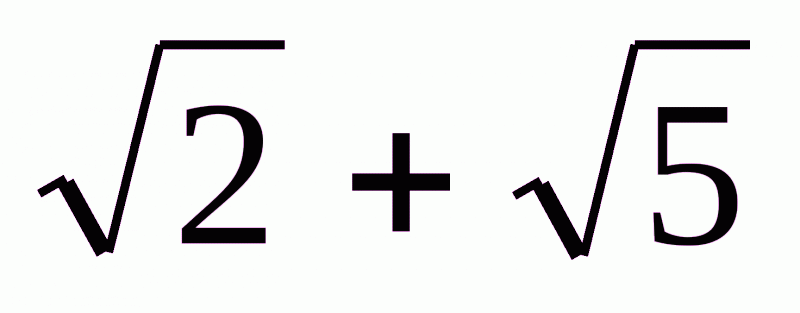 .
.
Розв'язання.
Нехай 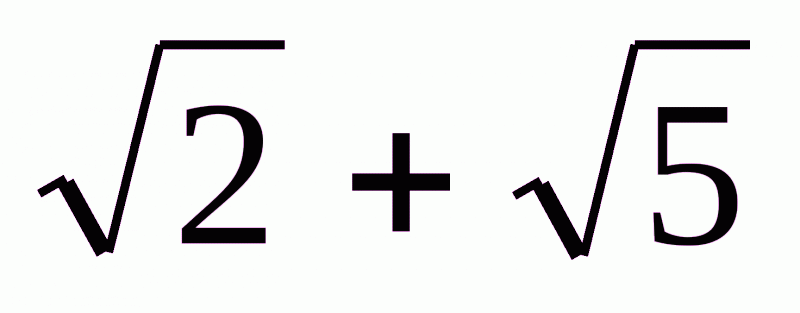 =r – раціональне число. Піднесемо його до квадрата і перетворимо
=r – раціональне число. Піднесемо його до квадрата і перетворимо 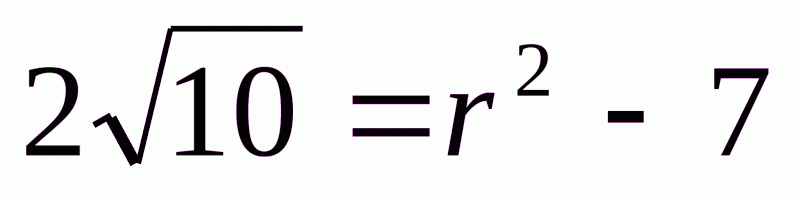 . Звідси,
. Звідси, 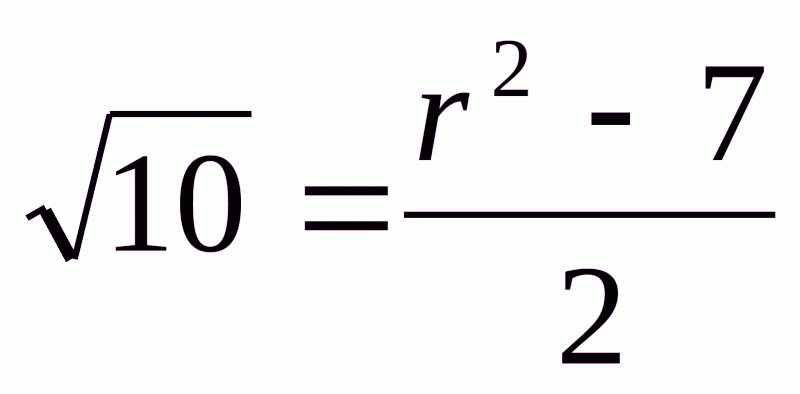 . Це означає, що
. Це означає, що 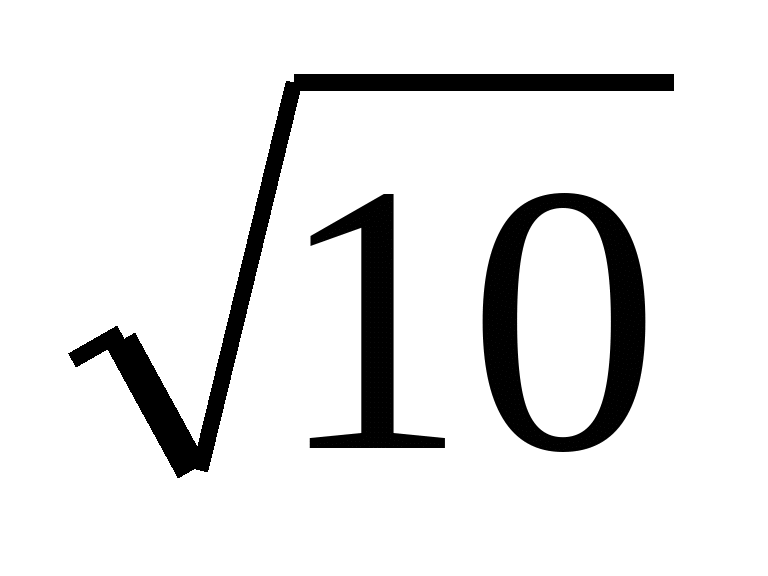 рівний раціональному числу, що невірно, бо
рівний раціональному числу, що невірно, бо 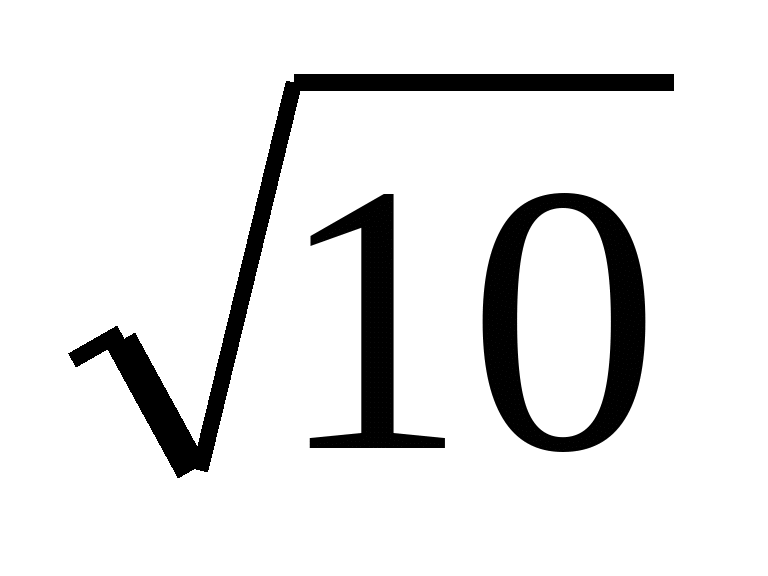 ірраціональне число. Отже
ірраціональне число. Отже 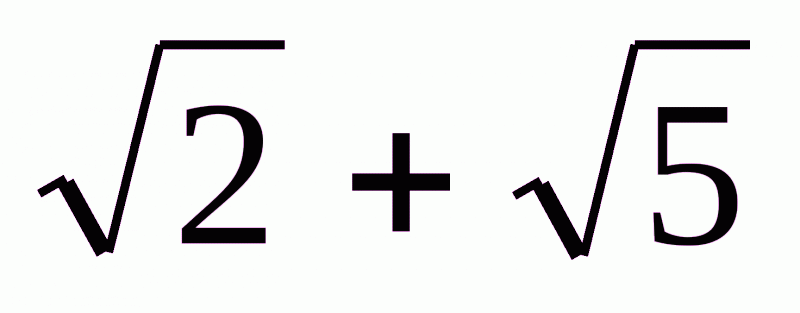 ірраціональне число.
ірраціональне число.
№3. Розв'язати рівняння: а) 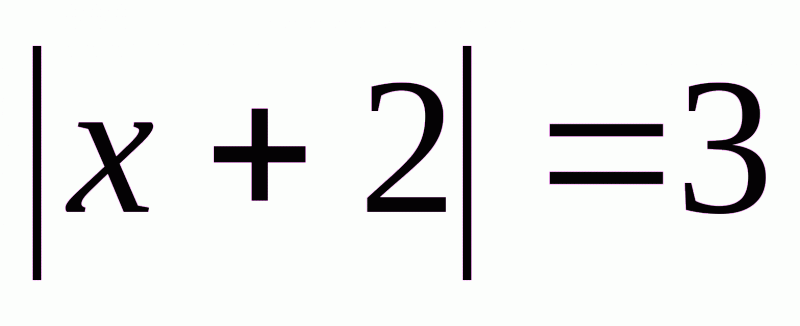 ; б)
; б)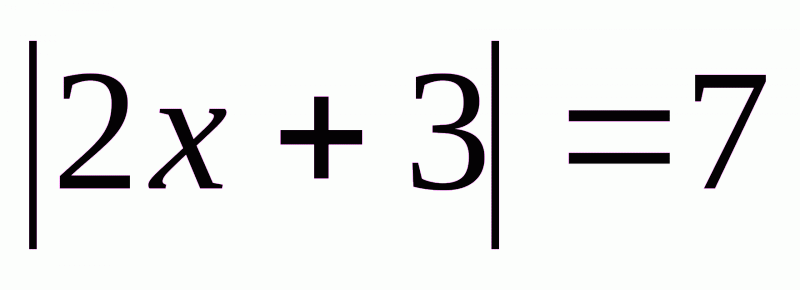 .
.
Розв’язання.
А) Якщо 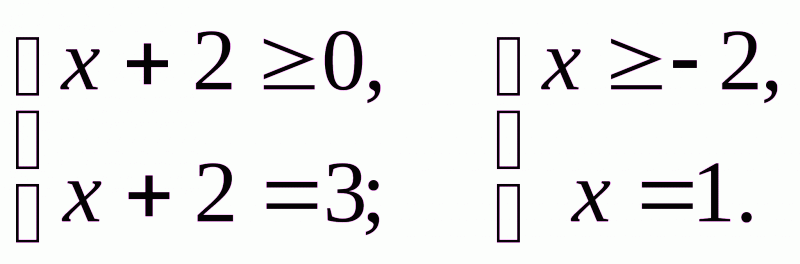 Якщо
Якщо 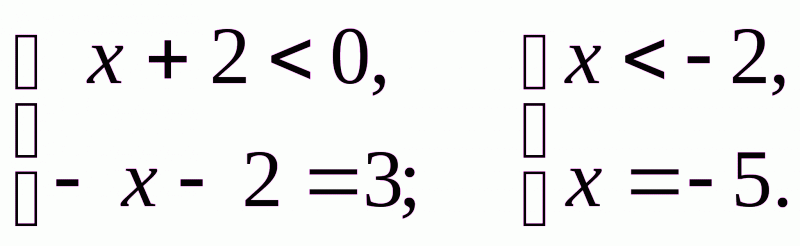
Відповідь: 1 або –5.
Б) Якщо  ,якщо
,якщо 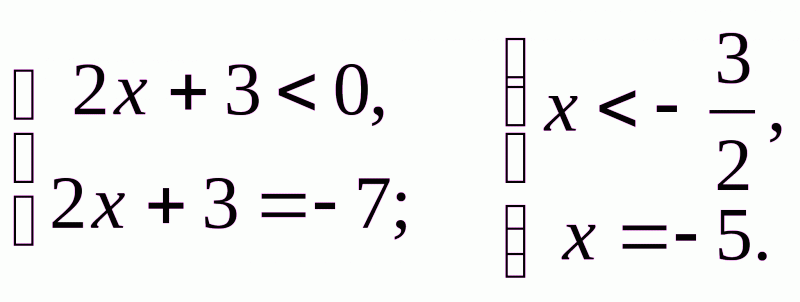
Відповідь. 2 або –5.
№4 Спростити вираз 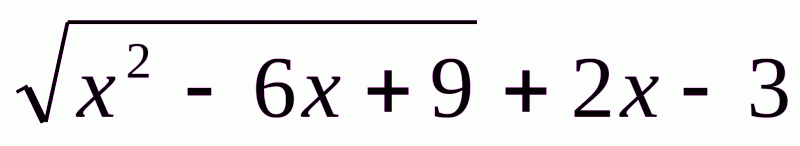 , якщо відомо, що
, якщо відомо, що  .
.
Розв’язання.  , оскільки
, оскільки  , то
, то 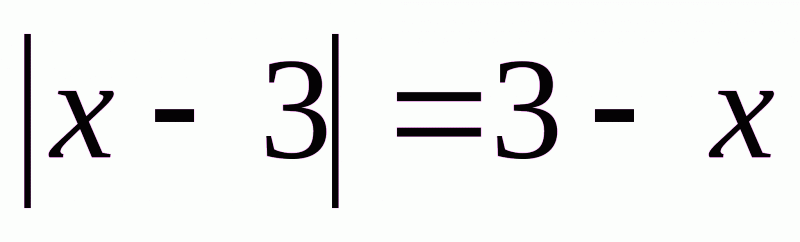 ,
,
 .
.
№5. Спростити вираз 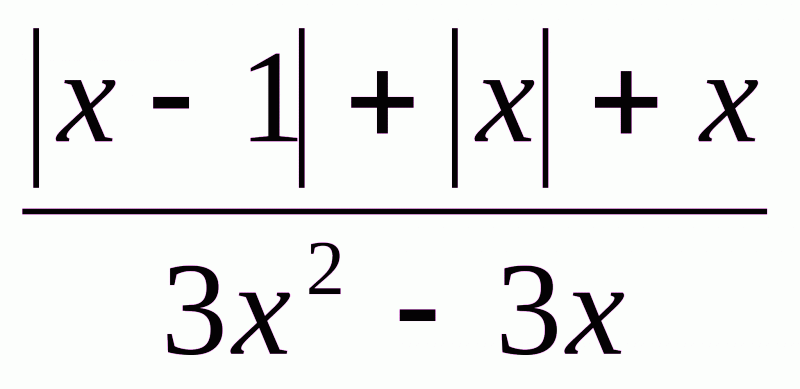 , якщо
, якщо
а) 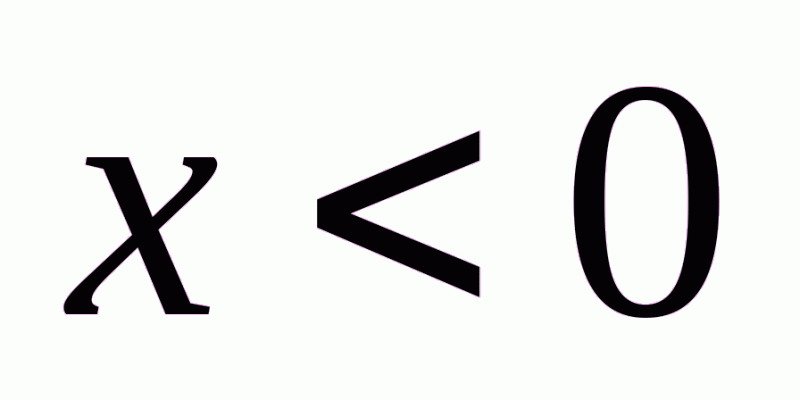 , б)
, б) 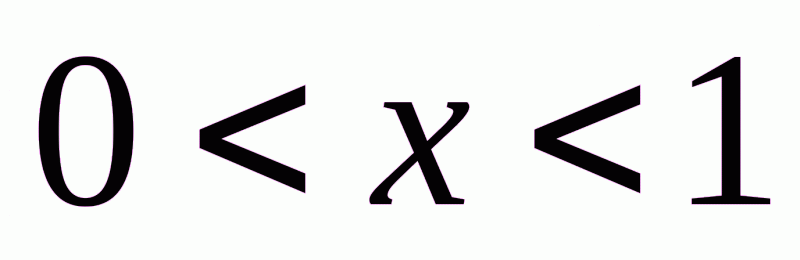 , в)
, в) 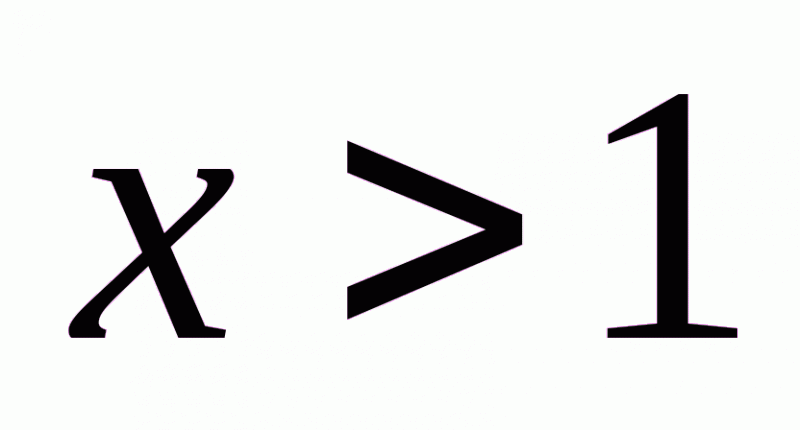 .
.
Розв’язання
а) Якщо 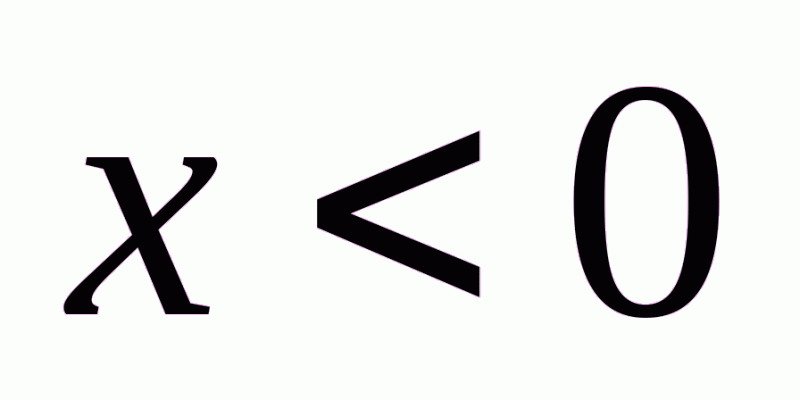 , то
, то 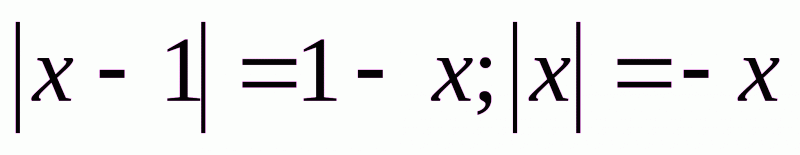 . Тоді
. Тоді 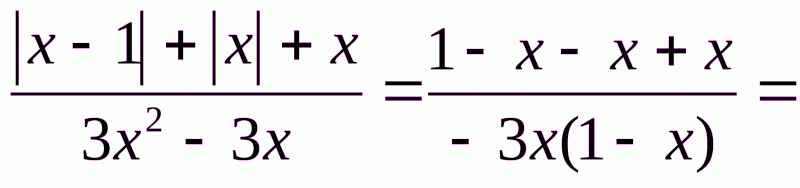
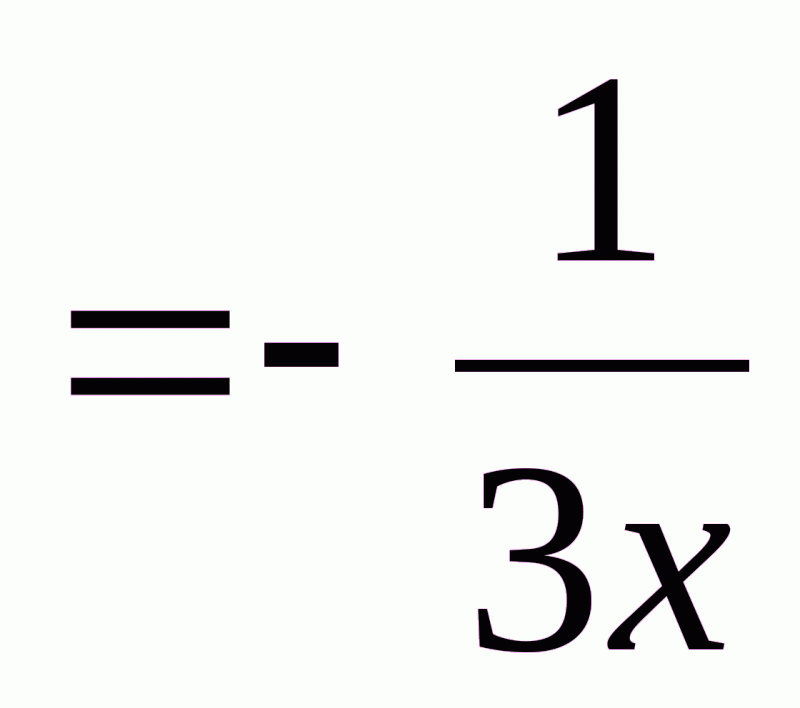 .
.
б) якщо 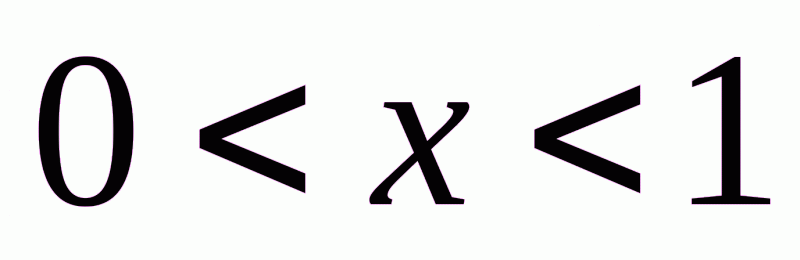 , то
, то 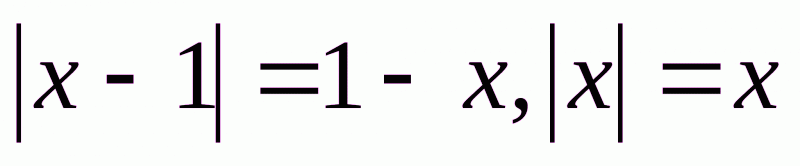 . Тоді
. Тоді

в) якщо 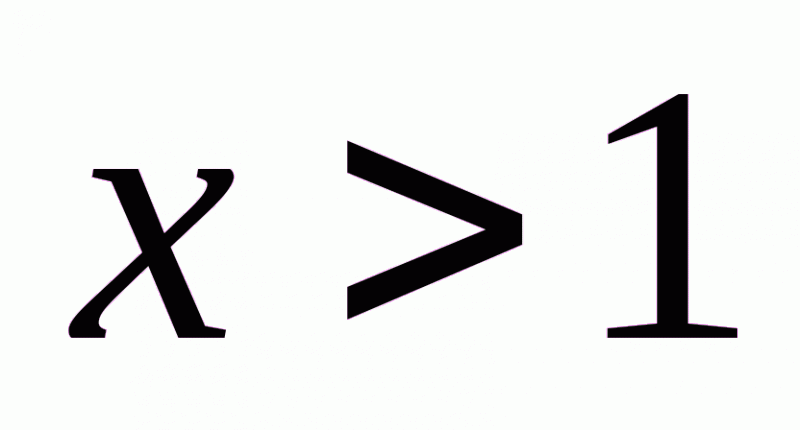 , то
, то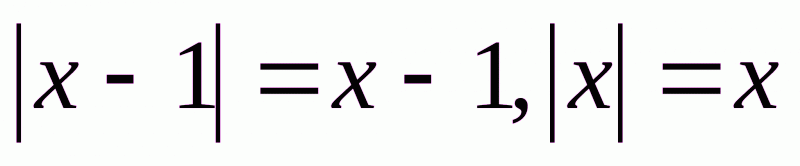 . Тоді
. Тоді
 .
.
№6 Побудувати графік функції 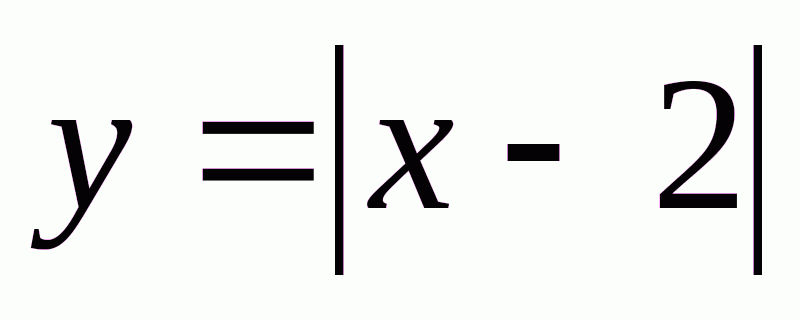 .
.
Якщо 
Якщо 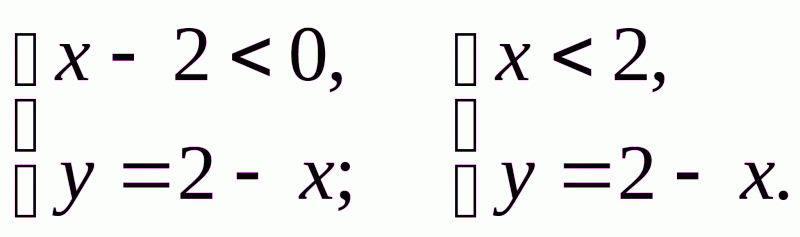
Т обто, при
обто, при  побудуємо пряму
побудуємо пряму 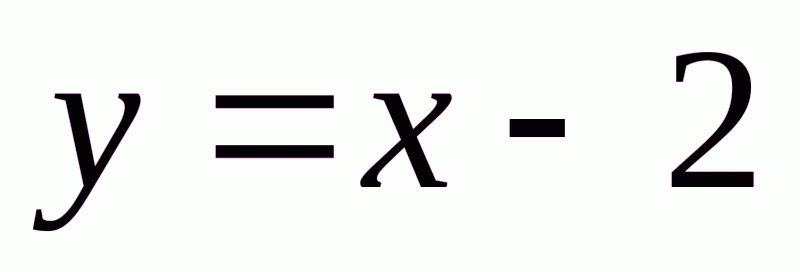 , а при
, а при  побудуємо пряму
побудуємо пряму 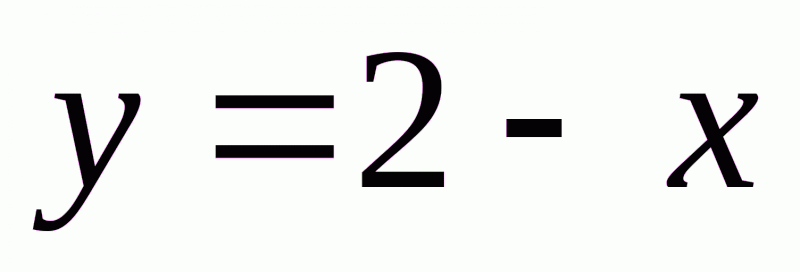 .
.
На цьому занятті ми розглянули основні типи задач на тему “Дійсні числа”. Навчилися доводити ірраціональність чисел, порівнювати дійсні числа, розв’язувати рівняння з модулями, користуючись його означення.
Заняття закінчено.

