КУРСОВАЯ РАБОТА ПО ФИЗИКЕ:
ЧЕРНЫЕ ДЫРЫ.
СОДЕРЖАНИЕ.
ВВЕДЕНИЕ.
ОБРАЗОВАНИЕ ЧЕРНЫХ ДЫР. ГРАВИТАЦИОННЫЙ КОЛЛАПС. ГРАВИТАЦИОННЫЙ РАДИУС.
КВАНТОВОЕ ИЗЛУЧЕНИЕ ЧЕРНЫХ ДЫР.
ТЕРМОДИНАМИКА ЧЕРНЫХ ДЫР.
ЧЕРНЫЕ ДЫРЫ И ТЕРМОДИНАМИКА.
ТЕМПЕРАТУРА И ЭНТРОПИЯ ЧЕРНОЙ ДЫРЫ.
ТЕРМОДИНАМИКА И ИНФОРМАЦИЯ.
ИНФОРМАЦИООНЫЙ ПОДХОД К ТЕРМОДИНАМИКЕ.
ЭНТРОПИЯ И ИНФОРМАЦИЯ.
ЧЕРНЫЕ ДЫРЫ И ВРЕМЯ.
ЭФФЕКТ ЗАМЕДЛЕНИЯ ВРЕМЕНИ НА ПОВЕРХНОСТИ ЧЕРНОЙ ДЫРЫ.
КВАНТ ПРОСТРАНСТВА - ВРЕМЕНИ НА ПОВЕРХНОСТИ ЧЕРНОЙ ДЫРЫ.
ТИПЫ ЧЕРНЫХ ДЫР.
ЗАКЛЮЧЕНИЕ.
СПИСОК ЛИТЕРАТУРЫ.
ВВЕДЕНИЕ.
Черные дыры – объекты совершенно фантастические по своим свойствам. « Из всех измышлений человеческого ума, от единорогов и химер до водородной бомбы, наверное, самое фантастическое – это образ черной дыры, отделенной от остального пространства определенной границей, которую ничто не может пересечь; дыры, обладающей настолько сильным гравитационным полем, что даже свет задерживается его мертвой хваткой; дыры, искривляющей пространство и тормозящей время. Подобно единорогам и химерам, черная дыра кажется более уместной в фантастических романах или в мифах древности, чем в реальной Вселенной. И, тем не менее, законы современной физики фактически требуют, чтобы черные дыры существовали. Возможно, только наша Галактика содержит их» - так сказал о черных дырах американский физик К. Торн.
К этому следует добавить, что внутри черной дыры удивительным образом меняются свойства пространства и времени, закручивающихся в своеобразную воронку, а в глубине находится граница, за которой время и пространство распадаются на кванты… Внутри черной дыры, за краем этой своеобразной гравитационной бездны, откуда нет выхода, текут удивительные физические процессы, проявляются новые законы природы.
Черные дыры являются самыми грандиозными источниками энергии во Вселенной. Мы, вероятно, наблюдаем их в далеких квазарах, во взрывающихся ядрах галактик. Они возникают также после смерти больших звезд. Возможно, черные дыры в будущем станут источниками энергии для человечества.
ОБРАЗОВАНИЕ ЧЕРНЫХ ДЫР. ГРАВИТАЦИОННЫЙ КОЛЛАПС. ГРАВИТАЦИОННЫЙ РАДИУС .
Ученые установили, что черные дыры должны возникать в результате очень сильного сжатия какой-либо массы, при котором поле тяготения возрастает настолько сильно, что не выпускает ни свет, ни какое-либо другое излучение, сигналы или тела.
Еще в 1798 г. П. Лаплас, исследуя распространение света в поле тяготения объекта, большая масса которого сосредоточена внутри малой области пространства, пришел к заключению, что в природе могут встречаться тела абсолютно черные для внешнего наблюдателя. Поле тяготения таких тел настолько велико, что не выпускает наружу лучей света (на языке космонавтики это означает, что вторая космическая скорость была бы больше скорости света с ). Для этого необходимо лишь, чтобы масса объекта М была сосредоточена в области с радиусом, меньшим так называемого гравитационного радиуса тела Rg . Радиус
Rg =2 GM / c ² » 1,5*10-28 М, где G -постоянная тяготения;
М- масса (измеряется в граммах) ,
Rg -в сантиметрах.
Вывод Лапласа основывался на классической механике и теории тяготения Ньютона1 .
Следовательно, для возникновения черной дыры необходимо, чтобы масса сжалась до таких размеров, при которых вторая космическая скорость становится равной скорости света. Этот размер носит название гравитационного радиуса и зависит от массы тела. Величина его очень мала даже для масс небесных тел. Так, для Земли гравитационный радиус приблизительно равен 1см, для Солнца – 3 км.
Для того чтобы преодолеть тяготение и вырваться из черной дыры, потребовалась бы вторая космическая скорость, большая световой. Согласно теории относительности , никакое тело не может развивать скорость большую, чем скорость света. Вот почему из черной дыры ничто не может вылететь, не может поступать наружу никакая информация. После того как любые тела, любое вещество или излучение упадут под действием тяготения в черную дыру, наблюдатель никогда не узнает, что произошло с ними в дальнейшем. Вблизи черных дыр, как утверждают ученые, должны резко изменяться свойства пространства и времени.
Если черная дыра возникает в результате сжатия вращающегося тела, то вблизи ее границы все тела вовлекаются во вращательное движение вокруг нее.
Ученые считают, что черные дыры могут возникать в конце эволюции достаточно массивных звезд. После исчерпания запасов ядерного горючего звезда теряет устойчивость и под действием собственной гравитации начинает быстро сжиматься. Происходит так называемый гравитационный коллапс (такой процесс сжатия, при котором силы тяготения неудержимо возрастают).
А именно, к концу жизни звезды теряют массу в результате целого ряда процессов: звездного ветра, переноса массы в двойных системах, взрыва сверхновых и т.д.; однако известно, что существует много звезд с массой, в 10, 20 и даже в 50 раз превышающей солнечную. Маловероятно, что все эти звезды как-то избавятся от «излишней» массы, чтобы войти в указанные пределы (2-3М- ). Согласно теории, если звезда или ее ядро с массой выше указанного предела начинает коллапсировать под действием собственной тяжести, то ничто уже не в состоянии остановить ее коллапс. Вещество звезды будет сжиматься беспредельно, в принципе, пока не сожмется в точку. В ходе сжатия сила тяжести на поверхности неуклонно возрастает – наконец, наступает момент, когда даже свет не может преодолеть гравитационный барьер. Звезда исчезает: образуется то, что мы называем ЧЕРНОЙ ДЫРОЙ.
КВАНТОВОЕ ИЗЛУЧЕНИЕ ЧЕРНЫХ ДЫР.
Утверждение, что конечное состояние черной дыры стационарно, правильно лишь в рамках обычной, не квантовой теории тяготения. Квантовые эффекты ведут к тому, что на самом деле черная дыра должна непрерывно излучать, теряя при этом свою энергию.1
 Поле тяготения черной дыры очень велико (именно поэтому оно производит над падающим телом работу, соизмеримую с его энергией покоя). Рассматривая чисто динамическую задачу о рождении частиц в таком гравитационном поле, С. Хокинг в 1975 г. показал, что оно делает физический вакуум2
неустойчивым: всегда присутствующие в нем виртуальные (короткоживущие) частицы превращающиеся в реальные (долгоживущие). Точнее говоря, в вакууме вблизи горизонта событий3
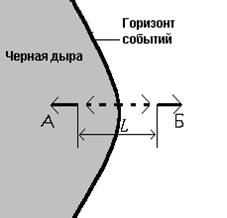
поле рождает пары частиц, причем одна из компонент пары уходит внутрь черной дыры, занимая состояние с отрицательной энергией, а другая, имеющая положительную энергию, вылетает наружу и может быть зарегистрирована далеким наблюдателем (рис. 1).
Поле тяготения черной дыры очень велико (именно поэтому оно производит над падающим телом работу, соизмеримую с его энергией покоя). Рассматривая чисто динамическую задачу о рождении частиц в таком гравитационном поле, С. Хокинг в 1975 г. показал, что оно делает физический вакуум2
неустойчивым: всегда присутствующие в нем виртуальные (короткоживущие) частицы превращающиеся в реальные (долгоживущие). Точнее говоря, в вакууме вблизи горизонта событий3
поле рождает пары частиц, причем одна из компонент пары уходит внутрь черной дыры, занимая состояние с отрицательной энергией, а другая, имеющая положительную энергию, вылетает наружу и может быть зарегистрирована далеким наблюдателем (рис. 1).
Рис.1. Рождение пары в поле черной дыры.
В вакууме постоянно рождаются и аннигилируют пары виртуальных частиц, которым, однако, не хватает энергии для превращения в реальные долгоживущие частицы. В достаточно сильном внешнем поле этот недостаток энергии может быть восполнен работой, производимой полем над частицами. Для появления реальной пары с энергией Е (сплошные линии) необходимо, чтобы ее компоненты, находясь еще в виртуальном состоянии (пунктир), разошлись на расстояние L, на котором работа поля равна Е. Одна из компонент пары (А) падает внутрь черной дыры, (Б) уходит наружу, к внешнему наблюдателю. Совокупность частиц Б и есть излучение Хокинга.
Таким образом, квантовые свойства вакуума проявляются в том, что черная дыра «обязана» излучать частицы разных сортов, в том числе кванты света. Изучая свойства этого излучения, Хокинг пришел к неожиданному заключению, что оно имеет тепловой характер: черная дыра светит точно так же, как черное тело радиуса Rg , нагретого до температуры
θ =ћ c ³/8 πkMG ≈1026 / M ,
где ћ - постоянная Планка;
k -постоянная Больцмана;
θ - температура (измеряется в градусах Кельвина);
М-масса в граммах.
При этом не только спектр излучения (распределение его по частотам), но и более тонкие его характеристики (например, все корреляционные функции) точно такие же, как у излучения черного тела.
ТЕРМОДИНАМИКА ЧЕРНЫХ ДЫР.
ЧЕРНЫЕ ДЫРЫ И ТЕРМОДИНАМИКА .
Открытие теплового излучения черной дыры было полной неожиданностью для большинства специалистов.
Дж. Уилер первым обратил внимание на то, что в рамках классической теории тяготения уже сам факт существования черной дыры противоречит второму началу термодинамики, согласно которому полная энтропия физической системы - величина, характеризующая степень ее хаотичности, или растет со временем, или по крайней мере остается постоянной. Например, когда внутрь черной дыры падает горячее тело, обладающее некоторым запасом энтропии, в результате чего внешний наблюдатель видит уменьшение полной энтропии мира, доступного его наблюдению. На это можно возразить, сказав, что «на самом деле» противоречия с термодинамикой нет, так как увеличилась энтропия внутренней части черной дыры. Это действительно так но только для наблюдателя, падающего вместе с горячим телом, который не столкнется ни с нарушением термодинамики, ни с самим эффектом Хокинга. Однако системой отсчета внешнего наблюдателя внутренняя часть черной дыры вообще не охватывается. Поэтому для такого наблюдателя упавшее в дыру тело реально исчезает (передавая, конечно, черной дыре как целому свои сохраняющиеся характеристики – энергию, или массу М , вращательный момент J и заряд Q) .
Эти соображения приводят к следующей дилемме: либо термодинамика вообще запрещает существование черных дыр, либо этот объект сам по себе обладает запасом доступной наблюдению извне энтропии, которая возрастает после падения на него горячего тела. Вторая возможность, которая и оказалась правильной, означает, что такое тело передает черной дыре как целому не только М , момент J и заряд Q , но и свою энтропию.
Однако еще раньше, чем был сделан выбор в пользу этой возможности, появилось довольно много теоретических указаний на то, что свойства одной из характеристик черной дыры – площади ее поверхности – действительно напоминают свойства энтропии. Одно из таких указаний относится к процессам естественной эволюции черной дыры – аккреции вещества на нее, слиянию двух черных дыр в одну и т.п. при полном отсутствии обратных процессов. Оказывается, с течением времени суммарная площадь поверхности черных дыр, как и энтропия, либо возрастает, либо, в крайнем случае, остается постоянной1 .
Вообще оказалось, что аналогия между физикой черных дыр и термодинамикой простирается довольно далеко. Она относится как к конкретным термодинамическим устройствам (типа тепловой машины), так и к общим законам термодинамики, каждому из которых нашелся свой эквивалент в физике черных дыр. Есть такой эквивалент и у известного термодинамического соотношения dE=θdS , где dE и dS – соответственно изменения энергии и энтропии тела; θ - температура2 . Если определить связь между изменением энергии черной дыры dE=d(Mc²) и изменением ее поверхности dF=8πRg dRg , то, оказывается, она имеет вид dE=(c²/8πG)gdF , где g=c4 /4GM – ускорение свободного падения на поверхности черной дыры.
Сопоставляя приведенные выражения для dE в термодинамике и физике черных дыр, можно прийти к следующему выводу: так как есть аналогия между поверхностью черной дыры F и энтропией S , то имеется и аналогия ускорения свободного падения на поверхности черной дыры g с температурой θ .
ТЕМПЕРАТУРА И ЭНТРОПИЯ ЧЕРНОЙ ДЫРЫ.
Существование черной дыры само по себе парадоксально. Черная дыра ведет себя, как тело с температурой, равной абсолютному нулю, потому что с помощью черной дыры можно полностью превратить тепло в работу.
При падении на черную дыру тело может производить работу за счет энергии гравитационного притяжения к черной дыре. Если какое-либо тело падает на черную дыру, то вся его энергия вместе с «энергией покоя» M0 c² (M0 - масса покоя тела) может быть превращена в работу1 .
Таким образом, на границе черной дыры полная энергия тела обратится в нуль. Можно сказать, что масса покоя тела погасится отрицательной потенциальной энергией тела в гравитационном поле черной дыры. В обычных земных условиях потенциальная энергия очень мала по сравнению с энергией покоя, так что масса падающего камня остается практически неизменной; при падении в поле черной дыры она обращается в нуль.
Закон тяготения действует так, что сила притяжения пропорциональна массе притягиваемого тела независимо от того, с чем связана эта масса. Горячий чайник немного тяжелее холодного; падая на черную дыру, горячий чайник выделит несколько больше энергии (на U/c² , где U – внутренняя энергия), чем холодный. Черная дыра работает как идеальный холодильник при Т=0, из которого никакими способами нельзя извлечь какой-либо энергии. Это значит, что к.п.д. цикла с черной дырой в качестве холодильника, по Карно, будет равен единице. Возникает ситуация, очень напоминающая вечный двигатель второго рода, и нарушается теорема Нернста. Такой парадокс должен был неминуемо навести на мысль, что черная дыра не может иметь температуру Т=0.
Решение парадокса надо было искать в термодинамических свойствах черной дыры. Первая догадка состояла в следующем.
Если черная дыра имеет температуру, отличную от абсолютного нуля, то она имеет и энтропию. Если черная дыра сферически симметрична, не вращается и не заряжена, то энтропия может зависеть только от массы. Но энтропия – величина, которая не зависит от единиц измерения: энтропия идеального газа определялась отношением объемов и отношением температур. Численное же значение массы, конечно, зависит от того, в каких единицах мы ее измеряем – в граммах или в миллионах тонн. По-видимому, и энтропия черной дыры должна определяться отношением ее массы к какой-то стандартной эталонной массе. Но какой? Как все же должно выглядеть выражение для энтропии черной дыры?
Качественное решение задачи было придумано Бекенштейном. Внимание его привлекла одна теорема общей теории относительности. Теорема утверждала, что какие бы процессы ни происходили в системе, в которой есть черные дыры, суммарная площадь поверхностей черных дыр может только увеличиваться. Эта очень общая теорема похожа на теорему о возрастании энтропии. Площадь, так же как энтропия, величина аддитивная и, так же как и энтропия, зависит от массы черной дыры. Поэтому был соблазн предположить, что энтропия черной дыры просто пропорциональна ее площади: S~A . Но как свести концы с концами, если площадь A имеет размерность квадрата длины?
В микромире нет своего масштаба длины. Из двух постоянных ћ и c нельзя составить величинусразмерностью длины или времени. Для этого надо взять еще массу. Тогда длину можно, например, составить так: ћ/mc .
В общей теории относительности также нет масштаба длины, так как его нельзя составить из G и c . Но если привлечь на помощь массу, то длину можно составить так: Gm/c² .
Объединим теперь обе длины ћ/mc и Gm/c² , составив их геометрическое среднее (ћG/c³)½ . При этом масса сократится. Это и есть единица длины, предложенная Планком.
После того как Планк ввел две фундаментальные постоянные ћ и k , он заметил, что появилась возможность построить новую систему единиц, не связанную ни с какими искусственными эталонами. Это следующие единицы: длина lп =(ћG/c³)½ =5,110*10-31 м,
Время tп =(ћG/c5 )½ =1,7016 *10-43 с,
Масса mп =(ћc5 /G)½ =6,189*10-9 кг,
Температура Тп =1/k(ћc5 /G)½ = 4,028*1031 К.
Единицы Планка удобны при расчете таких систем, где существенны эффекты как квантовые, так и гравитационные.
Черная дыра (и ее энтропия) кажется удачным кандидатом для применения единиц Планка.
Предположим, что масштаб энтропии связан с постоянной длины lп , т.е. что площадь поверхности черной дыры надо разделить на lп 2 с каким-то коэффициентом, о котором, конечно, нельзя догадаться заранее. На основе таких не очень строгих рассуждений и была выдвинута гипотеза о том, что энтропия черной дыры должна иметь вид S=αΑ/ lп 2 , где коэффициент α надо вычислить из каких-то соображений особо. Такая догадка оказалась правильной. Коэффициент α был вычислен позднее Хокингом. Он оказался равным 1/4.
Зная энтропию, можно вычислить и температуру. Заменим площадь A ее выражением через гравитационный радиус:
A=4πRg ²=16πGM²/c4 .
Используя единицы Планка, можно теперь написать формулу для энтропии:
S=16πα(M/mп )² .
Температура запишется в виде
T=1/(32πα)* mп /M*Tп .
Исключая из этих формул массу, будем иметь (в единицах Планка и α=1/4) ST²=1/(16π).
Такое уравнение состояния ни на что не похоже. Из него следует, что чем выше температура, тем меньше энтропия, а при абсолютном нуле энтропия обращается в бесконечность.
Отсюда можно заключить, что либо в наших рассуждениях грубая ошибка, либо с черно дырой происходит нечто серьезное и она не «доживает» до абсолютного нуля. Но в рамках классических представлений парадокс разрешить оказалось невозможным.
Парадокс исчез, когда Хокинг теоретически доказал, что вблизи черной дыры происходит рождение частиц. Неожиданным образом выяснилось, что теорема о возрастании площади поверхности черной дыры перестает быть строгой в квантовой механике и энтропия ее может уменьшаться за счет того, что вокруг нее создается поток фотонов, которые эту энтропию уносят.
Очень большой потенциал гравитационного поля вблизи черной дыры приводит к тому, что на ее поверхности рождаются пары фотонов (и другие частицы). Энергия этих фотонов (как и всех частиц вблизи черной дыры) равна нулю, поэтому они могут родиться «из ничего», не нарушая закона сохранения энергии. После рождения пары фотонов один из них уходит в черную дыру1 , а второй за счет освободившейся энергии улетает на бесконечность. Система работает, как блок: один груз опускается, а за его счет поднимается другой. Результатом этого процесса будет уменьшение массы черной дыры (а значит, и ее поверхности), эквивалентное энергии улетевших фотонов.
Теория этого процесса сложна. Но результат был интересным. Черная дыра излучает фотоны, спектр которых совпадает с распределением Планка, отвечающим температуре (в единицах Планка, т.е. mп =1 и Tп =1 ):
T=1/(8π)*1/М.
Из этой формулы следует, что коэффициент α=1/4.
Таким образом, черная дыра излучает как идеальное черное тело (неожиданно реализованное в космосе с очень большой точностью).
Теперь становится ясным источник парадокса. Черная дыра – система неустойчивая, неравновесная, поэтому и понятие о температуре черной дыры - понятие не вполне точное. Температура черной дыры растет с уменьшением массы; рождение пар приводит к уменьшению массы, а, следовательно, и к повышению температуры. С ростом температуры интенсивность излучения увеличивается, а температура возрастает еще больше. В конце концов, черная дыра должна сгореть совсем, причем сгореть за конечное время.
ТЕРМОДИНАМИКА И ИНФОРМАЦИЯ.
ИНФОРМАЦИООНЫЙ ПОДХОД К ТЕРМОДИНАМИКЕ.
Мы уже видели, насколько важно для возникновения тепловых свойств черной дыры существование горизонта событий, отделяющего область пространства, информация о которой не доходит до внешнего наблюдателя. Было показано, как можно прийти к эффекту Хокинга и термодинамике черных дыр с помощью простых термодинамических соображений, без проведения динамических расчетов рождения пар в поле черной дыры. Оказывается возможным сделать и следующий шаг - связать тепловые свойства черной дыры прямо с самим фактом существования у нее горизонта событий.
Эта возможность основана на информационном подходе к термодинамике, который восходит к классикам теории теплоты, был сформулирован Л. Сциллардом и развивался многими физиками и математиками. Суть этого подхода состоит в утверждении, что существует прямая связь между недостатком информации о физической системе и величиной ее энтропии.
Будучи приложен к физике черных дыр, информационный подход прямо указывает на существование у них отличной от нуля энтропии и температуры, позволяя осуществить непосредственный переход от утверждения «внешний наблюдатель лишен информации о внутренней части черной дыры» к утверждению «такой наблюдатель увидит черную дыру как горячее тело».
С другой стороны, физика черных дыр подкрепила информационный подход, подтвердив, что недостаток информации о системе, с чем бы он ни был связан, действительно проявляется в возникновении у нее тепловых свойств. Сегодня, после открытия эффекта Хокинга и других эффектов такого же рода, нам известно уже несколько механизмов потери информации и соответственно несколько механизмов появления тепловых свойств у динамической системы.
ЭНТРОПИЯ И ИНФОРМАЦИЯ.
Прежде чем давать количественную формулировку информационного подхода к термодинамике, напомним обычную картину перехода динамической системы в состояние термодинамического равновесия. В процессе такого перехода система быстро « забывает » свое начальное состояние, что происходит вследствие « запутывания » (стохастизации) движения составляющих ее частиц. Это вызывается динамическими неустойчивостями в системе, которые ведут к усилению неизбежно присутствующих малых неопределенностей начальных значений динамических переменных. В результате возникает быстрое перемешивание состояний частиц и равномерное заполнение всей доступной этой системе области значений динамических переменных.
Такое состояние системы, отвечающее равновероятности всех возможных микроскопических состояний составляющих ее частиц, описывается так называемым микроканоническим распределением. Из него автоматически следует, что любая достаточно большая часть системы описывается формулой Гиббса.
Поскольку равновесная система «забывает» свое начальное состояние, она характеризуется существенно меньшим числом параметров (энергией или температурой, давлением или объемом и т.п.), чем полное число ее степеней свободы. Поэтому состояние термодинамического равновесия вырождено: каждому набору только что перечисленных макроскопических параметров отвечает огромное число N различных микросостояний системы, реализующих этот набор. Мерой этого вырождения и служит энтропия системы S = k ln N .
Равновероятность различных микросостояний термодинамически равновесной системы означает, что никакое из них нельзя предпочесть другому. Поэтому чем больше величина N , тем меньшим объемом сведений о микроструктуре системы мы располагаем, и энтропию можно считать мерой неполноты информации об истинной микроскопической структуре равновесной системы.
Мы подошли, таким образом, к информационному определению энтропии. Чтобы дать его точную формулировку, нужно ввести следующее простейшее определение изменения количества информации ∆І при некотором процессе. Если сначала имелось P равновероятных ответов на вопрос, касающийся какого-либо предмета или явления, а в конце их число стало p , то изменение информации об этом предмете или явлении есть
∆І= k ln ( P / p ).
ЕслиP > p , мы имеем дело с приростом информации (наши сведения стали более определенными), в обратном случае – с ее убылью.
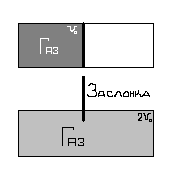 Применим сказанное к процессу перехода динамической системы в состояние термодинамического равновесия (рис.2).
Применим сказанное к процессу перехода динамической системы в состояние термодинамического равновесия (рис.2).
Рис. 2. Пример, иллюстрирующий справедливость соотношения ∆І=–∆ S – необратимое расширение газа в пустоту.
Первоначально газ занимает левую половину устройства – объем v0 (вверху). После поднятия заслонки газ расширяется, заполняя вдвое больший объем. В результате неопределенность в положении молекул газа (и число ответов на соответствующий вопрос) также увеличивается вдвое: P/p=1/2. Соответственно убыль информации о положении молекул будет определяться соотношением ∆I=–kln 2. Из термодинамики известно, что прирост энтропии (на одну молекулу) при таком процессе есть ∆S=kln 2, что точно соответствует равенству ∆S=-∆I.
Вначале система была чисто динамической, ее энтропия равнялась нулю, и мы точно знали ответ на вопрос о ее микросостоянии: P=1. В конце ее энтропия увеличилась на ∆ S , а число ответов на указанный вопрос выросло до значения N .Поэтому ∆I =- k ln N , и мы приходим к важному соотношению:∆ S = - ∆I .
Уменьшение количества информации о физической системе соответствует увеличению ее энтропии1 . Более того, если эта потеря информации такова, что отражает равновероятность всех допустимых микросостояний, то наша система описывается микроканоническим распределением, а ее подсистемы – формулой Гиббса. Поскольку в приведенных рассуждениях никак не фигурировал конкретный механизм потери информации, сказанное в равной степени относится и к обычному горячему телу, и к черной дыре. Можно добавить, что наши утверждения не противоречат обычному представлению о том, что тепло отвечает хаотическому состоянию вещества. Ведь хаос в самом широком смысле – это и есть равновероятность различных микросостояний, когда ни одно из них нельзя предпочесть другому. Одновременно это и отсутствие информации о внутренней структуре системы.
Важно подчеркнуть, что, говоря о неполноте и потере информации, мы имели в виду, конечно, объективную невозможность получить информацию о состоянии системы – невозможность, характерихующую саму систему, а не субъекта-наблюдателя. Последний мог бы просто отказаться от получения полной информации, не используя, например, всех возможностей измерительной техники. Разумеется, к такой ситуации сказанное выше ни в малейшей мере не относится. Достаточно вспомнить рассмотренный выше пример рождения пар в электрическом поле, когда отказ регистрировать позитронную компоненту излучения хотя и означает потерю информации, однако не приводит к термодинамической формуле Гиббса. В то же время рождение пар в поле тяготения, когда есть горизонт событий и потеря информации имеет объективный, неустранимый характер, ведет именно к этой формуле.
ЧЕРНЫЕ ДЫРЫ И ВРЕМЯ.
ЭФФЕКТ ЗАМЕДЛЕНИЯ ВРЕМЕНИ НА ПОВЕРХНОСТИ ЧЕРНОЙ ДЫРЫ .
Плотное тело большой массы не только изменяет геометрические свойства пространства вокруг себя, но и влияет на темп течения времени и скорости, протекающих вблизи процессов.
Пусть ∆t– интервал времени между двумя событиями, которые происходят на расстоянии r от центра тела (r=Rтела), таким образом, события происходят на поверхности тела. Значит, t – собственное время, время, измеренное наблюдателем на поверхности тела.
Пусть ∆τ – промежуток времени между этими же событиями, который будет фиксировать наблюдатель, удаленный от этого тела «на бесконечность» (так называемое координатное время).
Из теории относительности следует, что оба эти интервала связаны между собой соотношением ([4],с.334):
∆τ= ∆t/√(1-Rg /r)= ∆t/√(1-2GM/rc2 )
Видно, что если r >> Rg , то ∆τ= ∆t – на больших расстояниях от гравитирующей массы координатное время совпадает с собствееным, т.е. где бы мы не находились на поверхности этого тела или много дальше от него время будет одно и то же. Но если r→ Rg , то при любом интервале собственного времени∆t имеем ∆τ→ ∞, то есть, если наблюдатель находится на большом расстоянии от черной дыры, то ему кажется, что время между событиями изменяется слишком медленно, а наблюдатель находящийся на поверхности черной дыры скажет, что время между событиями практически не заметно.
Под интервалом времени ∆t можно подразумевать и период электромагнитной волны T=1/ν=λ/c, таким образом λ=λ0 /√(1-Rg /r).
Отсюда следует, что длина волны λ, регистрируемая наблюдателем, будет больше длины волны λ0 , испускаемой атоиои на расстоянии r от центра конфигурации, и при r→ Rg , λ→ ∞.
Этот эффект замедления времени – эффект красного смещения длин волн вблизи гравитирующей массы (необходимо учитывать при изучении сжатия ядра звезды большой на конечном этапе эволюции).
После того, как поверхностные слои звезды пересекут сферу Шварцшильда, испускаемые ими лучи света уже не могут выйти к удаленному наблюдателю. Поэтому сфера Шварцшильда именуется еще горизонтом событий, а сжатие звезды за нее – гравитационным самозамыканием.
Представим себе, что наблюдатель «выгодно» устроился на верхнем слое сжимающегося ядра. Он фиксирует свое собственное время. Он обнаружил, что от начала движения с расстояния r =10Rg до r =Rg прошло несколько секунд. Скорость движения увеличилась до скорости света. Переход через поверхность сферы Шварцшильда для него длился мгновение.
Совершенно другую картину фиксирует наблюдатель, сидящий около телескопа в далекой галактике. Для него скорость движения верхнего слоя V сначала так же возрастает (при r =2Rg , V=½c!), потом движение замедляется, и при r →Rg уменьшается до нуля. Момент прохождения через поверхность сферы Шварцшильда, с точки зрения удаленного наблюдателя «отсрочен» в бесконечно далекое будущее.
КВАНТ ПРОСТРАНСТВА - ВРЕМЕНИ НА ПОВЕРХНОСТИ ЧЕРНОЙ ДЫРЫ.
Не зная никакой теории о черных дырах, так же можно получить формулу для кванта времени т пространства в сингулярности (ρ→∞). А получить это можно, используя метод размерностей.
Так как гравитация здесь очень велика, то квант времени в сингулярности (и пространства квант) зависит от G- гравитационной постоянной. А раз речь идет о том, что время и линейные размеры, которые являются качественными характеристиками в черных дырах, не являются постоянно текущими, а, наоборот, являются прерывными. То есть время квантуется, значит, квант времени зависит от постоянной Планка(ћ). И еще квант времени (τ) зависит от скорости света (c). То есть система параметров такова: τ, ћ, G, c.
Составим из этих параметров безразмерную комбинацию, с помощью которой найдем формулу для кванта времени.
τ*ћx *cy *Gz =1 ( 1)
Определимся с размерностями физических величин, входящих в выражение (1): [ћ]=Дж*с=Н*м*с=кг*м*с-2 *м*с=кг*м²*с-1 ; [c] = м* с-1 ; [G] =м³* с-2 кг-1 ; [τ]=с.
Подставим вместо параметров их единицы измерения в уравнение (1) и упростим его.
с*кгx *м2 x *с- x *мy *с- y *м3 z *с-2 z *кг- z =1.
с1- x - y -2 z *кг x - z *м 2 x + y +3 z =1.
Выражение (1) только тогда будет являться безразмерным, если показатели степеней будут равны нулю.
1-x-y-2z=0 x=-1/2Ά
x-z=0 => z=-1/2
2x+y+3z=0 y=2.5
Подставим в уравнение (1) значения x,y,z.
τ ћ-1/2 c5/2 G-1/2 =1
τ=√(ћG/c5 ) (2)
То есть мы получили, пользуясь теорией размерностей формулу для кванта времени, а зная его формулу можно получить формулу для кванта пространства в сингулярности (l=c* τ)
l=√(ћG/c3 ) (3)
Линейные характеристики так же являются не непрерывными величинами, т.е. квантуются. Таким образом, видно, что не зная сложной теории, можно достаточно просто получить качественные характеристики для черных дыр. Самое главное правильно определить систему параметров.
ТИПЫ ЧЕРНЫХ ДЫР.
До сих пор мы говорили о возникновении во Вселенной черных дыр звездного происхождения. Астрономы имеют все основания предполагать, что, помимо звездных черных дыр, есть еще другие дыры, имеющие совсем иную историю.
Из теории звездной эволюции известно, что черные дыры могут возникать на заключительных стадиях жизни звезды, когда она теряет устойчивость и испытывает неограниченное сжатие под действием сил тяготения. При этом масса звезды должна быть достаточно велика, иначе эволюция звезды может закончиться образованием либо белого карлика, либо нейтронной звезды. ([1].с.82)
Кроме черных дыр (обычных ), возникающих в конце звездной эволюции и имеющих такие же массы, как звезды, могут существовать и более массивные черные дыры, образующиеся, например, в результате сжатия больших масс газа в центре шаровых звездных скоплений, в ядрах галактик или в квазарах.
А могут ли существовать во Вселенной черные дыры, масса которых во много раз меньше массы обычных звезд?
Согласно современным космологическим представлениям Вселенная расширяется от сверхсжатого сингулярного состояния. Можно предполагать, что вещество во Вселенной в ходе ее расширения прошло все стадии от плотностей ~ 1093 г/см³ до сегодняшней средней плотности, не превосходящей 10 –29 г/см³. Значит, в далеком прошлом Вселенной, когда плотность вещества была чудовещно велика, имелись предпосылки для возникновения черных дыр сколь угодно малых масс. На возможность их возникновения впервые указали Я.Б. Зельдович и И.Д. Новиков еще в шестидесятых годах. Найти столь малые образования в огромных просторах космоса чрезвычайно трудно, и поэтому они еще не обнаружены. Сегодня разные способы поисков таких черных дыр, получивших название первичных ,- предмет многочисленных исследований и дискуссий.
В начале 60-х годов нашего века были открыты необыкновенные небесные тела – квазары.
В течении прошедших десятилетий выяснилось, что квазары – это необычно активные излучающие ядра больших галактик. Часто в них наблюдаются мощные движения газов. Сами звезды галактики вокруг таких ядер обычно не видны из-за огромного расстояния и сравнительно слабого их свечения по сравнению со свечением квазара. Выяснилось так же, что ядра многих галактик напоминают своего рода маленькие квазарчики и проявляют иногда бурную активность – выброс газа, изменение яркости и т.д., - хотя и не такую мощную, как настоящие квазары. Даже в ядрах совсем обычных галактик, включая нашу собственную, наблюдаются процессы, свидетельствующие о том, что и здесь “работает” маленькое подобие квазара.
То, что в центре галактики может возникнуть гигантская черная дыра, теперь кажется естественным. В самом деле, газ, находящийся в галактиках между звездами, постепенно под действием тяготения должен оседать к центру, формируя огромное газовое облако. Сжатие этого облака или его части должно привести к возникновению черной дыры. Кроме того, в центральных частях галактик находятся компактные звездные скопления, содержащие миллионы звезд. Звезды здесь могут разрушаться приливными силами при близких прхождениях около уже возникшей черной дыры, а газ этих разрушенных звезд, двигаясь около черной дыры, затем попадает в нее.
Падение газа в сверхмассивную черную дыру должно сопровождаться явлениями, подобными тем, о которых мы говорили в случае звездных черных дыр. Только здесь должно происходить ускорение заряженных частиц в переменных магнитных полях, которые приносятся к черной дыре вместе с падающим газом.
Все это вместе и приводит к явлению квазара и к активности галактических ядер.
ЗАКЛЮЧЕНИЕ.
Черные дыры – совершенно исключительные объекты, не похожие ни на что, известное до сих пор. Это не тела в обычном смысле слова и не излучение. Это дыры в пространстве и времени, возникающие из-за очень сильного искривления пространства и изменения характера течения времени в стремительно нарастающем гравитационном поле.
Черные дыры являются в некотором смысле и очень простыми объектами. Их свойства никак не зависят от свойств сколлапсировавшего вещества, от всех сложностей строения вещества, его атомной структуры, находящихся в нем физических полей, не зависят от того, было ли вещество водородом или железом и т.д. При образовании черной дыры для внешнего наблюдателя все свойства сколлапсировавшего тела как бы исчезают, они не влияют ни на границу черной дыры, ни на что другое во внешнем пространстве, остается только гравитационное поле, характеризуемое лишь двумя параметрами – массой и вращением. Этим определяются и форма черной дыры, и ее размеры, и все остальные ее свойства. Так что с полной определенностью можно сказать, что нет ничего проще черной дыры.
Но и нет ничего более сложного, чем черная дыра, - ведь человеческое воображение даже не в состоянии представить себе, до какой степени происходит искривленин пространства и изменение течения времени, что в них возникает дыра.
СПИСОК ЛИТЕРАТУРЫ.
1. Прошлое и будущее Вселенной. Под ред. А.М. Черепащук, М., Наука, 1986г.
2. И.Новиков . Черные дыры и Вселенная. М., “Молодая гвардия”, 1985г.
3. Дж.Нарликар. От черных облаков к черным дырам. М., Энергоатомиздат, 1989г.
4. И.А.Климишин . Астрономия наших дней. М., Наука,1986г.
5. И.Николсон. Тяготение, черные дыры и Вселенная. М., Мир ,1983г.
6. Я.А. Смородинский. Температура. М., Наука, 1987г.
7. Энциклопедический словарь по физике.
8. Энциклопедический словарь юного астронома.
1 К этому выводу можно прийти, если воспользоваться законом сохранения энергии в классической механике; энергия световой корпускулы массы m на поверхности тела массы M , равная mc²/2- GmM/ Rg , должна быть меньше нуля (ее минимальной энергии на бесконечнрсти).
1 Поэтому само название «черная дыра», введенное еще до открытия эффекта Хокинга, потеряло свой первоначальный смысл.
2 Физический вакуум (современный аналог понятия пустоты) – состояние, в котором отсутствуют реальные частицы.
3 Горизонт событий – это поверхность сферы гравитационного радиуса
1 Это справедливо только в неквантовой теории тяготения: эффект Хокинга ведет к уменьшению поверхности, сопровождающемуся ростом энтропии, связанной с излучением.
2 Для простоты выписана лишь тепловая составляющая dE. Слагаемое, отвечающее работе, имеет для вращающегося заряженного тела вид ΩdJ+φdQ, где Ω – угловая скорость; φ – электрический потенциал. Точно такое же слагаемое возникает в выражении для изменения энергии вращающейся заряженной черной дыры.
1 Эта работа реализуется в виде мощного излучения электромагнитных и гравитационных волн.
1 Можно говорить, что фотоны, проваливаясь в черную дыру, приобретают отрицательную (потенциальную) энергию.
1 Отметим, что может иметь место и обратная ситуация, когда приобретение дополнительной информации о внутреннем состоянии системы может быть использовано для уменьшения ее энтропии, т.е. для частичного ее упорядочения. Именно на этом основана наука об управлении. Соответствующие технические устройства – регуляторы – обязательно имеют специальный орган для извлечения информации о регулируемой системе.

