ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ, СТАТИСТИКИ И ИНФОРМАТИКИ
ИНСТИТУТ СТАТИСТИКИ И ЭКОНОМЕТРИКИ
КАФЕДРА МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
И ЭКОНОМЕТРИКИ
Лабораторная работа№1
ИССЛЕДОВАНИЕ РИСКА
В АВТОТРАНСПОРТНОМ СТРАХОВАНИИ
Работу выполнила
студентка группы ДЭС-401
Чумарина Д.Р.
Вариант №19
МОСКВА 2008
Задание:
Подготовить массив исходных данных согласно своему варианту. (см. выше)
2. Проанализировать распределение числа убытков в одном договоре на соответствие двум законам распределения:
- Пуассоновскому ;
- отрицательному биномиальному.
3. Исследовать распределение величины ущерба при наступлении одного страхового случая и подобрать наиболее подходящее распределение, смоделировав:
- нормальным,
- логнормальным,
- экспоненциальным,
- гамма – распределением.
4. Сделать выводы.
I.Исследование распределения числа страховых случаев в одном договоре
Подготовим исходный массив данных, для этого рассчитаем С, исходя из номера варианта (№19).
C=200+k*10,
Следовательно, C=200+19*10=390
Подготовив исходный массив данных, отберем договора без убытка, с одним убытком, двумя убытками и т.д. Результаты отбора запишем в Таблицу 1.
Таблица 1
| i | mi |
| 0 | 5242 |
| 1 | 123 |
| 2 | 1 |
| N | 5366 |
Далее приступим к анализу числа убытков в одном договоре.
При анализе распределения количества урегулированных убытков необходимо проверить возможность аппроксимации ряда законом Пуассона и отрицательным - биномиальным. Для отдельного клиента имеет место биномиальный закон распределения, поэтому для однородного портфеля общее число случаев за срок действия договора подчиняется закону Пуассона (формула Пуассона аппроксимирует формулу Бернулли). При определенных условиях оба закона распределения можно аппроксимировать нормальным законом. Данное обстоятельство объясняет причину широкого применения указанных распределений в актуарных расчетах.
Распределение Пуассона
Распределением Пуассона называется такое распределение дискретной случайной величины, при котором она может принять одно из возможных значений 0,1,2……..,n с вероятностью :
 ,
,
где m=0,1,2,……,n;
=np-параметр распределения, характеризующий интенсивность появления событий в n испытаниях.
Распределение Пуассона может быть задано в виде ряда распределения, значения которого определяется и в виде функции распределения:
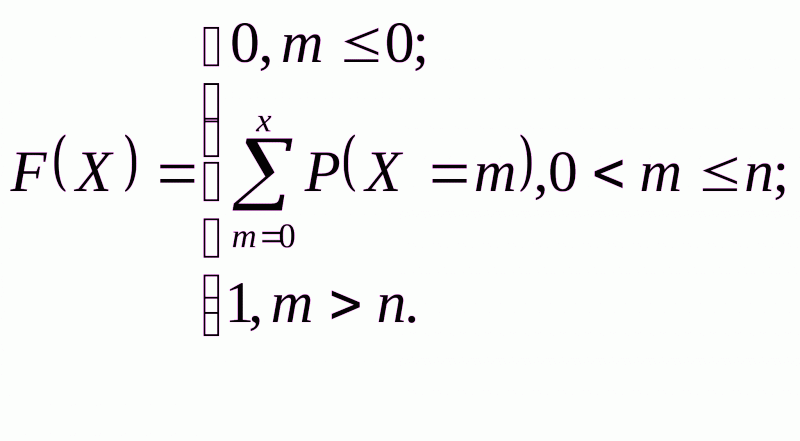
 Числовые характеристики распределения Пуассона:
Числовые характеристики распределения Пуассона:

Распределение Пуассона является предельным случаем биномиального распределения при  Отсюда следует, что распределение Пуассона с параметром =np можно применять вместо биномиального, когда число опытов n достаточно велико, а вероятность p- достаточно мала, т.е. в каждом отдельном опыте интересующее событие происходит крайне редко.
Отсюда следует, что распределение Пуассона с параметром =np можно применять вместо биномиального, когда число опытов n достаточно велико, а вероятность p- достаточно мала, т.е. в каждом отдельном опыте интересующее событие происходит крайне редко.
Статистическая оценка параметра распределения Пуассона находится по формуле:
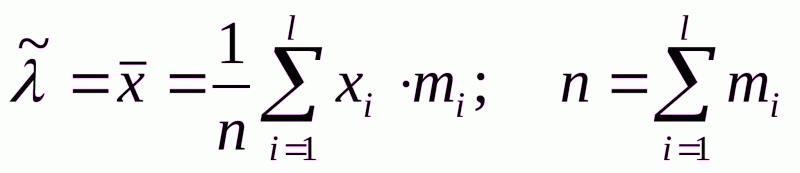 .
.
Для анализа количества страховых случаев в одном договоре необходимо найти статистические оценки параметров распределения. Запишем их в Таблицу 2.
Таблица 2
| i | mi | M(x) | M(x2) | D(x) | p | mрасч1 | 2набл | 2крит |
| 0 | 5242 | 0,022922 | 0,023668 | 0,022362 | 0,9773 | 5244 | 0,001097 | 3,841459 |
| 1 | 123 | 0,0224 | 120 | |||||
| 2 | 1 | 0,0003 | 1 | |||||
| N | 5366 | 1,0000 | 5366 |
Оценка параметра Пуассоновского распределения λ равна математическому ожиданию. И видно, что значения М(Х) и D(X) очень близки, что говорит о возможной применимости в этом случае Пуассоновского распределения.
Теоретические частоты mрасч, найденные для распределения Пуассона с заданным параметром λ=М(Х), находятся умножением полученных вероятностей Pn(i) на общее число страховых случаев N=5366.
Теперь с помощью критерия согласия 2 проверим гипотезу об адекватности пуассоновской модели. Для этого рассчитаем 2набл (См. Таблицу 2).
2крит при =0,05 и числе степеней свободы ν=k-r-1=3-1-1=1 (k – число интервалов, r – число параметров теоретического распределения, здесь r=1, это λ) можно найти с помощью функции ХИ2ОБР, 2крит=3,841459.
Для рассматриваемого примера 2набл= 2крит при =0,05 , т.е. гипотеза не отвергается, следовательно, пуассоновская модель признается адекватной для распределения урегулированных убытков в группе ГО.
Отрицательное биномиальное распределение
Теперь необходимо проверить возможность аппроксимации урегулированных убытков отрицательным биномиальным законом.
Случайная величина Х имеет отрицательное биномиальное распределение с параметрами (r,p), если в последовательности испытаний Бернулли с вероятностью успеха р и вероятностью неудачи q=1-p вероятность числа неудач k, происшедших до a-го успеха, определяется по формуле:
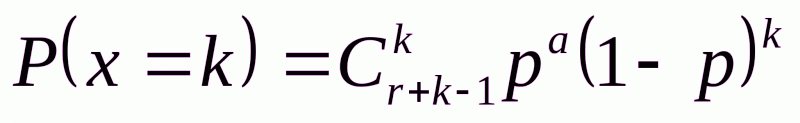 ,
,
где r - число успехов, целое положительное число;
k - число неудач, происшедших до числа успехов a.
Числовые характеристики отрицательного биномиального распределения:
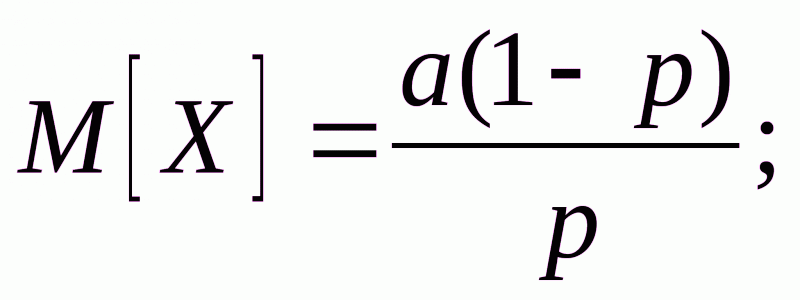
 ,
,
из формул (2) получили формулы для оценки параметров p и a:
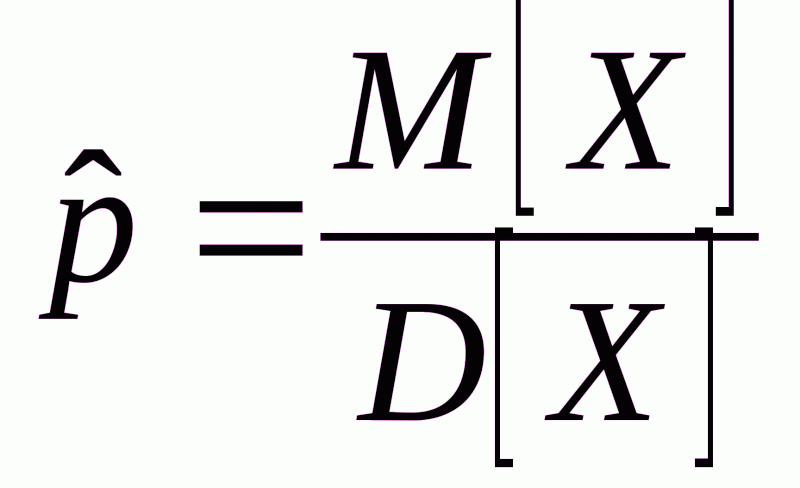 ;
; 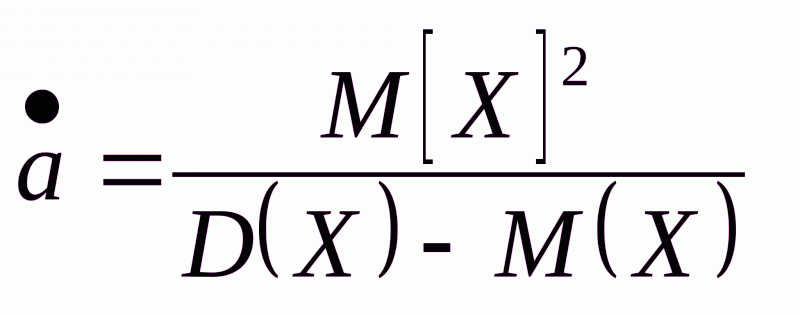 .
.
Очевидно, что это распределение применимо, только если математическое ожидание изучаемой случайной величины не превышает дисперсии, иначе вероятность получается больше 1.
После подсчета М(Х) и D(X) рассчитаем оценки параметров для отрицательного биномиального распределения по формулам приведенным выше. Результаты запишем в Таблицу 3.
Таблица 3
| i | mi | M(x) | M(x2) | D(x) | p | a | Pn(mi) |
| 0 | 5242 | 0,022922 | 0,023668 | 0,022362 | 1,0250 | 0,938 | #ЧИСЛО! |
| 1 | 123 | ||||||
| 2 | 1 | ||||||
| N | 5366 |
Видно, что т.к. математическое ожидание изучаемой случайной величины превышает дисперсию, вероятность получилась больше 1, значит, применение отрицательного биномиального распределения невозможно.
Это можно проверить, если применить функцию ОТРБИНОМРАСП.
В результате примения данной функции, получилось, что вероятность_успеха > 1 и число_успехов < 1, следовательно, функция возвращает значение ошибки #ЧИСЛО! Отрицательное биномиальное распределение в этом примере не приемлемо.
II. Исследование распределения величины ущерба
при наступлении одного страхового случая
Для дальнейшей обработки данных необходимо отобрать все урегулированные убытки, произошедшие в 2003 году. Для этого надо воспользуемся командой фильтр, и в столбце «Сумма фактически выплаченного возмещения» поставить условие «не равно 0». После отбора всех сумм фактически выплаченного возмещения в 2003 году, необходимо скопировать этот столбец в ППП Statistica 6.0.
Рассмотрим анализ величины ущерба в группе ГО в 2003 году. Для этого необходимо проверить возможность аппроксимации данной величины непрерывными законами распределения: нормальным, логнормальным, экспоненциальным и гамма - распределением.
2.1. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону)(1), если плотность распределения вероятности f(x) имеет вид:

где а и s—некоторые постоянные, называемые параметрами нормального распределения.
Функция распределения F(x) в рассматриваемом случае принимает вид:

Параметр а- есть математическое ожидание случайной величины, имеющей нормальное распределение, s - среднее квадратическое отклонение, тогда дисперсия равна:

Выберем в окне пункт «Continuous distributions» (Непрерывные распределения), что означает выбор непрерывного распределения, и необходимое распределение: «Normal». Результаты проверки на нормальное распределение приведены в Таблице 4 и на Графике 1.
Таблица 4

По полученным результатам можно сделать вывод о том, что эмпирические частоты не совпадают с полученными теоретическими. Рассмотрим График 1.

График 1. Проверка на нормальное распределение
При рассмотрении Графика 1 приходим к этому же выводу.
Сравним также эмпирические данные с полученными теоретическими с помощью критерия Колмогорова-Смирнова и критерия 2.
Критерий Колмогорова-Смирнова тест 
С помощью критерия Колмогорова-Смирнова необходимо проверить гипотезу о том, что величина размера ущерба распределена по нормальному закону. Для этого необходимо сравнить dнабл. и dкрит при заданном уровне , а затем принять или отвергнуть гипотезу.
dкрит находится по таблицам распределения Колмогорова-Смирнова, а при большом числе договоров (n>100) по асимптотическим формулам:

где k1-α - квантиль порядка 1-α распределения Колмогорова, которые находят по таблице:
Асимптотические критические значения k1-α для статистик Колмогорова и Смирнова-Колмогорова
| α | 0,2 | 0,1 | 0,05 | 0,02 | 0,01 |
| k1-α | 1,073 | 1,224 | 1,358 | 1,517 | 1,628 |
Кроме того, расчёт dкрит возможен при n→∞ по асимптотическому соотношению:
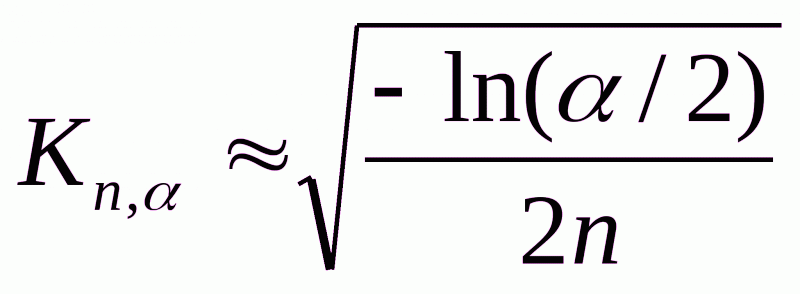
В рассматриваемом примере n=125, =0.05, расчёты по приведённым асимптотическим формулам приводят к dкрит= 0,121463 по 1-й формуле и dкрит= 0,121463 по 2-й формуле.
dнабл=0,23, и dнабл>dкрит=0,115 при =0,05, т.е. гипотеза о нормальном законе распределения отвергается.
Далее необходимо аналогично проверить возможность аппроксимации других распределений – логнормального, экспоненциального и гамма-распределения.
dнабл=0,23 , и dнабл>dкрит=0,121 при =0,05, т.е. гипотеза о нормальном законе распределения отвергается.
Далее необходимо аналогично проверить возможность аппроксимации других распределений – логнормального, экспоненциального и гамма-распределения.
2.2. ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Осуществим проверку на логнормальное распределение. Случайная величина X имеет логарифмическое нормальное (логнормальное) распределение (1) с параметрами a и σ, если случайная величина ln x имеет нормальное распределение с параметрами a> 0 и σ . Функция плотности вероятностей p (x), функция распределения F (x) и моменты M(X) , D(X) логнормального распределения имеют, соответственно, вид:
 ;
;  ,
,  .
.
Таблица 5


График 2. Проверка на логнормальное распределение
Сравним эмпирические данные с полученными теоретическими с помощью критерия Колмогорова-Смирнова и критерия 2. Kolmogorov-Smirnov d = 0,05471
dнабл<dкрит=0,121 при =0,05, т.е. гипотеза о том, что данная совокупность распределена по логнормальному закону, не отвергается. Следовательно, для этого примера можно считать адекватным логнормальное распределение.
2.3. ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Осуществим проверку на экспоненциальное распределение.
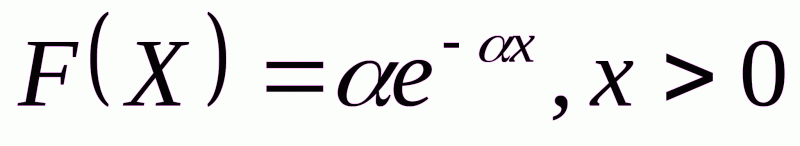 ;
;  ,
,  .
.
Таблица 6

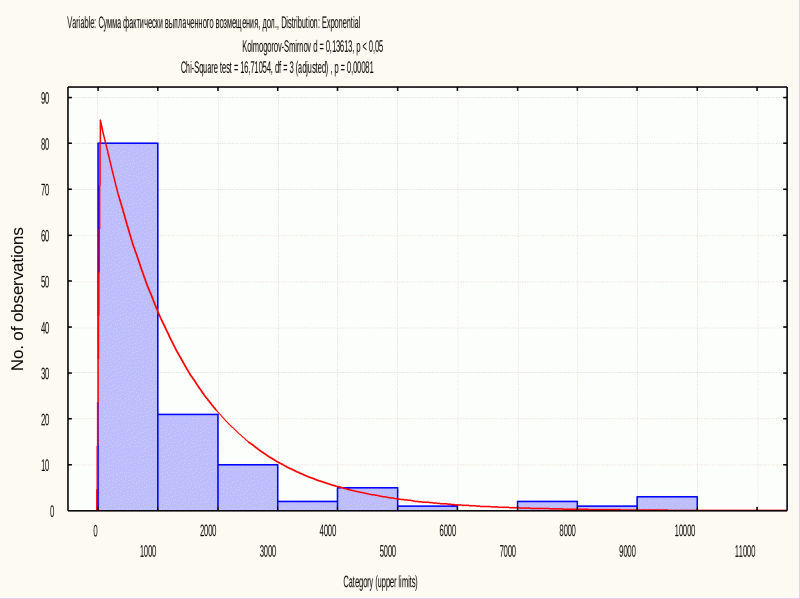 График 3. Проверка на экспоненциальное распределение
График 3. Проверка на экспоненциальное распределение
Сравним эмпирические данные с полученными теоретическими с помощью критерия Колмогорова-Смирнова и критерия 2. Kolmogorov-Smirnov d = 0,13613, p < 0,05
dнабл>dкрит=0,121 при =0,05, т.е. гипотеза о том, что данная совокупность распределена по экспоненциальному закону, отвергается.
2.4. ГАММА РАСПРЕДЕЛЕНИЕ
Осуществим проверку на гамма распределение.
 ,
,  ,
,  .
.
Таблица 7


График 4. Проверка на гамма распределение
Сравним эмпирические данные с полученными теоретическими с помощью критерия Колмогорова-Смирнова и критерия 2. Kolmogorov-Smirnov d = 0,13633, p < 0,05
dнабл>dкрит=0,121 при =0,05, т.е. гипотеза о том, что данная совокупность распределена по закону гамма распределения, отвергается.
Выводы.
1. Проанализировав распределение числа убытков в одном договоре на соответствие двум законам распределения, Пуассоновскому и отрицательному биномиальному, было определено на основе 2, что для рассматриваемого примера адекватной признается пуассоновская модель.
Отрицательное биномиальное распределение в этом примере не приемлемо т.к. математическое ожидание изучаемой случайной величины превышает дисперсию, а также вероятность_успеха > 1 и число_успехов < 1.
2. Исследуя распределение величины ущерба при наступлении одного страхового случая, было определено на основе анализа теоретических и эмпирических частот, а также критерия Колмогорова-Смирнова, что гипотеза о том, что данная совокупность распределена по логнормальному закону, не отвергается. Следовательно, для этого примера можно считать адекватным логнормальное распределение.
Согласованность эмпирических и теоретических частот, рассчитанных с помощью логнормального распределения, изобразим на Графике 5.

График. 5. Согласованность эмпирических и теоретических частот, рассчитанных с помощью логнормального распределения
График 5 подтверждает справедливость того, что данная совокупность подчинена логнормальному распределению.

