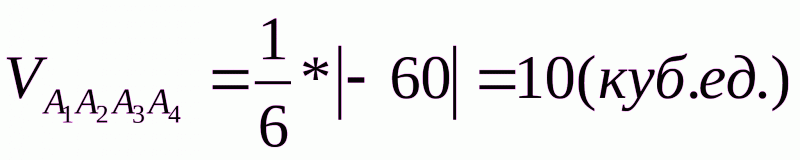Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Контрольная работа По дисциплине: Алгебра и геометрия
Выполнил: Шевыряев А.Н.
Группа: СДТ-03
Вариант:6
Проверил: ___________________
Новосибирск, 2010 г
Задача 1. Дана система трех линейных уравнений. Найти решение ее двумя способами: методом Крамера и методом Гаусса.
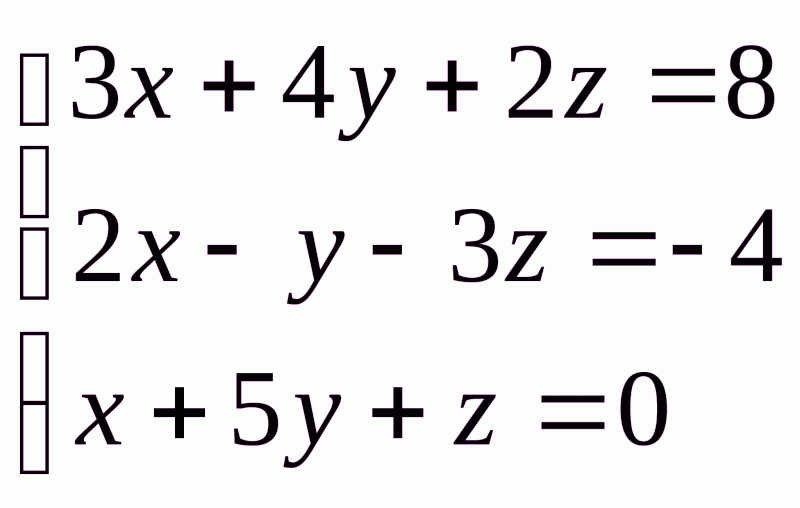
Решение системы методом Крамера.
Формулы Крамера:
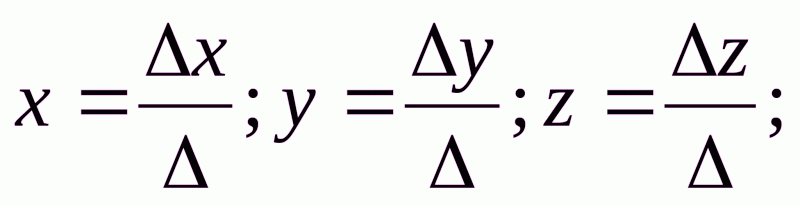
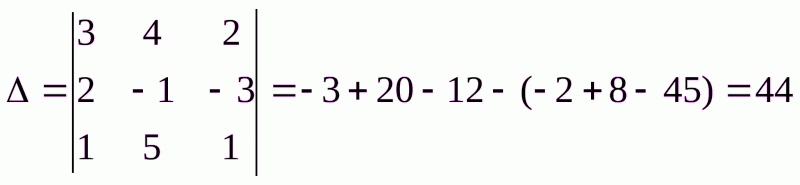
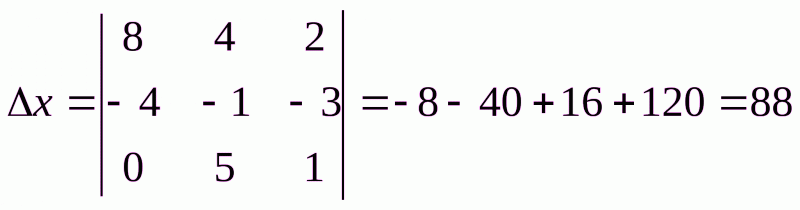
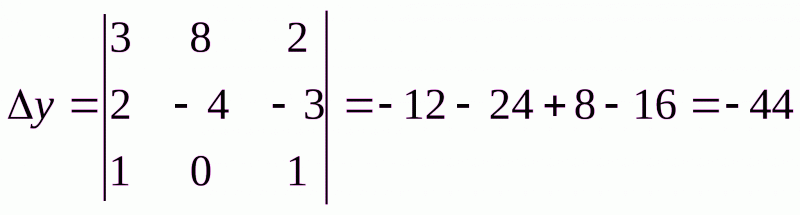
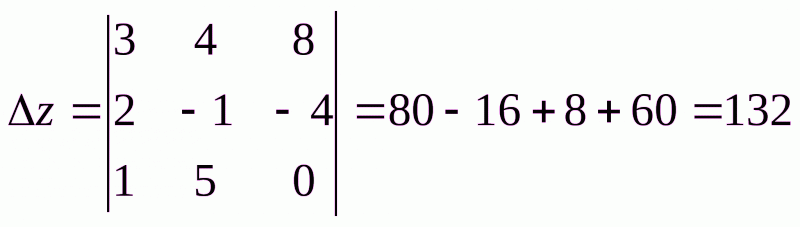
Найдем значения неизвестных:
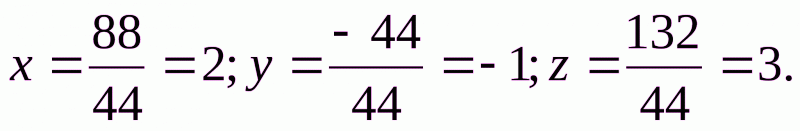
Выполним проверку:
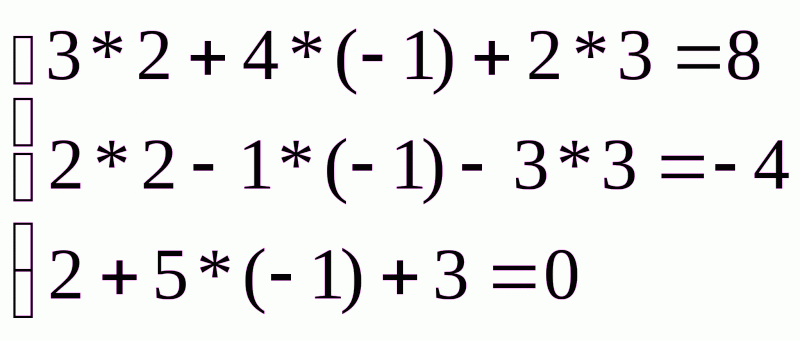
Решение системы методом Гаусса.
Составим расширенную матрицу системы:

Выполним преобразования:
умножим первую строку на (-2) и сложим со 2-й строкой матрицы;
умножим первую строку на (-3) и сложим с 3-й строкой матрицы;
умножим 2-ю строку на (-1) и сложим с 3-й строкой матрицы.
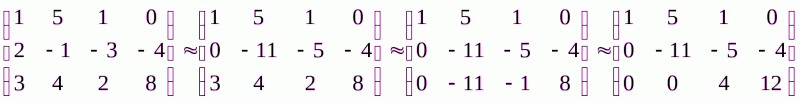
В результате получили матрицу системы треугольного вида.
Запишем итоговую систему:
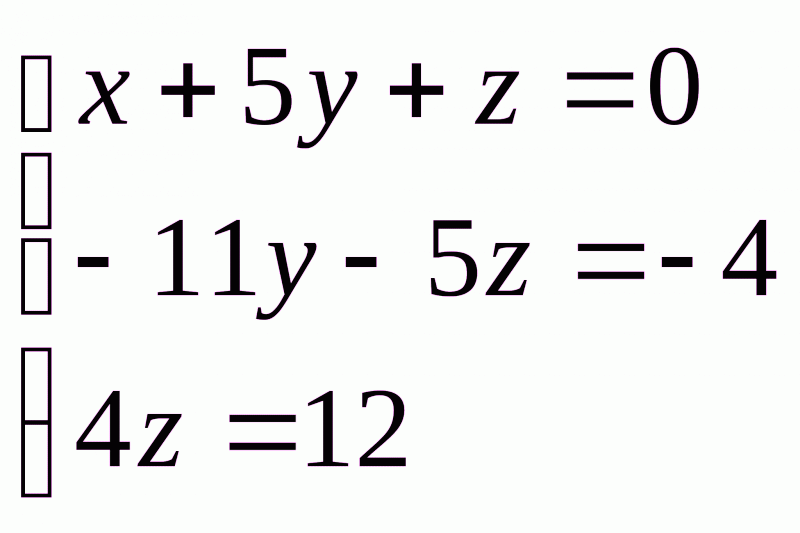
Найдем значения неизвестных: 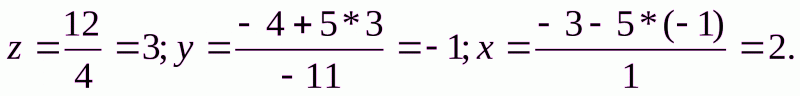
Задача 2. Даны координаты вершин пирамиды  . Найти:
. Найти:
длину ребра  ;
;
угол между ребрами  и
и 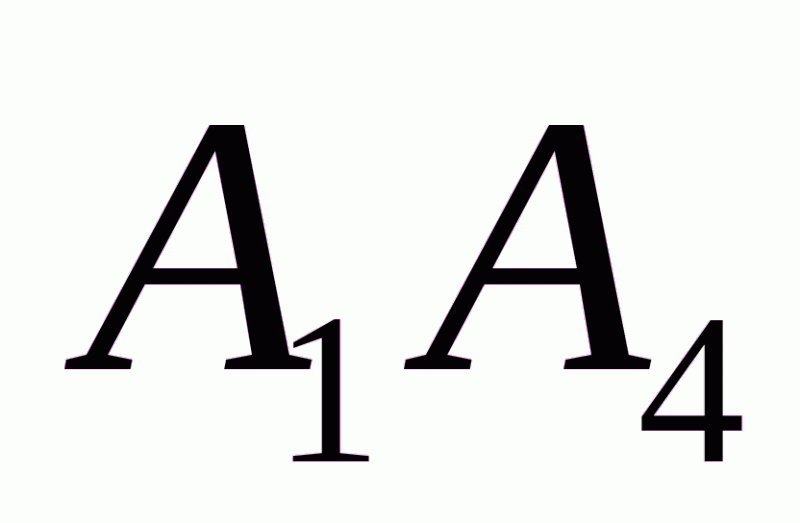 ;
;
площадь грани 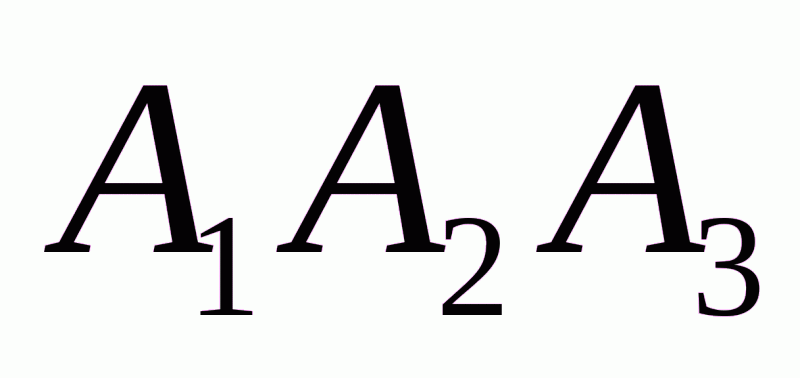 ;
;
уравнение плоскости 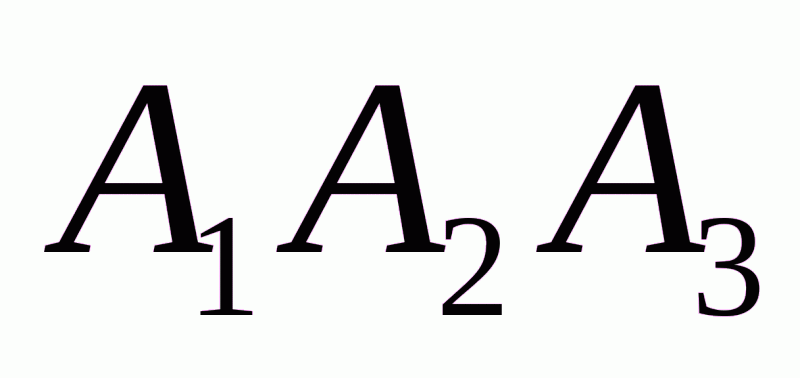 .
.
объём пирамиды  .
.
Решение.
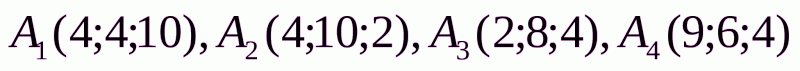
Рисунок 1.
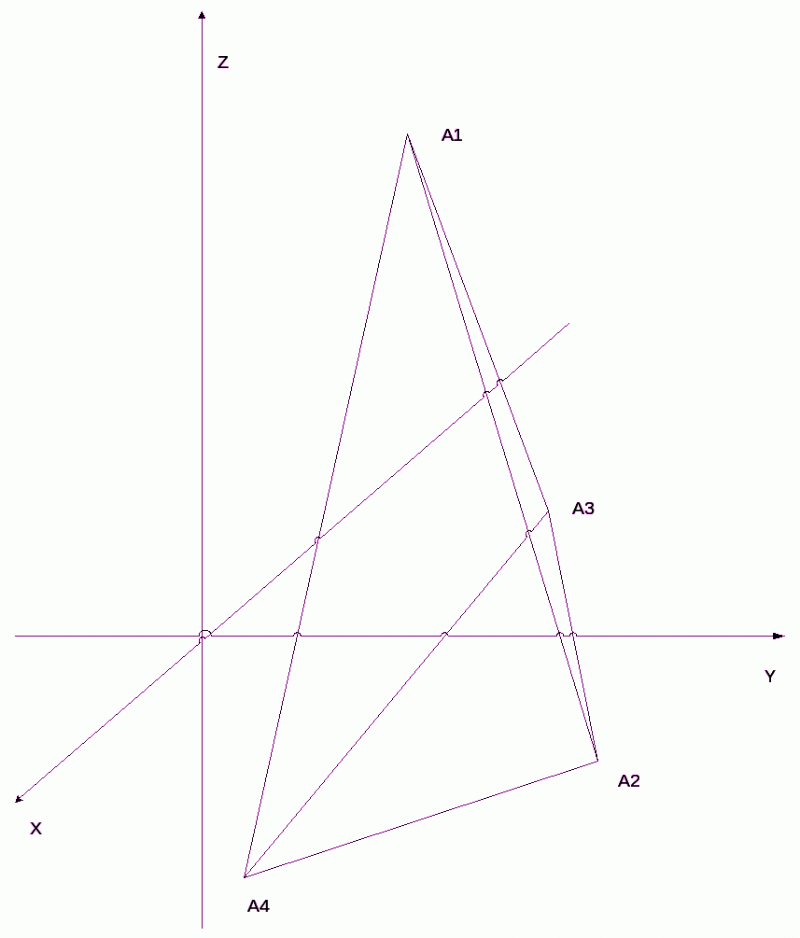
Длина ребра равна расстоянию между точками  и
и  или модулю вектора
или модулю вектора 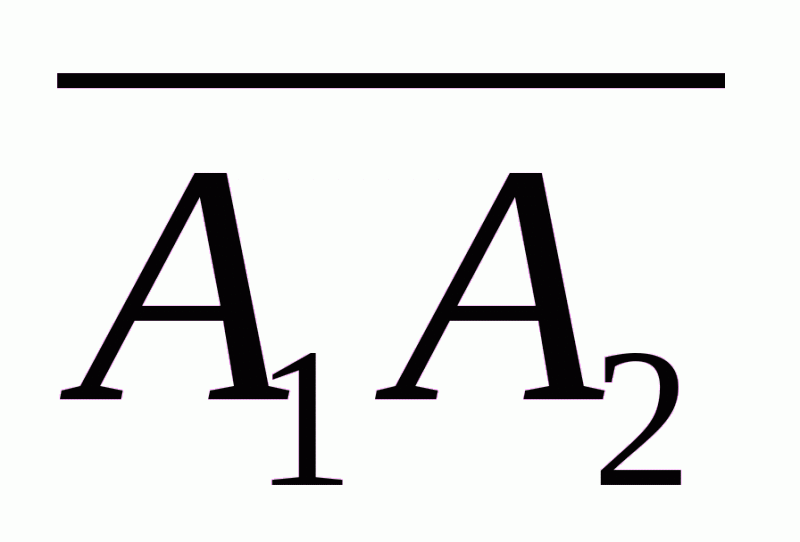 . Расстояние между точками
. Расстояние между точками 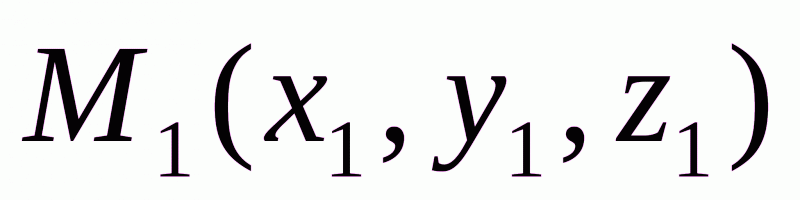 и
и 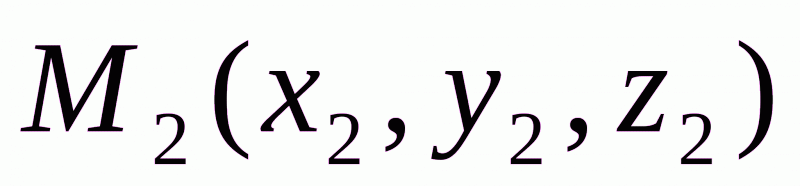 вычисляется по формуле
вычисляется по формуле 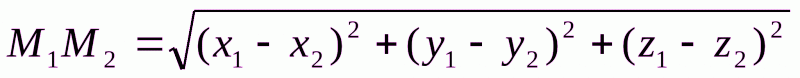 . Подставляя в эту формулу исходные данные, получим
. Подставляя в эту формулу исходные данные, получим 
Угол между ребрами будем искать, используя формулы векторной алгебры:
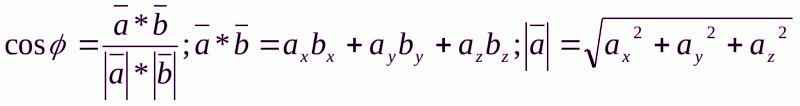
В нашем случае: 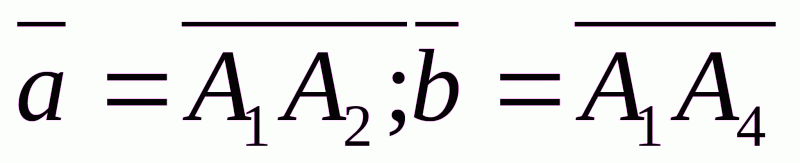
Чтобы найти координаты вектора, из координат конца вектора следует вычесть координаты начала вектора. Таким образом,
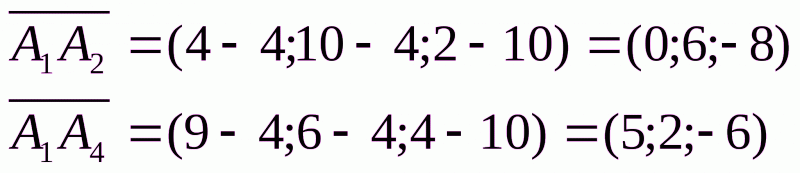
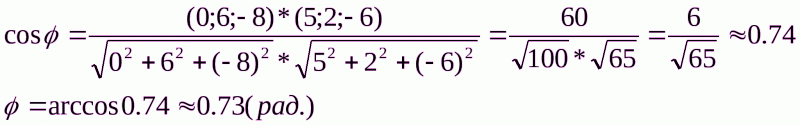
Площадь грани 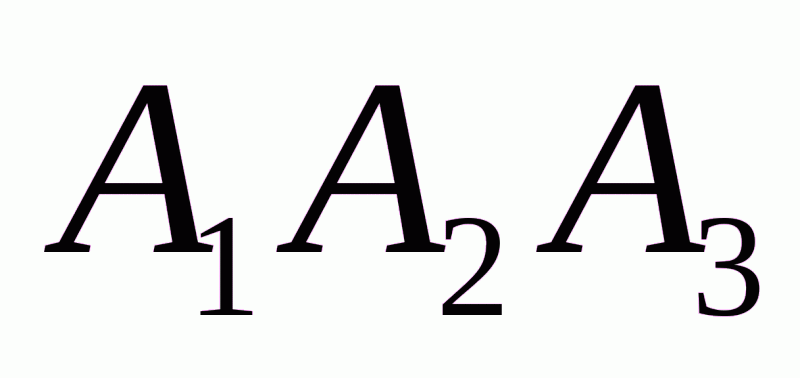 можно найти, используя свойства скалярного произведения: площадь параллелограмма, построенного на векторах
можно найти, используя свойства скалярного произведения: площадь параллелограмма, построенного на векторах  и
и 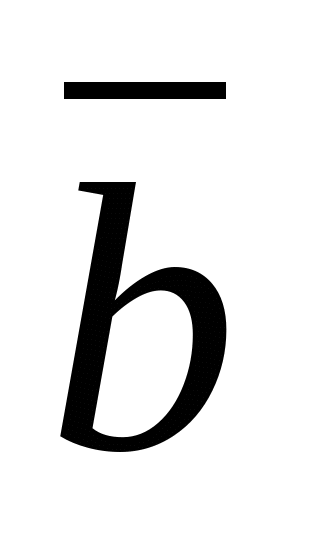 численно равна модулю их векторного произведения. В нашем случае
численно равна модулю их векторного произведения. В нашем случае
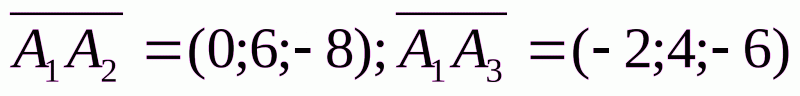
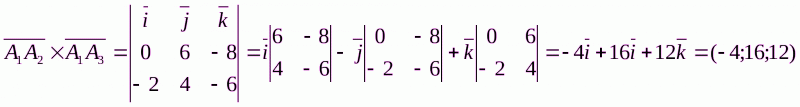
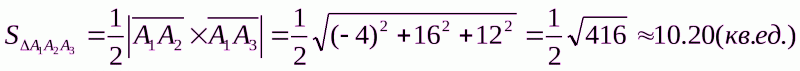
Уравнение плоскости 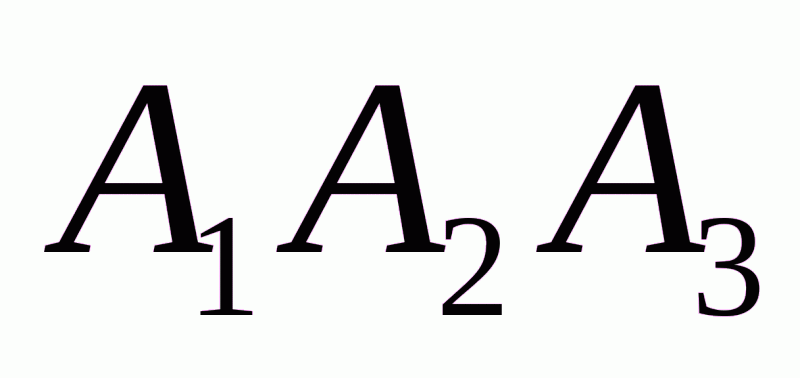 будем искать как уравнение плоскости, проходящей через три данные точки
будем искать как уравнение плоскости, проходящей через три данные точки 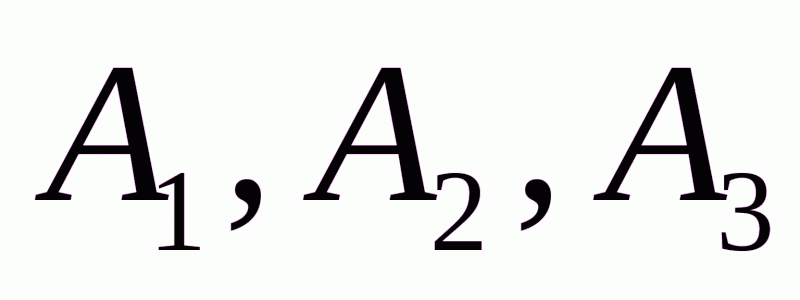 :
:
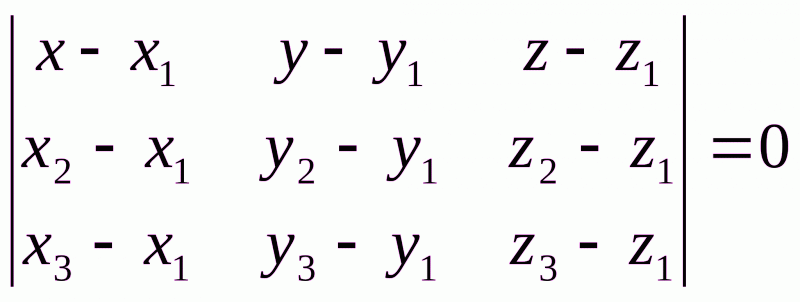 ;
;
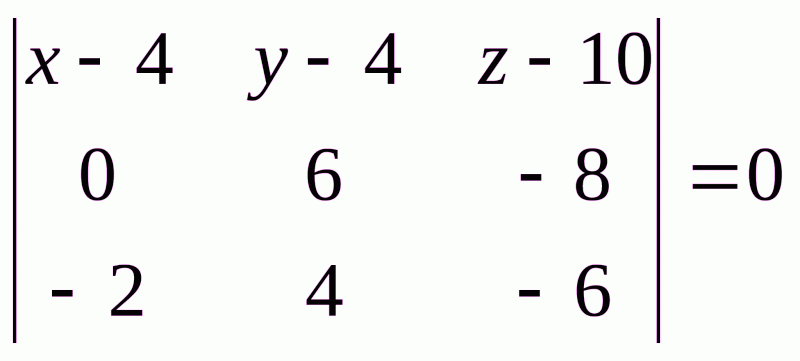 ;
;

Полученное уравнение является уравнением плоскости 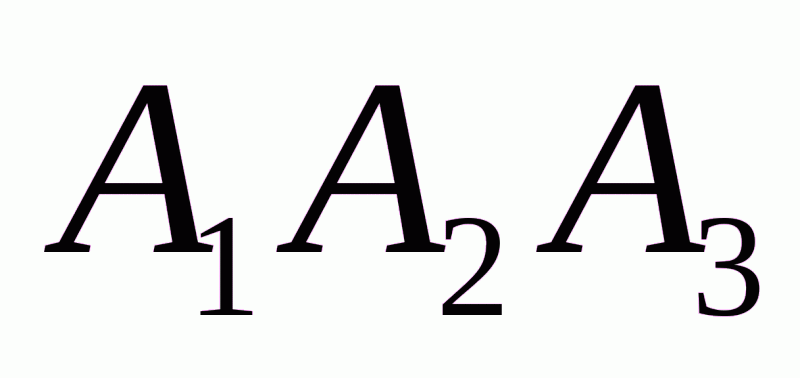 .
.
Объем пирамиды 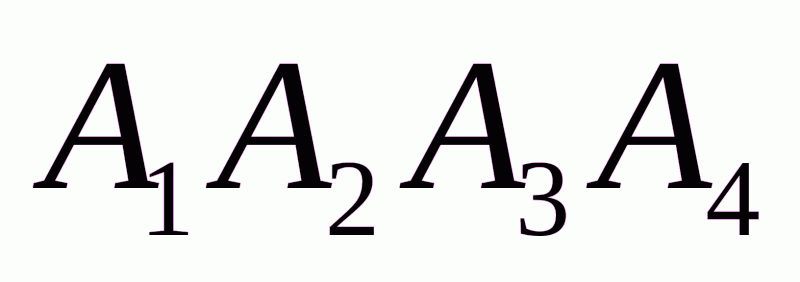 найдем, используя свойство смешанного произведения трех векторов – модуль смешанного произведения численно равен объему параллелепипеда, построенного на этих векторах. Соответственно
найдем, используя свойство смешанного произведения трех векторов – модуль смешанного произведения численно равен объему параллелепипеда, построенного на этих векторах. Соответственно 
Найдем смешанное произведение векторов 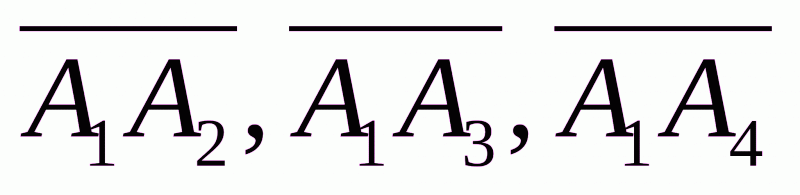 :
:

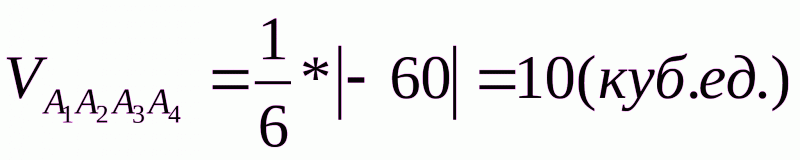
Другие работы по теме:
Жан Батист Жозеф Фурье
Жан Батист Жозеф Фурье. (21.3.1768-16.5.1830) Французский математик,член Парижской АН (1817). Окончив военную школу в Осере, где родился, работал там же преподавателем. В 1796-98 преподавал в Политехнической школе.
работа по праву
Так же на сайте Напишем ру можно заказать курсовые на иностранных языках – английском, французском, немецком, итальянском и других. Регистрация на сайте Напишем ру очень простая и быстрая, оплата производиться любым удобным вам способом – наличными или по электронным платежным системам
Методические рекомендации по подготовке к олимпиадам по математике учащихся 9 классов
Скудина Наталья Федоровна cherlakmg@mail Учитель математики МОУ «Черлакская муниципальная гимназия» Черлакского муниципального района Данные методические рекомендации адресованы учителям математики для подготовки учащихся 9 классов к олимпиаде. Представленный материал включает перечень основных математических понятий, знание которых необходимо участникам олимпиады, а также основные умения и навыки, которые должны быть сформированы у учащихся.
Буль Boole Джордж
Буль (Boole) Джордж (2 ноября 1815, Линкольн, Великобритания - 8 декабря 1864, Баллинтемпль, Ирландия), английский математик и логик, один из основоположников математической логики. Разработал алгебру логики (булеву алгебру) ("Исследование законов мышления", 1854), основу функционирования цифровых компьютеров.
Алгебра и алгебраические системы
Рассматриваются бинарные и n-местные операции, виды бинарных операций, вводятся понятия алгебры, подалгебры, алгебраической системы, приводятся примеры.
Непрерывная, но не дифференцируемая функции
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСУДАРСТВЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «УССУРИЙСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ»
Булевы Функции Функциональная полнота
В алгебре булевых функций P2=<P2;S> S – Операцией является подстановка функции в функцию, суперпозиция. Порождающее множество алгебры P2, принято называть полной системой булевых функций.
Контрольные билеты по алгебре
Алгебра и начала анализа. 11 класс. Билет №1. Функция y = sin x, ее свойства и график. Показательная функция, ее свойства для случая, когда основание больше единицы (доказательство одного из свойств по желанию ученика).
Формулы по алгебре
Основные тригонометрические тождества Формулы суммы и разности Формулы двойного аргумента Формулы произведений Формулы сложения Формулы половинного аргумента
График
Связи между алгеброй и геометрией были известны еще древним математикам. Например, длина отрезка выражается числом, а ведь отрезок — геометрическая фигура, тогда как числа изучаются в алгебре.
Жозеф Луи Лагранж
Лагранж, Жозеф Луи (Lagrange, Joseph Louis) (1736–1813), французский математик и механик.
Логарифмические уравнения
Данная система упражнений может быть использована в качестве дополнения при изучении темы «Логарифмические уравнения» к любому учебнику по алгебре для 10-го класса.
Логические формулы и операции Виды и правила вопросов
Логические операции Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение. Выделяют следующие логические операции: инверсия; конъюнкция; дизъюнкция; импликация; эквиваленция.
Мой любимый предмет - математика сочинение-рассуждение
Автор: Сочинения на свободную тему Я часто думаю, что было бы, если бы мы до сих пор не умели писать и считать. Наверное, жизнь была бы очень скучной и однообразной. Например, я очень люблю головоломки, разные математические задачи. Они помогают мне развиваться, и я всегда радуюсь, когда нахожу правильное решение.
Крамп, Кристиан
Кристиа́н (Кретье́н) Крамп (фр. Christian Kramp, 8 июля 1760, Страсбург — 13 мая 1826, там же) — французский математик (эльзасец). Известен работами по теории чисел, геометрии, математической кристаллографии, алгебре и механике. Предложил общепринятое обозначение n! для факториала.
Шуберт, Фёдор Иванович
Фёдор Иванович (Фридрих Теодор) Шуберт (нем. Friedrich Theodor von Schubert; 1758—1825) — русский математик, астроном, геодезист и популяризатор науки немецкого происхождения.
ГИА алгебра 2009 кодификатор
Государственная (итоговая) аттестация выпускников IX классов общеобразовательных учреждений 2009 г. (в новой форме) по АЛГЕБРЕ Кодификатор элементов содержания по алгебре
Паскаль (Pascal) Блез
Паскаль (Pascal) Блез (19.VI.1623 - 19.VII.1662) - французский математик, физик и философ.
Буль (Boole), Джордж
Его работы «Трактат о дифференциальных уравнениях» (1859г.) и «Трактат о вычислении предельных разностей» (1860г.) оказали колоссальное влияние на развитие математики. В них нашли свое отражение наиболее важные открытия Буля.
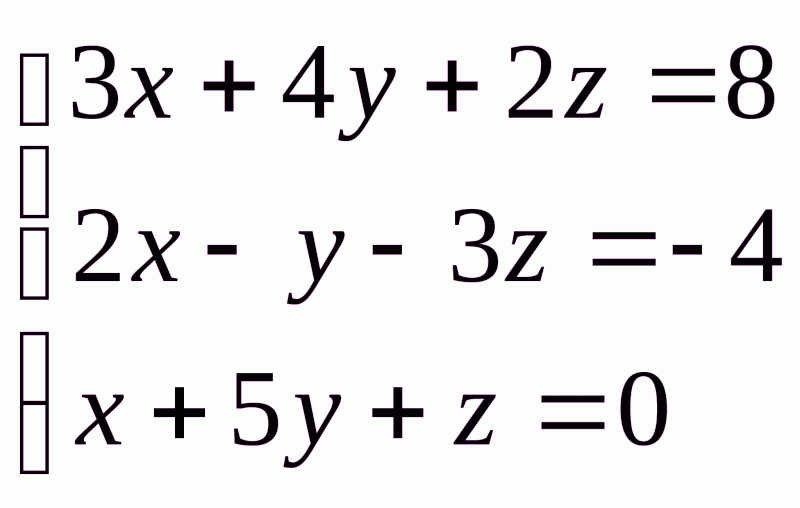
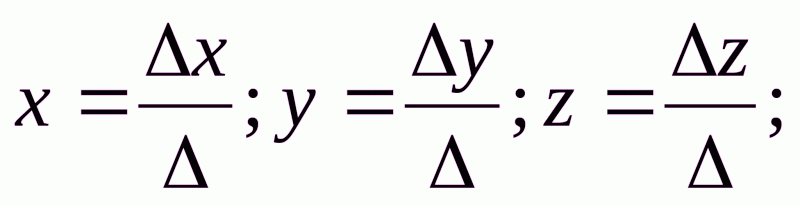
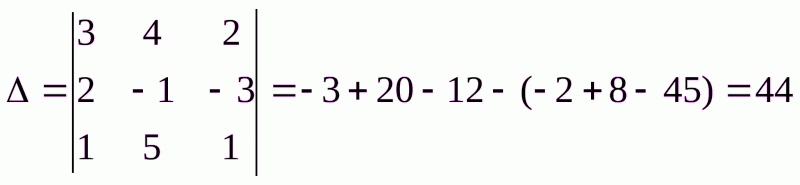
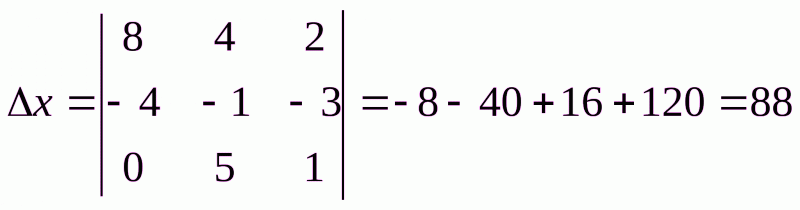
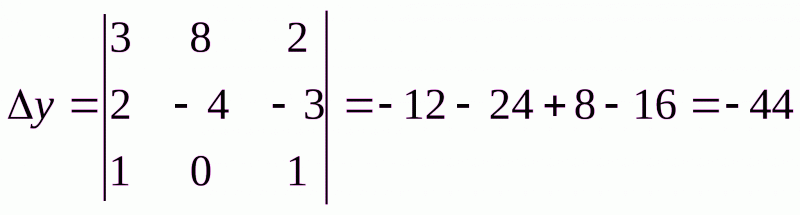
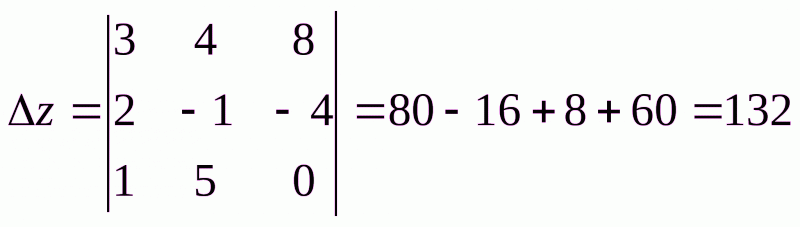
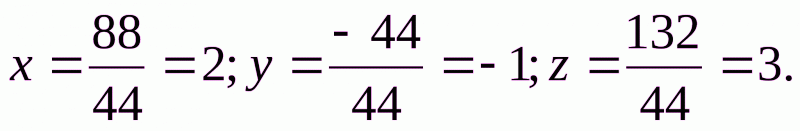
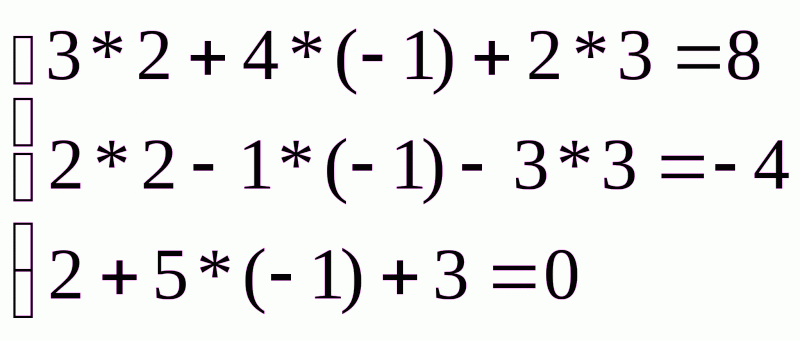

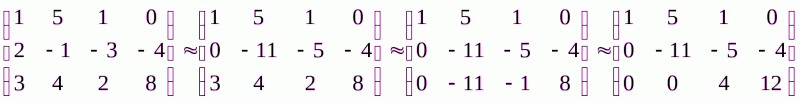
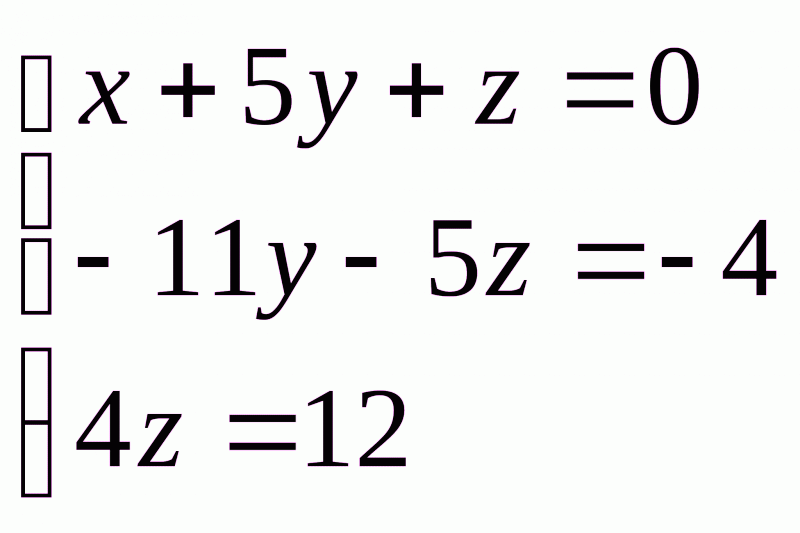
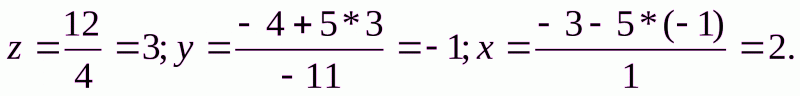
 . Найти:
. Найти: ;
; и
и 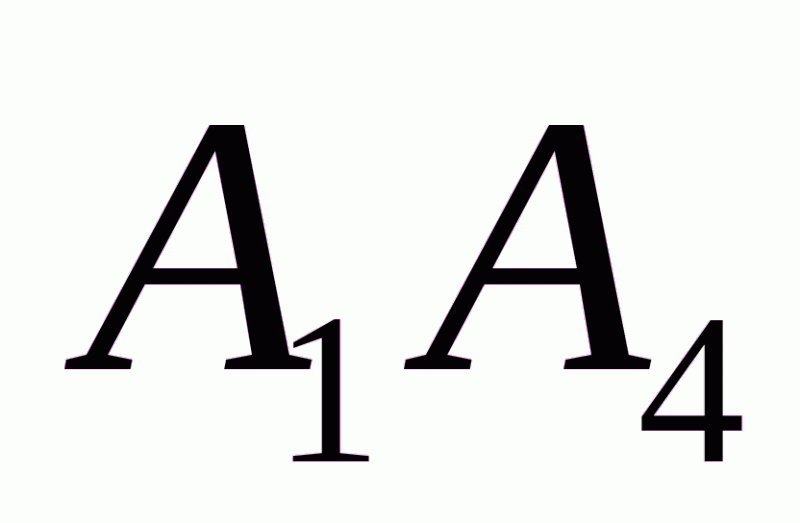 ;
;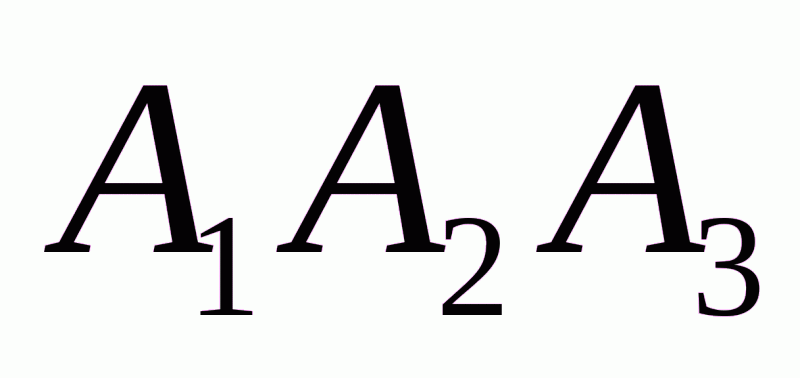 ;
;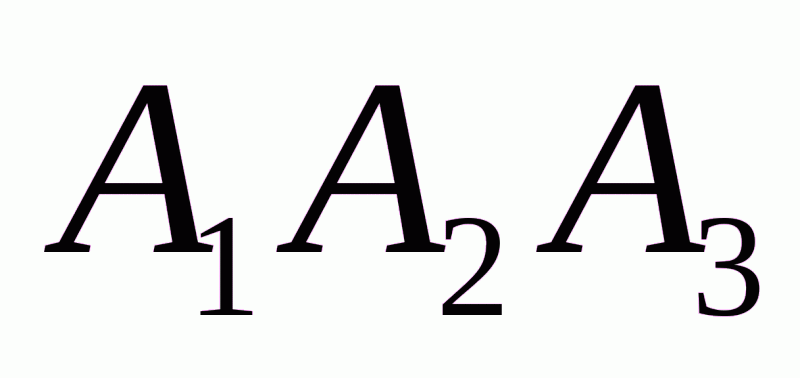 .
. .
.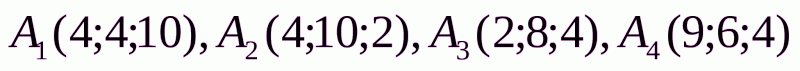

 и
и  или модулю вектора
или модулю вектора 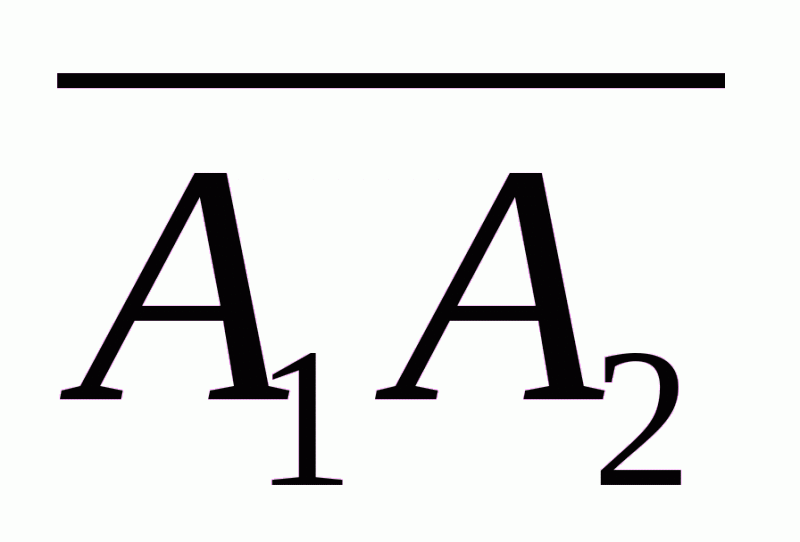 . Расстояние между точками
. Расстояние между точками 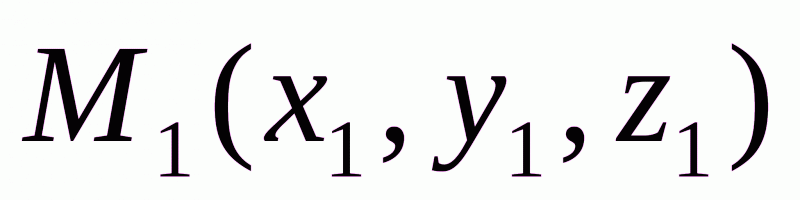 и
и 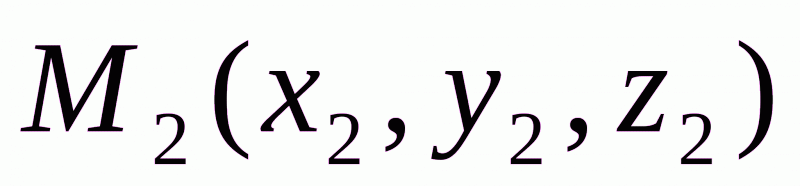 вычисляется по формуле
вычисляется по формуле 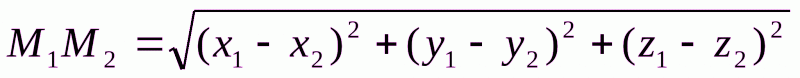 . Подставляя в эту формулу исходные данные, получим
. Подставляя в эту формулу исходные данные, получим 
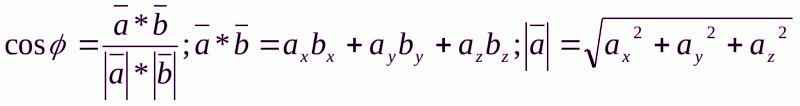
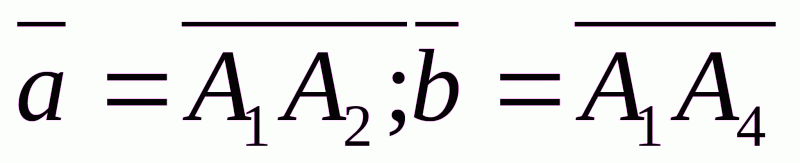
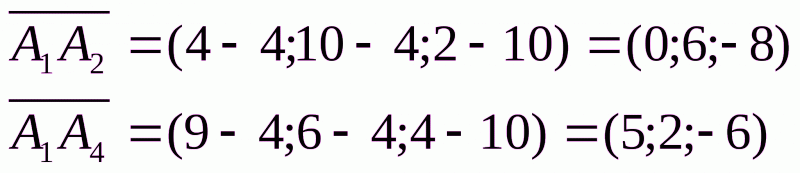
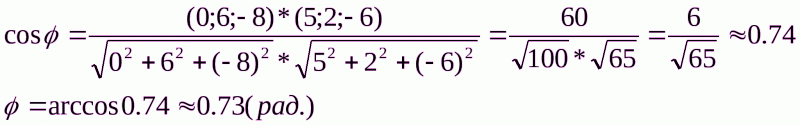
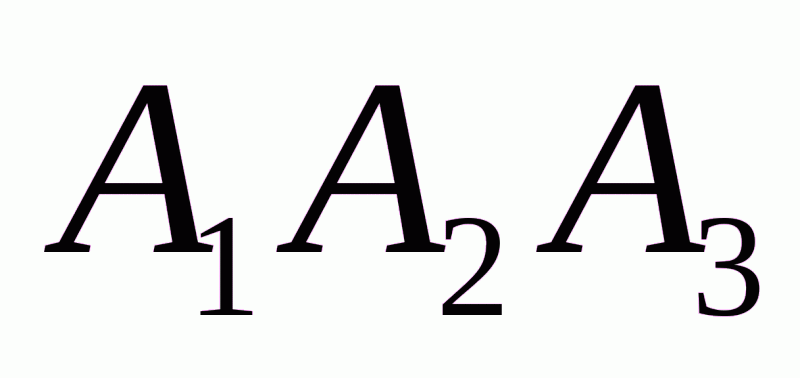 можно найти, используя свойства скалярного произведения: площадь параллелограмма, построенного на векторах
можно найти, используя свойства скалярного произведения: площадь параллелограмма, построенного на векторах  и
и 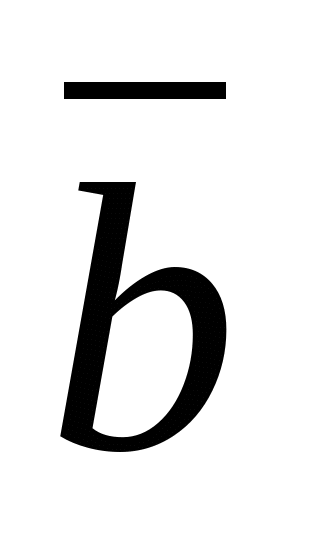 численно равна модулю их векторного произведения. В нашем случае
численно равна модулю их векторного произведения. В нашем случае 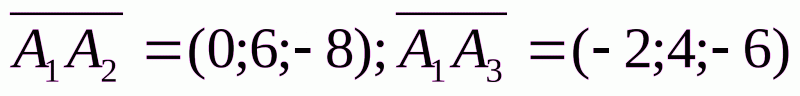
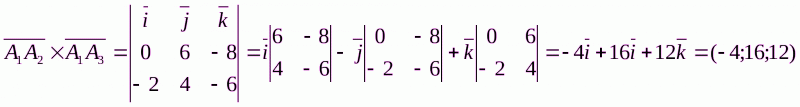
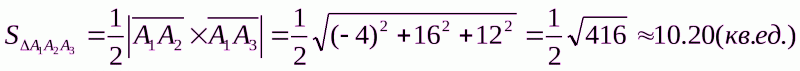
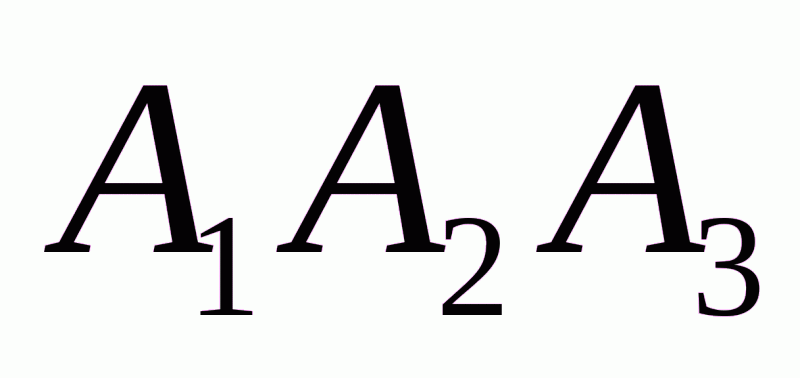 будем искать как уравнение плоскости, проходящей через три данные точки
будем искать как уравнение плоскости, проходящей через три данные точки 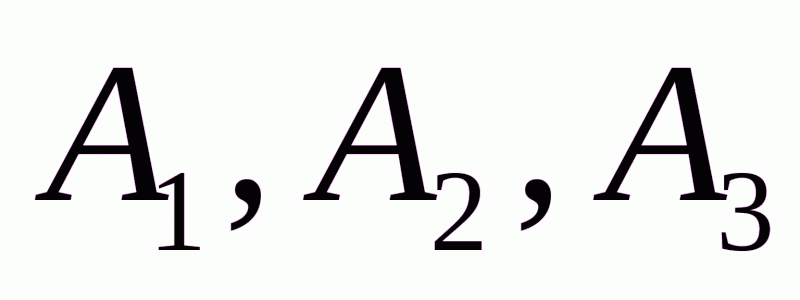 :
: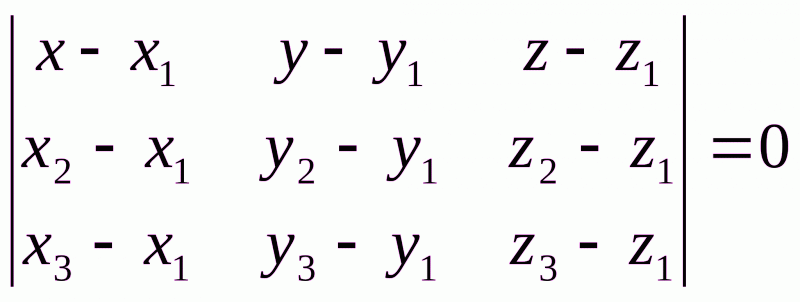 ;
;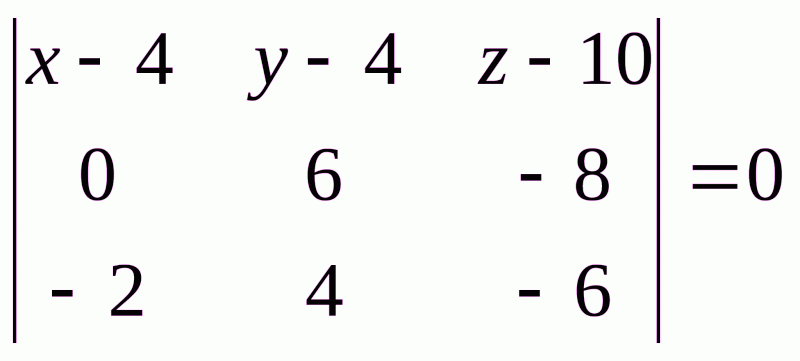 ;
;
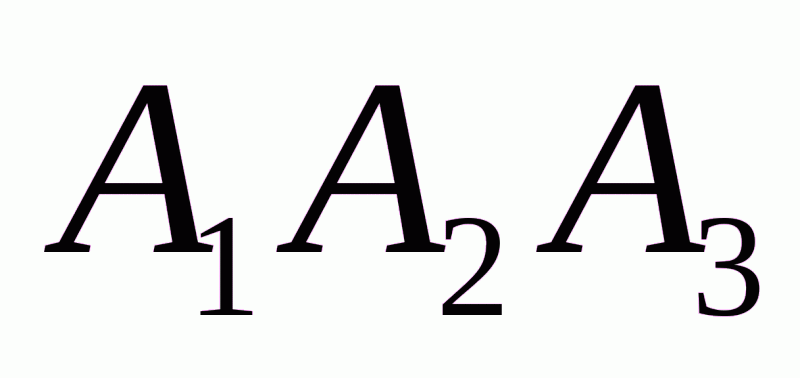 .
.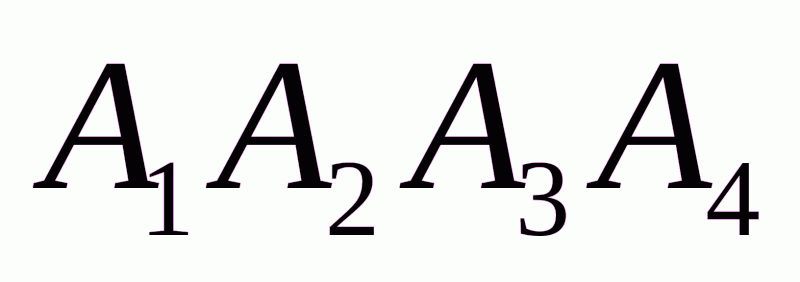 найдем, используя свойство смешанного произведения трех векторов – модуль смешанного произведения численно равен объему параллелепипеда, построенного на этих векторах. Соответственно
найдем, используя свойство смешанного произведения трех векторов – модуль смешанного произведения численно равен объему параллелепипеда, построенного на этих векторах. Соответственно 
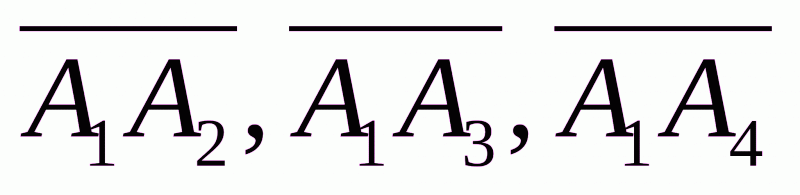 :
: