МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИИ
БИРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ
ФИЗИКО – МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедра МПФ и ТСО
ДИПЛОМНАЯ РАБОТА
Уникальный астрономический объект
SS 433
студентки V курса физико-математического факультета
Рахматуллина Динара Раушановича
Научный руководитель:
Кандидат физико-математических наук доцент Салавенюк Г.М.
Бирск 2004 г.
ОГЛАВЛЕНИЕ
Введение.. 3
Глава 1. Двойные звезды... 5
1.1. Методы изучения физических и оптических визуально-двойных звезд 7
1.2. Спектрально – двойные звезды.. 11
1.3. Затменно–двойные звезды.. 14
1.4. Черные дыры.. 18
Глава 2. Физические процессы в тесных звездных системах 21
2.1. Модели течения вещества в двойных звездах. 23
2.2. Обмен веществом в полуразделенных системах. 25
2.3. Массообмен посредством звездного ветра. 28
2.4. Эволюция одиночной звезды.. 31
2.5. Особенности эволюции звезд в паре. 32
Глава 3. Уникальный объект SS 433. 34
3.1. Загадка SS 433. 34
3.2. Джеты.. 54
3.4. Черная дыра или нейтронная звезда?. 60
3.5. Прецессия джетов. 62
Глава 4. Оценка амплитуды эффекта отражения для рентгеновской звезды звездной системы Her X-1. 64
Заключение.. 68
Литература.. 69
Введение
Двойные звезды весьма часто встречаются в природе, поэтому их изучение существенно не только для выяснения природы самих звезд, но и для космогонических проблем происхождения и эволюции звезд. Двойные звезды не являются редкостью; наоборот, одиночные звезды не входящие в состав двойных систем (или кратных) скорее исключение, чем правило.
Движение компонентов двойных звезд происходит в соответствии с законами Кеплера: оба компонента описывают в пространстве подобные (т. е. одинаковым эксцентриситетом) эллиптические орбиты вокруг общего центра масс. Таким же эксцентриситетом обладает орбита звезды-спутника относительно главной звезды, если последнюю считать неподвижной. Большая полуось орбиты относительно движения спутника вокруг главной звезды равна сумме больших полуосей орбит движения обеих звезд относительно центра масс. С другой стороны, величины больших полуосей этих двух эллипсов обратно пропорциональны массам звезд. Таким образом, если из наблюдений известна орбита относительного движения, то можно определить сумму масс компонентов двойной звезды. Если же известны отношения полуосей орбит движения звезд относительно центра масс, то можно найти еще отношение масс и, следовательно, массу каждой звезды в отдельности, в этом заключается огромная роль изучения двойных звезд в астрономии: оно позволяет определить важную характеристику звезды – массу, знание которой необходимо для исследования внутреннего строения звезды и ее атмосферы.
В двойных и кратных звездных системах вследствие происходящих в них физических процессов (переток вещества с одной компоненты на другую, формирование «шлейфов», общих оболочек, потоков, аккреционных дисков) значительно ускоряется эволюция компонентов (ТДС). Это позволяет глубоко понять физические процессы и эволюцию обычных звезд.
Двойные звезды – единственный способ зарегистрировать черную дыру, если она является одной из компонентов тесной двойной системы.
Цель: рассмотрение физических процессов в тесных двойных системах с релятивистским объектом.
Дипломная работа состоит из введения, четырех глав, заключения и списка литературы, содержащего 24 наименования.
В первой главе говорится о двойных звездах, их классификации (физические и оптические визуально-двойные звезды, спектрально-двойные и затменно-двойные звезды) и черных дырах.
Во второй главе рассматриваются: физические процессы в тесных двойных системах, модели вещества в двойных звездах, обмен веществом в полуразделенных системах, массообмен посредством звездного ветра, особенности эволюции звезд в паре.
Третья глава посвящена уникальному объекту SS 433. Раскрывается в чем же загадка этого объекта, как проявляют себя джеты в диапазонах электромагнитного спектра, модель SS 433, нерешенный вопрос о природе компактного объекта в SS 433 и причина 164-дневной прецессии джетов.
В четвертой главе оценивается амплитуда эффекта отражения для рентгеновской звезды звездной системы Her X-1.
Глава 1. Двойные звезды
Вопрос о спутниках звёзд останется нерешённым до тех пор, пока кто-нибудь, владеющий искусством производить необычайно точные наблюдения, не откроет их.
И.Кеплер. 1610 г.
В середине XVII в. были обнаружены звезды, которые, ничем не отличаясь от других звезд при наблюдениях невооруженным глазом, в телескоп представляются в виде двойных или даже кратных (т. е. тройных или четверных) звезд. Однако впервые серьезное внимание на такие звезды обратил лишь Вильям Гершель, который в 1784 г. составил каталог, содержащий данные наблюдений около 700 двойных и кратных звезд. В. Гершель, основываясь на ряде своих наблюдений одних и тех же двойных звезд, а также на более старых наблюдениях, установил со всей очевидностью наличие орбитальных движений (т. е. движений по орбитам вокруг общего центра масс) у нескольких двойных звезд. Это открытие Гершеля было первым в истории астрономии фактом, показавшим распространение закона всемирного тяготения за пределы солнечной системы (1803 г.).
В. Я. Струве впервые произвел точные измерения расстояний между компонентами двойных звезд и направлений линий, соединяющих компоненты. Он наблюдал свыше 2600 двойных звезд и почти в 100 случаях обнаружил у них орбитальные движения. Каталоги и многочисленные наблюдения двойных звезд В. Я. Струве и его сына О. В. Струве до сих пор имеют огромную ценность.
Двойные звезды носят название визуально-двойных, если их двойственность может быть замечена при непосредственных наблюдениях в телескоп (а в редких случаях и невооруженным глазом, например: x и g Большой Медведицы, находящиеся друг от друга на расстоянии около 12'). В результате работ ряда наблюдателей (среди которых видную роль сыграли работы астрономов Пулковской обсерватории) в каталоги к настоящему времени занесено около 40 000 визуально-двойных звезд.
Применение спектрального анализа привело к открытию в 1889 г. звезд с переменными лучевыми скоростями (линии в спектрах этих звезд периодически смещаются по принципу Доплера – Физо). Изучение этого явления показало, что каждая из таких звезд представляет собой двойную систему, компоненты которой настолько близки друг к другу, что их не удается рассмотреть в отдельности даже при помощи наиболее мощных телескопов. Такие звезды получили название спектрально-двойных.
Еще задолго до открытия спектрально-двойных звезд внимание астрономов привлекла звезда Алголь (b Персея), замечательная правильным наступлением периодов, в течение которых ее блеск уменьшается более чем втрое, а затем снова увеличивается до прежней величины. Изменение блеска Алголя было замечено в 1669 г., а в 1782 г., т. е. более чем 100 лет спустя, глухонемой юноша – любитель астрономии Джон Гудрайк – высказал остроумную догадку, что блеск Алголя изменяется вследствие затмения его темным спутником. Предположение это в дальнейшем получило полное подтверждение. В настоящее время известно почти 2,5 тыс. звезд, блеск которых периодически изменяется по тем же причинам, что и у Алголя. Эти звезды были названы звездами типа Алголя. Они составляют большую часть так называемых затменно-двойных звезд.
Таким образом, известно три типа двойных звезд: визуально-двойные, спектрально-двойные и затменно-двойные. Изучение звезд, входящих в каждый из этих типов, имеет очень важное значение уже потому, что до сих пор только двойные звезды (и, конечно, Солнце) служат источником наших знаний о звездных массах. [5, 24]
1.1. Методы изучения физических и оптических визуально-двойных звезд
Двойные звезды, у которых обнаружено орбитальное движение обоих компонентов вокруг общего центра масс, называются физическими двойными; звезды, у которых наблюдаемая близость компонентов происходит оттого, что эти компоненты, находясь на совершенно различных от нас расстояниях, расположены почти в точности по одному лучу зрения, называются оптическими двойными. В некоторых случаях взаимное линейное расстояние между компонентами физической двойной звезды настолько велико (например, третий компонент звезды Капелла из созвездия Возничего, находящийся на расстоянии 12' от двух ярких компонентов), что их орбитальные движения происходят чрезвычайно медленно. В таком случае судить о том, представляет ли данная двойная звезда физическую или оптическую двойную, можно на основе сравнения собственных движений ее компонентов. Если эти собственные движения близки друг к другу и по величине, и по направлению, значит, двойная звезда физическая, в противном случае–оптическая.
Орбитальное движение физических двойных звезд можно изучать, определяя изменение экваториальных координат обоих компонентов, происходящее с течением времени. Для этой цели можно пользоваться так называемыми абсолютными методами (наблюдение в меридиане), так и дифференциальными методами (например, определяя положение каждого из компонентов относительно фона слабых звезд). Однако проще и точнее можно изучать относительное движение компонентов. С этой целью один из компонентов (обычно более яркий, называемый главной звездой) принимают за неподвижный и изучают относительное движение другого компонента (менее яркого, называемого спутником). При этом с помощью окулярного микрометра или по фотографическому снимку измеряют две величины: расстояние между компонентами, обозначаемое буквой р и выражаемое в секундах дуги, так называемый позиционный угол Q между направлением от главной звезды к северному полюсу мира и линией, соединяющей главную звезду со спутником. Угол Q отсчитывается от направления к полюсу мира
 |
против хода часовой стрелки от 0 до 360°.
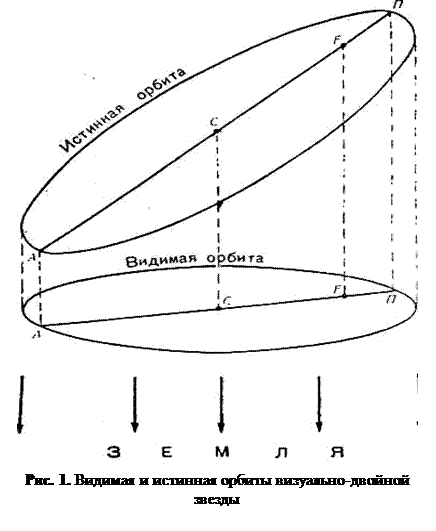
Если повторять такие измерения одной и той же двойной звезды спустя достаточно продолжительные промежутки времени, можно, получив ряд положений спутника относительно главной звезды, определить сначала видимую, а затем и истинную орбиты спутника.
Некоторые из двойных звезд чрезвычайно красивы вследствие резкого различия в окраске компонентов. Так, у двойной звезды g Андромеды главная звезда оранжевая, а спутник голубой. У двойной h Кассиопеи главная звезда желтая, а спутник пурпуровый и т. п. Такая разница в окраске объясняется главным образом причинами физиологического характера (контрастностью) и лишь отчасти зависит от действительного различия цвета компонентов.
Видимые орбиты, спутников визуально-двойных звезд всегда имеют форму эллипса (рис. 1). Однако главная звезда обычно оказывается не в фокусе такого эллипса. Происходит это вследствие того, что истинная орбита спутника рассматривается земным наблюдателем наискось и видимая орбита представляет собой ее проекцию на плоскость, перпендикулярную к лучу зрения. И только в тех редких случаях, когда эта плоскость совпадает с плоскостью истинной орбиты, видимая и истинная орбиты тоже совпадают и главная звезда оказывается в фокусе видимой орбиты спутника.
Построив видимую орбиту, можно определить истинную орбиту. Для этого обычно находят следующие 7 элементов истинной орбиты: T – период обращения, выраженный в годах; t – момент прохождения спутника через периастр (ближайшую к главной звезде точку истинной орбиты); е – эксцентриситет; а – большую полуось орбиты, выраженную в секундах дуги; i–наклонение орбиты, т.е. угол наклона плоскости орбиты к плоскости, перпендикулярной лучу зрения; d – позиционный угол одного из узлов орбиты, т. е. тех двух ее точек, в которых она пересекает плоскость, проходящую через главную звезду и перпендикулярную лучу зрения (обычно берется тот позиционный угол, который меньше 180°); w – угол в плоскости орбиты от узла до периастра, считаемый в направлении движения спутника. [2, 23]
Значительно сложнее обстоит дело с определением орбит кратных звезд в тех случаях, когда три (или более) компонента находятся друг от друга на сравнительно небольших расстояниях и приходится, таким образом, иметь дело с задачей трех тел.
Третий закон Кеплера в форме, полученной Ньютоном для случая движения спутника относительно центрального тела, дает следующее выражение для суммы масс центрального тела и спутника:
![]() , (1.1)
, (1.1)
где k2 – гравитационная постоянная, a – большая полуось орбиты спутника, а T – период его обращения.
Применим выражение для определения суммы масс компонентов визуально-двойной
звезды и напишем подобное выражение для суммы масс Солнца ![]() и Земли
и Земли ![]() :
:
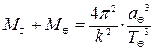 , (1.2)
, (1.2)
где ![]() – астрономическая
единица, а
– астрономическая
единица, а ![]() – период обращения Земли
вокруг Солнца, т. е. звездный год.
– период обращения Земли
вокруг Солнца, т. е. звездный год.
Разделим выражение (1.1) на (1.2), пренебрегая массой Земли из-за ее малости, получим:
 . (1.3)
. (1.3)
Зная величину отношений ![]() и
и ![]() , можно по формуле (1.3) вычислить, во
сколько раз сумма масс компонентов двойной звезды больше массы Солнца.
, можно по формуле (1.3) вычислить, во
сколько раз сумма масс компонентов двойной звезды больше массы Солнца.
Если принять за единицу длины астрономическую единицу, за единицу времени – звездный год (время полного оборота Земли вокруг Солнца) и за единицу массы – массу Солнца, выражение принимает очень простой вид:
![]() .
(1.4)
.
(1.4)
Период Т является одним из семи элементов истинной орбиты,
а большая полуось а связана следующим очевидным соотношением с большой полуосью истинной
орбиты ![]() , выраженной в секундах дуги
и с параллаксом p:
, выраженной в секундах дуги
и с параллаксом p:
![]() . (1.5)
. (1.5)
Если за единицу длины принять астрономическую единицу, то
![]() . (1.6)
. (1.6)
Таким образом, будем ли мы для
вычисления масс пользоваться формулами или более простыми формулами в обоих
случаях, кроме элементов орбиты ![]() и Т,
необходимо знать также и параллакс звезды p.
и Т,
необходимо знать также и параллакс звезды p.
В качестве примера рассмотрим двойную звезду Сириус, для которой отношение
масс компонентов оказалось приблизительно равным 2,5. Элементы Т и ![]() истинной орбиты
спутника относительно главной звезды и параллакс оказались: Т= 50,0 лет,
истинной орбиты
спутника относительно главной звезды и параллакс оказались: Т= 50,0 лет,
![]() = 7",57 и p = 0",375.
= 7",57 и p = 0",375.
Подставляя эти величины в формулы, находим: ![]() = 20,1 и
= 20,1 и ![]() 3,2, а так как
3,2, а так как ![]() :
: ![]() = 2,5, то
= 2,5, то ![]() = 2,3 и
= 2,3 и ![]() = 0,9, т. е. масса спутника
немногим меньше массы Солнца. Известно, что спутник Сириуса является белым карликом.
[16]
= 0,9, т. е. масса спутника
немногим меньше массы Солнца. Известно, что спутник Сириуса является белым карликом.
[16]
1.2. Спектрально – двойные звезды
Звезды, двойственность которых устанавливается лишь на основании спектральных наблюдений, называются спектрально – двойными.
Характер и причина изменения спектров спектрально-двойных звезд объясняются
рис. 2. Если очень близкие компоненты двойной звезды, движущиеся вокруг общего
центра масс, мало отличаются друг от друга по спектру и по бле ску, то в спектре такой звезды должно
наблюдаться периодически повторяющееся раздвоение спектральных линий.
ску, то в спектре такой звезды должно
наблюдаться периодически повторяющееся раздвоение спектральных линий.
Если один компонент занимает положение А1, а другой – положение В1, то оба они будут двигаться под прямым углом к лучу зрения, направленному к наблюдателю, и раздвоения спектральных линии не получится. Но если компоненты занимают положение А2 и В2, то компонент А движется к наблюдателю, а компонент В – от наблюдателя и раздвоение спектральных линий наблюдаться будет, так как у первого компонента спектральные линии сместятся к фиолетовому концу спектра, а у второго – к красному концу. Затем при дальнейшем движении компонентов раздвоение спектральных линий постепенно исчезнет (оба компонента будут опять двигаться под прямым углом к лучу зрения) и снова повторится, когда компонент А будет двигаться от наблюдателя, а компонент В – к наблюдателю. Таким образом, спектральные линии компонентов А и В будут колебаться около некоторых средних своих положений, при которых они будут совпадать и которые соответствуют лучевой скорости центра масс системы.
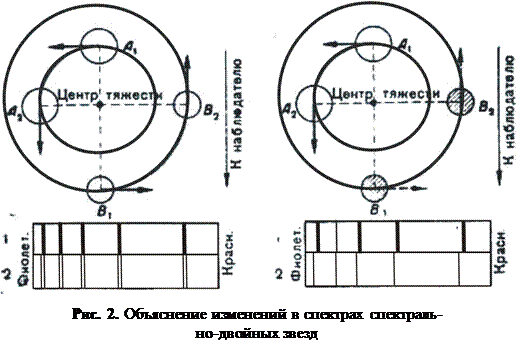 |
В случае же, если один из компонентов значительно уступает по блеску другому (правая часть рис. 2), раздвоение спектральных линий наблюдаться не будет (из-за слабости спектра спутника), но линии спектра главной звезды колебаться будут так же, как и в первом случае.
 |
Периоды изменений, происходящих в спектрах спектрально-двойных звезд, очевидно, являющиеся и периодами их обращения, бывают весьма различны. Наиболее короткий из известных периодов 2,4Ч (g Малой Медведицы), а наиболее длинные – десятки лет.
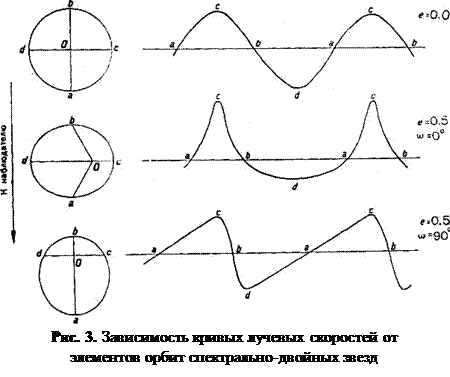
Для определения элементов орбиты какой-либо спектрально-двойной звезды необходимо иметь достаточно большое количество спектрограмм этой звезды, дающих возможность построить так называемую кривую лучевых скоростей. При построении этой кривой по оси абсцисс откладывается время, а по оси ординат – лучевые скорости. Форма кривой лучевых скоростей зависит только от двух элементов – эксцентриситета е и угла w, определяющего положение периастра. Характерные образцы кривых лучевых скоростей для некоторых частных значений е и w изображены на рисунке 3. Положение горизонтальной прямой у всех кривых этого рисунка соответствует лучевой скорости, которую компоненты имеют при своем движении под прямым углом к лучу зрения (т.е., иными словами, лучевой скорости центра масс системы).
Независимо от применяемого
способа из числа элементов орбит спектрально-двойных звезд могут быть определены
только w, ![]() ,
Т и t. Совершенно нельзя определить позиционный
угол и нельзя определить в отдельности наклонение i плоскости орбиты и большую полуось а, так как одни и те же
лучевые скорости могут получиться при движении звезды по орбитам с различными наклонениями
и соответственно различными большими полуосями. [2, 4, 23]
,
Т и t. Совершенно нельзя определить позиционный
угол и нельзя определить в отдельности наклонение i плоскости орбиты и большую полуось а, так как одни и те же
лучевые скорости могут получиться при движении звезды по орбитам с различными наклонениями
и соответственно различными большими полуосями. [2, 4, 23]
1.3. Затменно–двойные звезды
Затменными переменными называются неразрешимые в телескопы тесные пары звезд, видимая звездная величина которых меняется вследствие периодически наступающих для земного наблюдателя затмений одного компонента системы другим. В этом случае звезда с большей светимостью называется главной, а с меньшей – спутником. Типичными примерами звезд этого типа являются звезды Алголь (b Персея) и b Лиры. Вследствие регулярно происходящих затмений главной звезды спутником, а также спутника главной звездой суммарная видимая звездная величина затменных переменных звезд меняется периодически.
Разность звездных величин в минимуме и максимуме называется амплитудой, а промежуток времени между двумя последовательными максимумами или минимумами – периодом переменности. У Алголя, например, период переменности равен 2d20h49m, а у b Лиры– 12d21h48m.
По характеру кривой блеска затменной переменной звезды можно найти элементы орбиты одной звезды относительно другой, относительные размеры компонентов, а в некоторых случаях даже получить представление об их форме. На рис. 4 показаны кривые блеска некоторых затменных переменных звезд вместе с полученными на их основании схемами движения компонентов. На всех кривых заметны два минимума: глубокий (главный, соответствующий затмению главной звезды спутником), и слабый (вторичный), возникающий, когда главная звезда затмевает спутник.
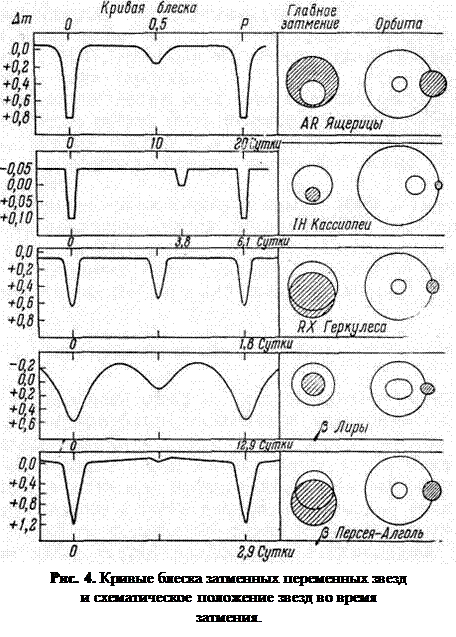 |
На основании детального изучения кривых блеска можно получить следующие данные о компонентах затменных переменных звезд:
1. Характер затмений (частное, полное или центральное) определяется наклонением i и размерами звезд. Когда i = 90°, затмение центральное, как у b Лиры (рис. 5). В тех случаях, когда диск одной звезды полностью перекрывается диском другой, соответствующие области кривой блеска имеют характерные плоские участки (как у IH Кассиопеи), что говорит о постоянстве общего потока излучения системы в течение некоторого времени, пока меньшая звезда проходит перед или за диском большей. В случае только частных затмений минимумы острые (как у RX
 |
Геркулеса или b Персея).
2. На основании продолжительности минимумов находят радиусы компонентов R1 и R2, выраженные в долях большой полуоси орбиты, так как продолжительность затмения пропорциональна диаметрам звезд.
3. Если затмение полное, то по отношению глубин минимумов можно найти отношение светимостей, а при известных радиусах,– также и отношение эффективных температур компонентов.
4. Отношение промежутков времени от середины главного минимума до
середины вторичного минимума и от вторичного минимума до следующего главного
минимума зависит от эксцентриситета орбиты е и долготы периастра w. Точнее, фаза наступления вторичного минимума зависит от произведения ![]() . Если вторичный минимум лежит посередине между
двумя главными минимумами (как у RX
Геркулеса), то орбита симметрична относительно луча зрения и, в частности,
может быть круговой. Асимметрия положения вторичного минимума позволяет найти
произведение
. Если вторичный минимум лежит посередине между
двумя главными минимумами (как у RX
Геркулеса), то орбита симметрична относительно луча зрения и, в частности,
может быть круговой. Асимметрия положения вторичного минимума позволяет найти
произведение ![]() .
.
5. Наклон кривой блеска, иногда наблюдаемый между минимумами, позволяет количественно оценить эффект отражения одной звездой излучения другой, как, например, у b Персея.
6. Плавное изменение кривой блеска, как, например, у b Лиры, говорит об эллипсоидальности звезд, вызванной приливным воздействием очень близких компонентов двойных звезд. К таким системам относятся звезды типа b Лиры и W Большой Медведицы (см. рис. 5). В этом случае по форме кривой блеска можно установить форму звезд.
7. Детальный ход кривой блеска в минимумах иногда позволяет судить о законе потемнения диска звезды к краю. Выявить этот эффект, как правило, очень трудно. Однако это единственный имеющийся в настоящее время метод изучения распределения яркости по дискам звезд.
В итоге на основании вида кривой блеска затменной переменной
звезды в принципе можно определить следующие элементы и характеристики системы:
i – наклонение орбиты; Т – период; ![]() – эпоху главного минимума; е
– эксцентриситет орбиты; w –
долготу периастра; R1 и R2 – радиусы компонентов, выраженные в долях
большой полуоси; для звезд типа b Лиры – эксцентриситеты эллипсоидов, представляющих форму звезд; L1/L2 – отношение светимостей компонентов или их температур
– эпоху главного минимума; е
– эксцентриситет орбиты; w –
долготу периастра; R1 и R2 – радиусы компонентов, выраженные в долях
большой полуоси; для звезд типа b Лиры – эксцентриситеты эллипсоидов, представляющих форму звезд; L1/L2 – отношение светимостей компонентов или их температур ![]() .
.
В настоящее время известно свыше 4000 затменных переменных звезд различных типов. Минимальный известный период – около часа, наибольший – 57 лет. Информация о затменных звездах становится более полной и надежной при дополнении фотометрических наблюдений спектральными. [4,6].
1.4. Черные дыры
Считается, что, если масса звезды больше 2,5 ![]() , то в конце своей эволюции
эта звезда превратится в черную дыру.
, то в конце своей эволюции
эта звезда превратится в черную дыру.
Черной дырой называется релятивистский объект, в котором гравитационное поле настолько сильно, что даже свет не может покинуть эту область. Это происходит, если размеры тела меньше его гравитационного радиуса
![]() , (1.7)
, (1.7)
 |
где G – постоянная тяготения Ньютона, с – скорость света, М – масса тела. Гравитационный радиус Солнца – 3 км, Земли – около 9 мм. [18]
Как возникают черные дыры?
Известно, что если масса ядра звезды,
претерпевшего изменение химического состава из-за термоядерных реакций и
состоящего в основном из элементов группы железа, превышает 1,4 ![]() , но не превосходит 3
, но не превосходит 3![]() ,
то происходит коллапс ядра, в результате которого звезда сбрасывает внешнюю
оболочку. Это приводит к вспышке сверхновой и образованию нейтронной звезды. В
такой звезде силам гравитации противостоит давление вырожденного нейтронного
вещества. Радиопульсары и рентгеновские пульсары как раз и представляют собой
нейтронные звезды. Первые наблюдаются как источники периодических
радиоимпульсов, что связано с переработкой сильным магнитным полем нейтронной
звезды энергии вращения в направленное радиоизлучение.
,
то происходит коллапс ядра, в результате которого звезда сбрасывает внешнюю
оболочку. Это приводит к вспышке сверхновой и образованию нейтронной звезды. В
такой звезде силам гравитации противостоит давление вырожденного нейтронного
вещества. Радиопульсары и рентгеновские пульсары как раз и представляют собой
нейтронные звезды. Первые наблюдаются как источники периодических
радиоимпульсов, что связано с переработкой сильным магнитным полем нейтронной
звезды энергии вращения в направленное радиоизлучение.
Рентгеновские пульсары светят за счет аккреции вещества в тесных двойных системах: магнитное поле нейтронной звезды направляет плазму на полюса, где она сталкивается с поверхностью нейтронной звезды и разогревает ее до температуры в десятки миллионов градусов. Это приводит к излучению рентгеновских квантов. Поскольку горячие рентгеновские пятна на магнитных полюсах вращающейся нейтронной звезды периодически бывают обращены к наблюдателю, он видит строго периодические пульсации интенсивности рентгеновского излучения [19]. Периодические пульсации радио- или рентгеновского излучения говорят о том, что у нейтронной звезды есть твердая поверхность, сильное магнитное поле и быстрое вращение. У черной дыры строго периодических пульсаций излучения ожидать не приходится, поскольку она не имеет ни твердой поверхности, ни магнитного поля.
Звездам, массы железных ядер которых превышают 3![]() , ОТО предсказывает
в конце эволюции неограниченное сжатие с образованием черной дыры. Это
объясняется тем, что силы гравитации, стремящиеся сжать звезду, определяются
плотностью энергии, а при громадных плотностях вещества, достигаемых при сжатии
ядра звезды, главный вклад в плотность энергии вносит уже не энергия покоя
частиц, а энергия их движения и взаимодействия. Получается, что давление
вещества при очень больших плотностях как бы само становится весомым. Чем
больше давление, тем больше плотность энергии и, следовательно, больше силы
гравитации, стремящиеся сжать вещество. Кроме того, при сильных гравитационных
полях, согласно ОТО, становятся принципиально важными эффекты искривления
пространства-времени, что также способствует неограниченному сжатию вещества.
[18, 20]
, ОТО предсказывает
в конце эволюции неограниченное сжатие с образованием черной дыры. Это
объясняется тем, что силы гравитации, стремящиеся сжать звезду, определяются
плотностью энергии, а при громадных плотностях вещества, достигаемых при сжатии
ядра звезды, главный вклад в плотность энергии вносит уже не энергия покоя
частиц, а энергия их движения и взаимодействия. Получается, что давление
вещества при очень больших плотностях как бы само становится весомым. Чем
больше давление, тем больше плотность энергии и, следовательно, больше силы
гравитации, стремящиеся сжать вещество. Кроме того, при сильных гравитационных
полях, согласно ОТО, становятся принципиально важными эффекты искривления
пространства-времени, что также способствует неограниченному сжатию вещества.
[18, 20]
Глава 2. Физические процессы в тесных звездных системах
Если две звезды образуют достаточно тесную систему, такую, что расстояние между звездами сравнимо с их радиусами, взаимодействие звезд-партнеров не ограничивается только тем, что они вращаются вокруг общего центра тяжести. Очень важно, что в этом случае возможно перетекание вещества с одной звезды на другую под действием гравитационного притяжения.
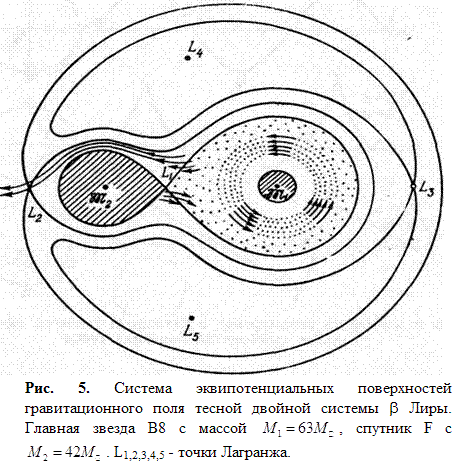
Каждая звезда в тесной паре имеет свою «зону влияния», в пределах которой преобладает ее, а не партнера, собственное тяготение. Эту зону называют полостью Роша (по имени французского астронома XIX века, который изучал взаимное тяготение планет и их спутников, но построил и общую теорию, применимую к двойным звездам).
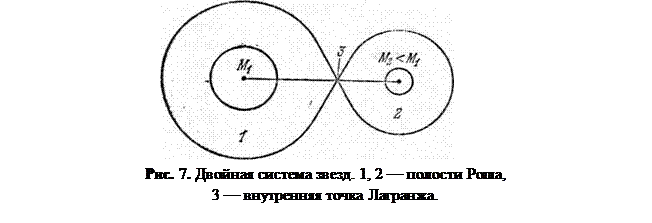
Эти зоны должны, очевидно,
соприкасаться в одной точке на линии, соединяющей центры звезд: в ней сила
тяготения отсутствует, ибо одна звезда создает в ней силу тяготения, точно
такую же по величине, что и другая, по противоположную по направлению (рис.7).
Для этой точки тоже есть специальное название – внутренняя точка Лагранжа (по
имени другого французского ученого, знаменитого математика и механика XVIII – начала XIX вв.). Если массы звезд одинаковы, то точка Лагранжа лежит
посередине между ними; если массы разные, то она, естественно, ближе к менее
массивной звезде, так как полость Роша тем обширнее, чем больше масса звезды.
Обмен веществом между звездами возможен двумя путями: либо «звездный ветер» проникает из полости Роша «своей» звезды в полость Роша звезды-компаньона, либо одна из звезд, так сказать, переполняет свою полость Роша.
Звездный ветер был открыт, прежде всего, у Солнца (солнечный ветер); оказалось, что происходит непрерывное истечение плазмы солнечной короны в межпланетное пространство. У более массивных и горячих, чем Солнце, звезд потоки плазмы интенсивнее; они имеют вполне достаточные скорости и достаточный запас кинетической энергии, чтобы навсегда покинуть звезду, преодолев ее притяжение. В двойной системе какая-то часть частиц, покинувших одну звезду, может быть захвачена полем тяготения другой звезды.
Гораздо большие порции вещества могут перейти от одной звезды к другой на втором пути, когда дело не ограничивается истечением из короны звезды. Значительный переброс вещества от одной звезды к другой способен очень существенно повлиять на характер дальнейшей эволюции обеих звезд в тесной паре.[10]
Многие интересные черты процессов такого рода выяснены в работах А.Г. Масевич, А.В. Тутукова и Л.Р. Юнгельсона. Более массивная из двух звезд пары первой переходит на ту стадию эволюции, на которой происходит сброс оболочки. Значительную долю вещества этой оболочки способна захватить вторая, менее массивная звезда; но, увеличив массу за счет вещества своего партнера, эта звезда станет теперь более массивной, и потому темп ее эволюции возрастет. Вскоре и она начнет расширяться, причем размеры ее оболочки станут столь значительными, что внутри этой оболочки окажется и остаток первой звезды, успевший уже превратиться в нейтронную звезду. Последняя, двигаясь в среде оболочки, тормозится (как спутник в плотных слоях земной атмосферы), приближается из-за этого к ядру второй звезды и в конце концов образует вместе с ним тесное двойное ядро внутри обширной единой оболочки. Такие объекты – две компактные звезды в общей оболочке – обнаружены прямыми астрономическими наблюдениями. [4]
2.1. Модели течения вещества в двойных звездах
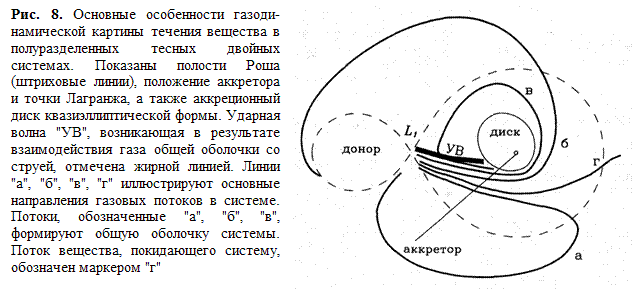 |
Для расчета течения вещества в двойных звездах обычно используют уравнения газодинамики, описывающие поведение инертного газа под действием гравитационных, радиационных и магнитных полей. Численное рассмотрение трехмерных течений было до недавнего времени затруднено отсутствием надлежащей вычислительной техники и даже теперь оно ограничено скудностью ресурсов. Поэтому теоретики вынуждены были ограничиться расчетами для двумерных газодинамических моделей. При этом предполагалось, что решение, полученное для экваториальной плоскости, отражает общие особенности структуры течения. Немногочисленные расчеты конкретных двойных систем, проведенные в последнее время в рамках трехмерных моделей, подтверждают, что характерные особенности течения, обнаруженные в упрощенных двумерных моделях, качественно остаются неизменными. [3]
Двойные системы (без
сильного магнитного поля) можно разделить на три класса в зависимости от
механизма массообмена и его типичных параметров. К первому типу относятся
системы, в которых процесс массопереноса происходит через окрестность внутренней точки Лагранжа ![]() (полуразделенные двойные
системы).
(полуразделенные двойные
системы).
Рассмотрим двойную систему звезд. По какой орбите движется материальная точка, оказавшаяся в окрестностях этой системы? Пока она близка к одному из компонентов, ее движение определяется тяготением этого компонента. Частицы движутся по коническим сечениям (эллипс, парабола, гипербола). По мере удаления от одной звезды и приближения к другой потенциал, создаваемый одной звездой, уменьшается, а другой - растет. И где-то на линии, соединяющей звезды, существует точка, где силы притяжения двух звезд и центробежная сила уравновешены. Частица, попавшая в эту точку, может свободно перейти из поля действия одной звезды в поле действия другой. Это и есть внутренняя точка Лагранжа L1. Участки пространства вокруг каждой звезды, заключенные внутри эквипотенциальной поверхности с потенциалом, равным потенциалу в точке Лагранжа, называются полостью Роша данной звезды. Процесс массообмена может быть весьма интенсивным, если одна звезда (донор) находится в процессе перехода в красный гигант и заполняет свою полость Роша.
Ко второму и третьему типам относятся системы, в которых массообмен определяется звездным ветром. Структура течения в этом случае сильно зависит от отношения W скорости ветра к орбитальной скорости системы, поэтому и пришлось ввести два варианта таких систем: с отношением W»£1 (второй тип), и W>1 (третий тип). [3]
2.2. Обмен веществом в полуразделенных системах
В полуразделенной ТДС одна из звезд заполнила критическую поверхность Роша. Эта звезда - донор; вторая, в конечном счете поглощающая значительную долю вещества, потерянного первой, - аккретор. Обмен веществом происходит через окрестность внутренней точки Лагранжа L1. Газодинамику истечения вещества из окрестностей точки L1 неоднократно исследовали многие авторы. Впервые анализ данной проблемы, полученный в полуаналитическом приближении, представлен в работах Б. Пачинского и Р. Сенкевича, а также С. Любова и Ф. Шу в начале 70-х годов. Детальное исследование процесса обмена веществом в двойных звездах аналитическими методами затруднено, поскольку процесс очень сложный, в частности, необходимо учитывать взаимодействие струи вещества, проходящей в окрестностях точки Лагранжа, с окружающей средой. Нелинейный характер такого взаимодействия приводит к необходимости решения полной системы газодинамических уравнений для описания процессов, происходящих в полуразделенных двойных.
Рассмотрим теперь результаты исследований, выполненных в рамках трехмерной модели. Расчеты были сделаны для типичных представителей маломассивных рентгеновских и катаклизмических двойных. Катаклизмические переменные – системы, состоящие из маломассивной звезды главной последовательности и белого карлика с коротким (несколько часов) периодом орбитального обращения. Помимо изменений блеска, вызванных орбитальным движением, у них наблюдаются различные виды вспышечной активности.
Полученные результаты свидетельствуют о качественно похожем характере течения в исследуемых системах. Выявлены следующие особенности процесса:
1) вещество струи разделяется на три потока: первый формирует квазиэллиптический аккреционный диск вокруг звезды-аккретора; второй огибает аккретор вне диска; третья часть струи удаляется от обеих звезд, однако значительная доля вещества этого потока в дальнейшем меняет направление своего движения под действием силы Кориолиса и остается в системе;
2) взаимодействие струи и диска не является ударным.
Часть вещества струи сразу попадает в диск и в дальнейшем, теряя угловой момент под действием вязкости, участвует в процессе аккреции. Полученные количественные оценки показывают, что в стационарном режиме течения доля аккрецируемого вещества составляет весьма значительную долю (вплоть до 75%) от общего количества газа, вбрасываемого в систему звездой-донором.
Гипотеза "горячего пятна", образуемого, якобы, в месте предполагаемого удара истекающей из донора струи об аккреционный диск, была предложена ранее для объяснения сложной картины переменности катаклизмических звезд. Вокруг звезд системы существует общая оболочка из разреженного газа и, как оказалось, взаимодействие газа со струей, вытекающего из окрестности Ц, отклоняет ее. Это приводит к безударному (касательному) контакту струи с наружным краем аккреционного диска и, как следствие, к отсутствию "горячего пятна". В то же время взаимодействие газа общей оболочки со струей приводит к образованию протяженной ударной волны переменной интенсивности, расположенной вдоль края струи. Область высвечивания горячего газа, нагретого ударной волной, лежит вне аккреционного диска, однако основное энерговыделение, вследствие изменения интенсивности ударной волны вдоль струи, происходит в достаточно ограниченной области (60% выделяется в прилегающей к диску части волны). Этот факт, а также приблизительно равные значения скорости энерговыделения и приводили к тому, что гипотеза "горячего пятна" в общем достаточно хорошо удовлетворяла наблюдениям.
Для проверки истинности представленной модели были рассчитаны кривые блеска для катаклизмической двойной Z Хамелеона (Z Cha) и проведено их сравнение с наблюдениями. При построении теоретических кривых блеска использовалась фотометрическая модель, разработанная членом-корреспондентом РАН A.M. Черепащуком и кандидатом физико-математических наук Т.С. Хрузиной. Сравнение наблюдаемой и рассчитанной кривых блеска показывает хорошее согласие. На теоретической кривой можно увидеть практически все основные детали, характерные для наблюдаемой кривой блеска Z Cha. Подобные кривые блеска построены для различных типов катаклизмических двойных. Они показали, что, оставаясь в рамках рассматриваемой модели течения без "горячего пятна", можно объяснить все многообразие наблюдаемых кривых блеска. Более того, в ряде случаев новая модель способна лучше объяснить наблюдения, чем модель с "горячим пятном".
Качественное подобие полученных решений для различных типов полуразделенных систем позволяет говорить об универсальности рассматриваемой модели. Однако все эти результаты получены для установившегося режима течения. Если сильно влияние внешних факторов, возможно возникновение и других особенностей, в частности, областей ударного взаимодействия диска с потоком газа в системе. Например, если диск сформировался еще до заполнения звездой-донором своей полости Роша, то в начале стадии интенсивного обмена массой возможно возникновение горячего пятна в месте соприкосновения струи вещества с наружным краем диска, которое должно исчезнуть после выхода течения на стационарный режим. Интересно определить длительность жизни этого образования. Естественно принять за него время, требуемое для полной замены вещества диска. В случае типичных полуразделенных систем установлено, что для этого достаточно нескольких десятков орбитальных периодов. Следовательно, большую часть времени существования полуразделенных двойных систем картина течения вещества в них описывается представленной выше моделью.
2.3. Массообмен посредством звездного ветра
Наряду с исследованием перетекания газа через внутреннюю точку Лагранжа, внимание астрофизиков все больше привлекает другой возможный механизм обмена веществом в ТДС - посредством звездного ветра. Важность подобных исследований определяется, в частности, тем, что к системам, где истекающая звезда не заполняет свою полость Роша и обмен веществом идет посредством звездного ветра, относятся очень интересные симбиотические и массивные рентгеновские звезды. Проведенные исследования показали, что общая картина течения вещества в подобных системах определяется, в первую очередь, параметрами звездного ветра. Из наблюдений известно, что различные классы объектов, принадлежащих к ТДС с компонентами, не заполняющими полость Роша, могут иметь значительно различающиеся режимы истечения вещества (так, например, в рентгеновских двойных скорости газа в 10-100 раз больше, чем в так называемых симбиотических звездах).
Основываясь на результатах двумерных газодинамических расчетов, попытаемся выяснить общие тенденции изменения картины течения в зависимости от параметров звездного ветра. Это может иметь и практическое значение для анализа наблюдений. В качестве свободного параметра при расчетах введем отношение W скорости ветра к орбитальной скорости аккретора, что позволит использовать полученные результаты при анализе других двойных систем.
Расчеты проведены при
фиксированных параметрах двойной системы: масса первичного - истекающего -
компонента ![]() и радиус
и радиус ![]() , что соответствует
объемной степени заполнения полости Роша в 29.6%; масса вторичного компонента -
компактного объекта -
, что соответствует
объемной степени заполнения полости Роша в 29.6%; масса вторичного компонента -
компактного объекта - ![]() , а радиус
, а радиус ![]() . Орбитальный период T
= 725 дням, расстояние между центрами компонентов
. Орбитальный период T
= 725 дням, расстояние между центрами компонентов ![]() .
Данные параметры двойной системы являются типичными для симбиотических звезд.
Учитывая, что скорость истекающего газа - определяющий параметр при
формировании структуры течения
.
Данные параметры двойной системы являются типичными для симбиотических звезд.
Учитывая, что скорость истекающего газа - определяющий параметр при
формировании структуры течения
 |
вещества, полученные результаты могут быть с определенными оговорками перенесены и на другие системы.
Анализ полученных
результатов показывает, что при больших скоростях ветра (![]() >
>![]() , т.е. W>1)
в двойных системах наблюдается коническая ударная волна, обусловленная прямым
потоком вещества от звезды-донора. Увеличение скорости ветра приводит к уменьшению
раствора конуса и смещению его оси к линии, соединяющей центры звезд.
, т.е. W>1)
в двойных системах наблюдается коническая ударная волна, обусловленная прямым
потоком вещества от звезды-донора. Увеличение скорости ветра приводит к уменьшению
раствора конуса и смещению его оси к линии, соединяющей центры звезд.
Уменьшение скорости
ветра приводит к заметному усложнению картины течения, и, в частности, к
формированию сложной структуры из ударных волн и тангенциальных разрывов. В
подобных системах при уменьшении скорости ветра наряду с прямым потоком
вещества от звезды-донора существенную
роль начинает играть поток, обусловленный орбитальным движением
звезды-аккретора в газе звездного ветра. Характерная особенность рассчитанной
структуры при малых скоростях ветра (типичных для симбиотических звезд с ![]() < 30-50 км/с и значением
параметра W< 1-1.5) - наличие двух отошедших
ударных волн: одна находится перед аккретором на пути орбитального движения,
другая - между компонентами системы (вместо конической ударной волны). В
системах со слабым ветром вещество, падающее на компактный объект, движется по
закручивающейся спирали, причем скорость его существенно превышает скорость вещества,
не вовлеченного в процесс аккреции.
< 30-50 км/с и значением
параметра W< 1-1.5) - наличие двух отошедших
ударных волн: одна находится перед аккретором на пути орбитального движения,
другая - между компонентами системы (вместо конической ударной волны). В
системах со слабым ветром вещество, падающее на компактный объект, движется по
закручивающейся спирали, причем скорость его существенно превышает скорость вещества,
не вовлеченного в процесс аккреции.
Во всех низкоскоростных (W < 1) вариантах наблюдалось формирование устойчивого аккреционного диска. Напротив, при высоких граничных значениях скорости (W > 1) диск образовывался квазипериодически, лишь в определенные моменты времени, причем при следующем возникновении диска направление движения газа в нем изменялось на противоположное. Оказалось также, что увеличение скорости ветра приводит к существенному уменьшению скорости аккреции, выраженной в долях от темпа истечения вещества от первичного компонента.
Решение задачи о газодинамике массопереноса во взаимодействующих двойных системах все еще далеко от завершения, поскольку многообразие протекающих в системе процессов и сложность их численного моделирования пока не позволяют разработать единую модель, детально описывающую все рассматриваемые системы. [3]
2.4. Эволюция одиночной звезды
Самое долгое время
своей жизни звезда проводит на стадии, определяемой процессами термоядерного
горения водорода в ее недрах. Время пребывания на главной последовательности
диаграммы Герцшпрунга – Рессела очень сильно зависит от массы звезды: чем она
массивнее, тем горячее ее центральные части, но тем скорее израсходуется водородное
топливо в ядре звезды. Так, звезды с массой порядка солнечной находятся на
главной последовательности несколько миллиардов лет. После того, как водород
кончается в ядре, он начинает гореть в узком слое. При этом одиночная звезда
становится очень больших размеров (100–1000 ![]() ),
переходя в класс красных сверхгигантов. Звезды с массой меньше 0,8
),
переходя в класс красных сверхгигантов. Звезды с массой меньше 0,8 ![]() ,
,
 |
вообще не успевают проэволюционировать от стадии главной последовательности за космологическое время (10–13 млрд. лет). [1]
Век массивных звезд
сравнительно короток по космологическим меркам: звезда с массой больше 10![]() на главной последовательности
пребывает не дольше 10 млн. лет. После полного исчерпания водорода загорается
накопившийся в недрах гелий, потом углерод и далее во все убыстряющемся темпе более
тяжелые элементы.
на главной последовательности
пребывает не дольше 10 млн. лет. После полного исчерпания водорода загорается
накопившийся в недрах гелий, потом углерод и далее во все убыстряющемся темпе более
тяжелые элементы.
При этом продукты горения каждой предыдущей реакции становятся топливом для последующей: водород ® гелий ® углерод ®...® железо. В некоторый критический момент, когда в недрах звезды накопится достаточно тяжелых элементов, она теряет свою устойчивость и ее ядро коллапсирует под действием сил гравитации. В процессе коллапса высвобождается гигантская энергия (~1052 эрг) – происходит грандиозная вспышка сверхновой.
В среднем в нашей
Галактике одна сверхновая вспыхивает примерно раз в несколько сотен лет. На
месте сверхновой может остаться компактный объект – нейтронная звезда или
черная дыра. Массы нейтронных звезд не превосходят 3![]() , а их радиусы – около 10
км. Черные дыры могут иметь любые звездные массы.
, а их радиусы – около 10
км. Черные дыры могут иметь любые звездные массы.
Если начальная масса
звезды меньше 10![]() , то
эволюция протекает иначе. На стадии красного гиганта у нее формируется
вырожденное гелиевое или углеродно-кислородное
ядро, которое после сброса внешней оболочки (при этом образуется планетарная
туманность) превращается в белый карлик – звезду, где гравитационным силам
сжатия противостоит давление вырожденного электронного газа.
, то
эволюция протекает иначе. На стадии красного гиганта у нее формируется
вырожденное гелиевое или углеродно-кислородное
ядро, которое после сброса внешней оболочки (при этом образуется планетарная
туманность) превращается в белый карлик – звезду, где гравитационным силам
сжатия противостоит давление вырожденного электронного газа.
2.5. Особенности эволюции звезд в паре
Эволюцию двойных
систем принято делить на два типа: эволюцию массивных систем, в которых хотя бы
одна из компонент имеет массу ³10![]() , и эволюцию систем малых и
умеренных масс. У систем первого типа закономерным следствием эволюции является
вспышка сверхновой звезды, у вторых – вспышка сверхновой возможна лишь при
очень специфических условиях: когда на белый карлик, образовавшийся в ходе
обычной эволюции одной из компонент, «натекает» вещество со второй звезды. Белый карлик наращивает
свою массу вплоть до того момента, когда уже вырожденный релятивистский электронный
газ не в состоянии противостоять гравитационному сжатию. Этот фундаментальный
предел массы (1,4
, и эволюцию систем малых и
умеренных масс. У систем первого типа закономерным следствием эволюции является
вспышка сверхновой звезды, у вторых – вспышка сверхновой возможна лишь при
очень специфических условиях: когда на белый карлик, образовавшийся в ходе
обычной эволюции одной из компонент, «натекает» вещество со второй звезды. Белый карлик наращивает
свою массу вплоть до того момента, когда уже вырожденный релятивистский электронный
газ не в состоянии противостоять гравитационному сжатию. Этот фундаментальный
предел массы (1,4![]() ) был открыт в 30-х годах нашего века С. Чандрасекаром и
носит его имя. [15]
) был открыт в 30-х годах нашего века С. Чандрасекаром и
носит его имя. [15]
Рассмотрим, как меняется орбита системы в процессе обмена веществом. Во многих случаях обмен масс в двойной системе с большой точностью можно считать консервативным, то есть все вещество, истекающее с одной звезды, полностью перехватывается соседней и орбитальный момент системы не изменяется. Из условия сохранения момента следует, что при перетекании вещества с более массивной компоненты на менее массивную расстояние между звездами должно уменьшаться. В противном случае – когда вещество истекает с менее массивной компоненты – расстояние между ними должно увеличиваться.
По ряду причин вещество может не полностью перехватываться соседней компонентой и часть его покидает систему, унося угловой момент. Тогда процесс перетекания неконсервативен, угловой момент не сохраняется, В этом случае расчет эволюции усложняется. По общей теории относительности (ОТО) орбитальный момент импульса двойной системы должен всегда убывать, вне зависимости от того, происходит в системе перетекание вещества или нет.
Глава 3. Уникальный объект SS 433
3.1. Загадка SS 433
Об этом удивительном небесном объекте написано уже немало. Речь идет об источнике в созвездии Орла, занесенном в каталог ярких эмиссионных звезд Ц. Стефенсона и Н. Сандулека под номером 433. SS 433 – уникальная по своим свойствам тесная двойная система: несмотря на тщательные поиски, других подобных источников пока в Галактике не обнаружено. Источник удивителен по богатству ярких феноменов, физика которых во многом до настоящего времени окончательно не выяснена. [9]
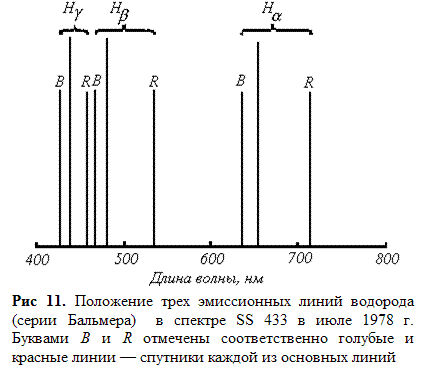 |
Внимание к себе он привлек после того, как английскими учеными Д. Кларком и П. Мардиным была получена первая спектрограмма с высоким разрешением в оптическом диапазоне. В 1977 г. Б. Стефенсон и Н. Сандулек опубликовали список звезд, замечательных тем, что в их спектрах имелись яркие эмиссионные линии. Дальнейшее изучение показало, что одна из этих звезд невидимая простым глазом звезда под номером SS 433 в районе созвездия Орла вблизи центральной плоскости Галактики, выделяется необычайным обилием эмиссионных линий. В ее спектре имеются яркие эмиссионные линии водорода, гелия, некоторых других элементов. Но около каждой из этих линий находится по две дополнительные эмиссионные линии несколько меньшей интенсивности – одна слева, а другая справа.
Это особенно четко видно в линиях атома водорода (серии Бальмера) – самых сильных из всех эмиссионных линий SS 433 – см. рис. 11. На рисунке дополнительные линии, лежащие слева от основной, т е. в сторону голубого края спектра, отмечены буквой В от слова blue – голубой; будем называть их голубыми линиями-спутниками. Дополнительные линии, лежащие справа от основной, т. е. в сторону красного края спектра, отмечены буквой R – от слова red – красный, будем называть их красными линиями-спутниками. Можно заметить, что линии-спутники расположены относительно основных в строгом порядке. Именно на шкале длин волн каждая голубая линия-спутник отстоит от основной на отрезок, который пропорционален длине волны основной линии:
![]() (3.1)
(3.1)
Здесь ![]() - разность длин волн голубой линии-спутника и основной
линии; индекс «i» пробегает значения
- разность длин волн голубой линии-спутника и основной
линии; индекс «i» пробегает значения ![]() , которыми различаются линии
в спектральной серии, так что приведенное соотношение содержит столько
уравнений, сколько имеется основных линий (на рис. 11. показаны три основных
линии); коэффициент пропорциональности
, которыми различаются линии
в спектральной серии, так что приведенное соотношение содержит столько
уравнений, сколько имеется основных линий (на рис. 11. показаны три основных
линии); коэффициент пропорциональности ![]() одинаков и отрицателен по знаку для
всех голубых линий-спутников.
одинаков и отрицателен по знаку для
всех голубых линий-спутников.
То же и с красными линиями-спутниками:
![]() (3.2)
(3.2)
Здесь столько
уравнений, сколько значений пробегает индекс «i»; значение ![]() одинаково
для всех красных линий-спутников и положительно по знаку; по абсолютной
величине
одинаково
для всех красных линий-спутников и положительно по знаку; по абсолютной
величине ![]() и
и ![]() не совпадают между собой:
не совпадают между собой: ![]() >
>![]() .
.
Фактически в спектре SS 433 имеются три системы спектральных линий: одна система на своем стандартном месте на шкале длин волн – это система основных линий – и две другие системы линий, смещенные относительно стандартного положения в голубую и красную стороны. Это смещение представляет собой не просто сдвиг линий с сохранением их относительных положений (т. е. расстояний между ними на шкале длин волн), а сдвиг с изменением относительных положений, так как, сдвиг каждой дополнительной линии от основной тем больше, чем больше длина волны основной линии.
Смещения спектральных линий сами по себе не новость в астрономии. Более полувека назад пулковский астроном А. А. Белопольский наблюдал смещение линий в спектрах звезд и по величине и знаку смещения определял лучевые скорости звезд, т. е. скорости вдоль луча зрения. Смещение линий от их стандартного положения служат для астрономов безошибочным указанием на то, что источник излучения движется относительно наблюдателя. Изменение длин волн и частот излучаемого света, вызываемое относительным движением источника и приемника света, носит название эффекта Доплера. [22]
Эффект Доплера
Эффект Доплера возможен при любом волновом или периодическом движении. Он знаком всем по примеру с поездом, когда гудок поезда кажется более высоким по тону при приближении поезда и низким – при удалении. Воспринимаемая ухом частота звуковых волн больше при приближении и меньше при удалении источника звука. То же и с электромагнитными волнами. Хотя полной аналогии и нет. Дело в том, что звуковые волны распространяются только в среде, а электромагнитные волны могут распространяться и в пустоте. Поэтому в акустике различают движения источника и приемника звука относительно среды, а для электромагнитной волны существенно лишь относительное движение источника и приемника, т. е. только изменение расстояния между ними. Кроме того, электромагнитные волны распространяются в пустоте с максимально возможной скоростью, со скоростью света с, тогда как скорость звука определяется свойствами среды, по которой он распространяется. Покажем, как можно получить формулы, описывающие эффект Доплера для света. Допустим, имеется источник, который посылает нам короткие импульсы, вспышки света. Эти импульсы регистрируются приемником света, и мы
 |
будем фиксировать моменты испускания и прихода импульсов.
Пусть один
импульс испущен в момент ![]() и
достиг нас в момент
и
достиг нас в момент ![]() , а следующий за
ним испущен в момент
, а следующий за
ним испущен в момент ![]() и принят в момент
и принят в момент
![]() . В первом случае
свет распространялся в течение времени
. В первом случае
свет распространялся в течение времени ![]() и
прошел путь
и
прошел путь ![]() ; во втором случае время распространения
; во втором случае время распространения ![]() и
путь
и
путь ![]() . Если источник, покоится относительно нас и расстояние до
него не меняется, то, очевидно, оба пути света равны. Если же источник
движется, то пути различны: приближение источника сокращает путь света, а удаление
увеличивает.
. Если источник, покоится относительно нас и расстояние до
него не меняется, то, очевидно, оба пути света равны. Если же источник
движется, то пути различны: приближение источника сокращает путь света, а удаление
увеличивает.
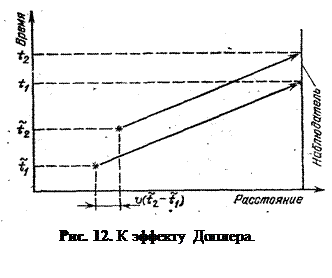
Рассмотрим
сначала случай приближающегося источника (рис. 12). Если он движется по
направлению к нам со скоростью ![]() , то вторая вспышка будет испущена в
точке, которая на отрезок пути
, то вторая вспышка будет испущена в
точке, которая на отрезок пути ![]() ближе:
ближе:
![]() -
-![]() =
=![]() (3.3)
(3.3)
Перепишем это уравнение в несколько ином виде:
![]() (3.4)
(3.4)
Представим
себе теперь, что мы следим не за отдельными вспышками, а за непрерывно
испускаемыми волнами. Тогда мы можем выбрать моменты испускания ![]() и
и ![]() так, чтобы
промежуток времени между ними равнялся периоду испускаемой волны
так, чтобы
промежуток времени между ними равнялся периоду испускаемой волны ![]() :
:![]() =
=![]() . А период принимаемой волны T выразится через t1 и t2:
. А период принимаемой волны T выразится через t1 и t2: ![]() =T
=T
Тогда из уравнения (3.4) получаем
следующую связь между T и ![]()
![]() (3.5)
(3.5)
Мы видим, что принимаемый период меньше периода испущенной волны.
Если источник
не приближается, а удаляется, в последней формуле нужно, очевидно, изменить
знак перед скоростью на обратный. Это дает возрастание периода колебаний. При
произвольной ориентации движения источника скорость ![]() в
последнем соотношении нужно, как легко видеть, заменить произведением
в
последнем соотношении нужно, как легко видеть, заменить произведением ![]() , где
, где ![]() – угол между направлением движения источника и направлением
распространения волны (т. е. лучом зрения):
– угол между направлением движения источника и направлением
распространения волны (т. е. лучом зрения):
![]() (3.6)
(3.6)
Под величиной
![]() здесь нужно понимать
абсолютную величину вектора скорости, a
здесь нужно понимать
абсолютную величину вектора скорости, a
![]() -
-![]() лучевая
скорость, т. е. проекция скорости на луч зрения.
лучевая
скорость, т. е. проекция скорости на луч зрения.
Полученная
формула (3.6) довольно проста, но в действительности она имеет столь простой
смысл лишь тогда, когда скорость движения источника очень мала по сравнению со
скоростью света: ![]() . Если это условие не выполнено, в игру
вступают новые физические явления, релятивистские эффекты, в которых
проявляются свойства относительности времени и пространства, изучаемые теорией
относительности. Очень важно, что при больших скоростях, сравнимых со скоростью
света (а именно с этим случаем мы и встретимся в источнике SS 433), показания движущихся и покоящихся
часов не совпадают.
. Если это условие не выполнено, в игру
вступают новые физические явления, релятивистские эффекты, в которых
проявляются свойства относительности времени и пространства, изучаемые теорией
относительности. Очень важно, что при больших скоростях, сравнимых со скоростью
света (а именно с этим случаем мы и встретимся в источнике SS 433), показания движущихся и покоящихся
часов не совпадают.
В
рассуждениях, приведших к формуле (3.6) подразумевалось, что регистрация
моментов времени производится по часам астронома-наблюдателя, который принимает
излучение, приходящее к нему от движущегося источника света. По этим часам был
измерен период принимаемой волны T. По тем же часам измерялся и период
испущенной волны ![]() . Но между этими двумя измерениями имеется существенная
разница. Одно измерение производилось там, где происходило интересующее нас
событие: приход света регистрировался по часам, находящимся тут же у приемника.
Другое же измерение производилось вдали от места, где происходило событие:
моменты испускания света регистрировались по часам, находящимся не у источника,
а у приемника. Величина
. Но между этими двумя измерениями имеется существенная
разница. Одно измерение производилось там, где происходило интересующее нас
событие: приход света регистрировался по часам, находящимся тут же у приемника.
Другое же измерение производилось вдали от места, где происходило событие:
моменты испускания света регистрировались по часам, находящимся не у источника,
а у приемника. Величина ![]() – это период испущенной волны, измеренный по часам приемника.
– это период испущенной волны, измеренный по часам приемника.
Какой период
испущенной волны показали бы часы, находящиеся на самом источнике? Согласно
теории относительности движущиеся часы всегда идут медленнее неподвижных;
промежуток времени между какими-то двумя событиями, измеренный движущимися
часами, будет в отношении «релятивистского корня» ![]() меньше, чем промежуток времени между теми же событиями,
измеренный по покоящимся часам. Поэтому часы, движущиеся вместе с источником
света, покажут меньший период испущенной волны, чем часы покоящегося
наблюдателя
меньше, чем промежуток времени между теми же событиями,
измеренный по покоящимся часам. Поэтому часы, движущиеся вместе с источником
света, покажут меньший период испущенной волны, чем часы покоящегося
наблюдателя
![]() (3.7)
(3.7)
T0 – это и - есть период испущенной волны, измеренный по часам источника.
Время, отсчитываемое по часам, движущимся вместе с данным телом, называется собственным временем этого тела. Промежуток собственного времени движущегося тела всегда короче соответствующих промежутков времени, измeренных по неподвижным часам.
Пользуясь релятивистской формулой (3.7), можно, наконец, записать окончательную формулу эффекта Доплера, в которой период принимаемых волн T выражен через собственный период T0 источника:
 (3.8)
(3.8)
От периода
легко перейти к длине волны ![]() и
частоте
и
частоте ![]() колебаний:
колебаний:
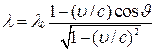 (3.9)
(3.9)
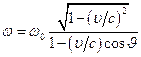 (3.10)
(3.10)
Здесь ![]() и
и
![]() – длина волны и
частота света, измеренные по собственным часам источника. Когда в лаборатории
измеряется период колебательного процесса, то дли этого используются
лабораторные часы, показывающие, очевидно, собственное время источника колебаний,
находящегося тут же. Поэтому измеряемый в лаборатории период – это период
собственного времени источника. И когда выше мы говорили о частотах и длинах
волн испускаемого атомами света, мы, естественно, имели в виду лабораторные
величины, т. е. величины, измеренные в собственном времени. Им отвечают
«стандартные» положения линий в спектре источника.
– длина волны и
частота света, измеренные по собственным часам источника. Когда в лаборатории
измеряется период колебательного процесса, то дли этого используются
лабораторные часы, показывающие, очевидно, собственное время источника колебаний,
находящегося тут же. Поэтому измеряемый в лаборатории период – это период
собственного времени источника. И когда выше мы говорили о частотах и длинах
волн испускаемого атомами света, мы, естественно, имели в виду лабораторные
величины, т. е. величины, измеренные в собственном времени. Им отвечают
«стандартные» положения линий в спектре источника.
Из формулы
(3.9) видно, что длина волны в излучении движущегося источника возрастает и,
следовательно, линия в спектре смещается к его красному концу, как благодаря
удалению источника, так и из-за релятивистского эффекта замедления времени.
Уменьшение длины волны и сдвиг линии в более голубую область спектра связаны с
приближением источника, но результат ослабляется из-за замедления времени;
можно видеть, что замедление, времени способно даже полностью ликвидировать
эффект приближения при определенном соотношении между скоростью ![]() и углом
и углом ![]() . [20, 14]
. [20, 14]
Смещение
линий в спектрах характеризуют уже знакомой нам величиной ![]() , называемой, как это
принято, красным смещением (
, называемой, как это
принято, красным смещением (![]() – стандартная длина волны,
– стандартная длина волны, ![]() – смещенная длина волны). Смещение действительно является
красным, когда величина z
положительна. Когда величина z отрицательна,
это означает сдвиг в голубую часть спектра. Таким образом, на основании можно
написать
– смещенная длина волны). Смещение действительно является
красным, когда величина z
положительна. Когда величина z отрицательна,
это означает сдвиг в голубую часть спектра. Таким образом, на основании можно
написать
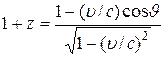 (3.11)
(3.11)
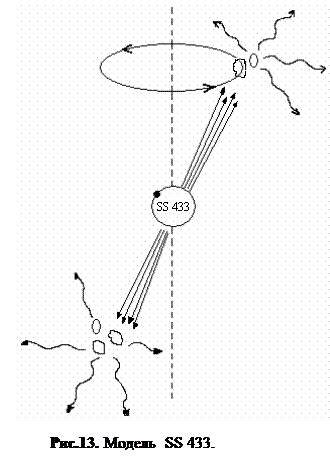
В спектре объекта SS 433 (V 1343 Орла) наблюдаются три системы спектральных линий, принадлежащих бальмеровской серии водорода: две системы движутся по спектру в противофазе с периодом ~ 164 дня и амплитудой до ~ 1000Ǻ, а третья система линий неподвижна. Установлено, что движущиеся эмиссионные линии возникают в двух противоположно направленных струях или выбросах (см. рис), направление которых меняются с периодом 164 дня. На одной из спектограмм длина волны линии Hα смещенной в красную сторону, оказалась равной 7730Ǻ, а смещенной в синюю сторону - 6160Ǻ. Определим скорость выброшенного вещества. [13]
![]() Обычную формулу эффекта
Доплера
Обычную формулу эффекта
Доплера ![]() при очень больших скоростях
надо заменить более сложной, вытекающей из специальной теорией относительности
Эйнштейна:
при очень больших скоростях
надо заменить более сложной, вытекающей из специальной теорией относительности
Эйнштейна:
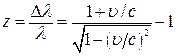 , (3.12)
, (3.12)
z – красное смещение.
Выразив скорость из выражения (3.12), получим:
![]() . (3.13)
. (3.13)
Эта формула удовлетворяет принципу, по которому никакая скорость в природе не может превысить некоторой предельной, с которой свет распространяется в вакууме (30000 м/с). [11]
![]() . (3.14)
. (3.14)
 |
Линия водорода серии Бальмера Hα - 6563 Ǻ. [7]
Так как длина волны линии Hα смещенной в красную сторону, оказалась равной 7730Ǻ, то значение для красного смещения z получим равным –0,178. То, что величина z отрицательна, это означает смещение линий в голубую часть спектра. А при длине волны смещенной в синюю сторону - 6160Ǻ, z=0,061 и смещена в красную часть спектра. Вследствие эффекта Доплера в первом случае выбросы будут удаляться от нас, во втором случае приближаться к нам. Это говорит, что выбросы на самом деле движутся в противоположных направлениях. Подставляя значения z в формулу (3.13), получим, что выбросы удаляются от нас и приближаются к нам со скоростями:
 .
.
![]() =-57995 км/с знак «
- » еще раз доказывает, что объект движется от нас, далее его мы не будем
учитывать.
=-57995 км/с знак «
- » еще раз доказывает, что объект движется от нас, далее его мы не будем
учитывать.
Скорость выброшенного вещества для данных смещенных линий в спектре равна сумме полученных скоростей:
![]() =
= ![]() +
+ ![]() = 57995 + 17779 = 75774
км/с.
= 57995 + 17779 = 75774
км/с.
Движущиеся линии
Тот факт, что в спектре SS 433 имеются три системы спектральных линий, означает, что в нем имеются, и три излучающие области: одна из них не движется относительно нас, а две другие движутся в разные стороны вдоль луча зрения. Чтобы получить представление о скоростях этих движений, воспользуемся данными, которые астрономы получили в наблюдениях лета 1978 г., когда началось изучение источника SS 433.
Измеренные тогда значения zВ и zr составляли: zB=-0.02, zR=0.l.
На основании формулы эффекта Доплера (3.11), находим для приближающейся к нам области
 (3.15)
(3.15)
Это соотношение
содержит две неизвестные величины – полную скорость движения области ![]() и ее проекцию на луч зрения
и ее проекцию на луч зрения ![]() . Если допустить, что отношение
. Если допустить, что отношение ![]() мало по сравнению с единицей, то лучевая скорость
мало по сравнению с единицей, то лучевая скорость ![]() =0;02 с=6000 км/с.
=0;02 с=6000 км/с.
Это довольно
большая скорость, если сравнить ее со скоростями движения звезд в Галактике;
последние не превышают нескольких сотен километров в секунду. В пределах 100 –
300 км/с лежат лучевые скорости звезд, найденные А. А. Белопольским, а за ним и
другими наблюдателями. Для движения звезд пренебрежение величиной ![]() в знаменателе формулы эффекта Доплера вполне оправдано. В
случае SS 433 речь явно идет о гораздо более быстром
движении излучающей области, чем обычные движения звезд Галактики, Этим и
полезна оценка лучевой скорости; но даваемое ею конкретное значение лучевой
скорости следует все же принимать с осторожностью. В нашем распоряжении нет никаких
независимых данных об угле
в знаменателе формулы эффекта Доплера вполне оправдано. В
случае SS 433 речь явно идет о гораздо более быстром
движении излучающей области, чем обычные движения звезд Галактики, Этим и
полезна оценка лучевой скорости; но даваемое ею конкретное значение лучевой
скорости следует все же принимать с осторожностью. В нашем распоряжении нет никаких
независимых данных об угле ![]() , и строгим единственным результатом
должно считаться соотношение (3.15), связывающее этот угол со скоростью
, и строгим единственным результатом
должно считаться соотношение (3.15), связывающее этот угол со скоростью ![]()
Для удаляющейся от нас области излучения имеем
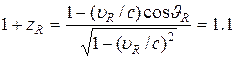 (3.16)
(3.16)
В том же
предположении ![]() <<l находим лучевую скорость
<<l находим лучевую скорость ![]() =-0,1 с=-30000 км/с. Лучевая скорость
отрицательна, что и соответствует удалению источника, так как в этом случае
=-0,1 с=-30000 км/с. Лучевая скорость
отрицательна, что и соответствует удалению источника, так как в этом случае ![]() <0. Эта скорость в 100 раз больше (по абсолютной величине)
типичной скорости звезд в Галактике ~300 км/с, что подтверждает указание на
особый, не звездный характер движения излучающих областей SS 433. Значения обеих лучевых скоростей
<0. Эта скорость в 100 раз больше (по абсолютной величине)
типичной скорости звезд в Галактике ~300 км/с, что подтверждает указание на
особый, не звездный характер движения излучающих областей SS 433. Значения обеих лучевых скоростей ![]() и
и ![]() будут получены ниже.
будут получены ниже.
Ни в Галактике, ни вне ее никогда не наблюдалось прежде источника, который излучал бы сразу две системы линий, столь сильно сдвинутых от стандартных положений. Большие смещения в красную сторону спектра встречаются у квазаров, самых далеких объектов Вселенной. Во всех же известных до сих пор случаях смещения в голубую сторону абсолютное значение z меньше, по крайней мере, в 20-100 раз, чем у SS 433.
 |
Но самое удивительное было обнаружено в наблюдениях осени 1978 – весны 1979 гг. Американский астроном Б. Маргон и его сотрудники, наблюдая SS 433 в сентябре 1978 г., нашли эмиссионные линии-спутники на иных местах, чем за два месяца до того: они разъехались в разные стороны. Значения |zB| и zR возросли и продолжали затем возрастать до ноября 1978 г., пока не достигли максимальных значений |zB|max=0,l; (zR)mах=0,18. Затем началось уменьшение |zB| и zR, и в течение декабря, пока продолжались наблюдения, линии-спутники приближались к основным линиям спектра. Когда в марте 1979 г. наблюдения были продолжены (с декабря до февраля источник не виден), оказалось, что линии-спутники снова удаляются от основных линий; в конце апреля был достигнут новый максимум, причем |zB| и zR вновь приняли те же значения, что при первом максимуме.
Дальнейшие наблюдения (вплоть до последних данных, ставших известными к лету 1982 г.) подтвердили, что изменения смещений линий-спутников происходят с регулярной периодичностью. Все наблюдательные данные очень хорошо ложатся на две одинаковые по форме периодические кривые, сдвинутые друг относительно друга так, что максимуму одной отвечает минимум другой и наоборот (рис. 14). Период изменения смещений – 164 дня.[12]
Кроме момента максимальных значений |zB| и zR (он отмечен на рис. 14 буквой, а), имеются еще три других выделенных момента (отмеченных буквами b, с, d) на рис. 14. В момент b кривые пересекаются, величина красного смещения для обеих кривых одинакова и положительна по знаку: zB=0,04. В момент с достигаются значения (zB)c=-0.01 (zR)c=0,09. В момент d имеется второе за период пересечение кривых с тем же значением z, что и в момент b.
В каждый из моментов а, b, с, d сумма красных смещений по обеим кривым одинакова: zB+zR =0,08. Равенство суммы красных смещений имеется вообще в любой момент времени.
Понимая смещение линий в спектре источника как следствие движения двух излучающих областей, каждой из которых отвечает своя кривая на рис. 14, мы должны теперь считать, что это движение имеет периодический характер. Каждая из излучающих областей то приближается к нам, то удаляется от нас, и когда одна приближается, другая удаляется, и наоборот. Дважды за период области меняются местами: та, что приближалась, начинает удаляться, а та что удалялась, начинает приближаться. В эти моменты (b и d на рис. 14) лучевые скорости излучающих областей должны, очевидно, обращаться в нуль.
То
обстоятельство, что при обращении в нуль лучевых скоростей красное смещение
остается отличным от нуля, указывает на важность релятивистского эффекта
замедления времени; он учитывается корнем в формулах эффекта Доплера. Для
момента b, когда лучевая скорость ![]() =0, находим значение полной скорости, соответствующее
красному смещению zb=0,04:
=0, находим значение полной скорости, соответствующее
красному смещению zb=0,04:
![]() (3.17)
(3.17)
Это весьма значительная скорость, и ее значение характеризует обе излучающие области – факт, который имеет немалое значение для понимания всей картины.
Прецессия струй
Остроумную интерпретацию кинематики излучающих областей SS 433 предложили английские астрофизики А. Фабиан и М. Рис. Согласно их идее в источнике имеется центральное тело, из которого истекают в противоположных направлениях две струи газа. С центральным телом связана основная излучающая область, которая дает несмещенные спектральные линии, а струи – это области, из которых исходят смещенные линии излучения.
Далее, направление, вдоль которого выбрасываются струи, не остается неизменным во времени. Линия струй совершает обращение вокруг некоторой оси. Движение линии струй похоже на вращение оси волчка, запущенного так, что эта ось не вертикальна: ось волчка медленно (медленнее, чем вращение волчка) вращается вокруг вертикали. Такое периодическое движение оси волчка (или гироскопа) называют прецессией.
Эта модель способна полностью воспроизвести кривые красного смещения на рис. 14. Нужно только должным образом подобрать скорости струй, ориентацию оси прецессии относительно земного наблюдателя и угол, который струи составляют с осью прецессии (рис.15)
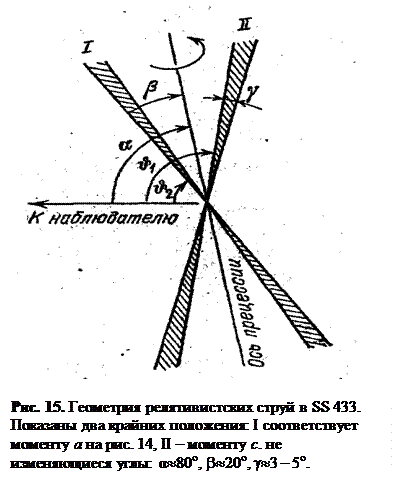 |
В самом деле, когда в движении одной из струй имеется составляющая вдоль луча зрения, направленная к нам, в движении другой струи будет составляющая, направленная по лучу зрения от нас. Это дает соответственно голубую и красную системы линий-спутников.
Из-за прецессии струй их ориентация относительно наблюдателя изменяется; периодически во времени изменяется угол, который линия струй составляет с лучом зрения. Вместе с этим углом периодически изменяются и лучевые скорости струй. Ничто не мешает выбрать период прецессии равным наблюдаемому, т. е. 164 дням.
Из того, что сумма красных смещений обеих областей всегда одна и та же следует, что лучевые скорости струй в каждый момент времени равны по величине и противоположно направлены. Это возможно, очевидно, лишь в том случае, если абсолютные величины скорости обеих струй равны.
Допустимо
такое положение струй, при котором они перпендикулярны лучу зрения. В такие
моменты (моменты b и d на рис. 14), лучевые скорости обращаются в нуль. Вычисленная ранее
по данным об этих моментах скорость -![]() (см.
(3.11)) является скоростью движения вещества в струях и она одинакова
для обеих струй. Теперь становится ясным смысл результата (3.11): величина
(см.
(3.11)) является скоростью движения вещества в струях и она одинакова
для обеих струй. Теперь становится ясным смысл результата (3.11): величина ![]() характеризует сразу
обе излучающие области, потому что скорость выброса обеих струй одинакова.
характеризует сразу
обе излучающие области, потому что скорость выброса обеих струй одинакова.
Скорость ![]() составляет
приблизительно одну четвертую часть скорости света. Это очень большая скорость,
и потому сделанные нами предварительные оценки лучевых; скоростей (относящиеся
к тому состоянию источника, которое наблюдалось летом 1978 г.) должны быть
уточнены. С учетом релятивистского корня
составляет
приблизительно одну четвертую часть скорости света. Это очень большая скорость,
и потому сделанные нами предварительные оценки лучевых; скоростей (относящиеся
к тому состоянию источника, которое наблюдалось летом 1978 г.) должны быть
уточнены. С учетом релятивистского корня ![]() лучевые скорости оказываются одинаковыми
по абсолютной величине:
лучевые скорости оказываются одинаковыми
по абсолютной величине: ![]() =
=![]() ==0,06с.
==0,06с.
Двойная система
Модель прецессирующих струй дает простой и красивый ответ на вопрос, как в одном источнике могут возникнуть три системы эмиссионных линий с их запутанными, на первый взгляд, изменениями во времени. Гораздо труднее ответить на вопрос, почему возникают и прецессируют струи, бьющие со скоростями, близкими к скорости света. Тщательные наблюдения и углубленный анализ данных позволят, как можно надеяться, приблизиться к пониманию физического механизма действующего источника SS 433. Накопление сведений продолжается, и ряд важных обстоятельств уже удалось выяснить.
Прежде всего, можно сделать определенное заключение о температуре газа в излучающих областях SS 433. Для водорода, эмиссионные спектры которого сильнее всех других линий в этом источнике, имеется характерная температура порядка 10 тысяч градусов; она определяет границу между ионизованным и не ионизованным состояниями газа. Если температура превышает 10 – 20 тысяч градусов, тепловые движения атомов столь энергичны, что при их столкновениях электронам может быть передана энергия, превышающая максимально возможную энергию электрона в атоме и, следовательно, достаточная для отрыва электронов от ядер. В таком состоянии имеются, свободные электроны и свободные ядра водорода – протоны, газ ионизован и представляет собой плазму. Когда электроны не связаны с ядрами в атомы, спектральные линии, соответствующие переходам электронов в атомах, возникать, очевидно, не могут. Так как в SS 433 линии наблюдаются, температура излучающих областей не превышает характерной температуры ионизации и 20 тысяч градусов – это для нее верхний предел.
Температура вещества в струях не может быть и слишком низкой – ведь совсем холодный газ линии не излучает. Скорее всего, температура излучающих областей SS 433 близка к 10 тысячам градусов. Средние скорости тепловых движений атомов при такой температуре, можно найти по общей формуле - кинетической теории газов;
![]() (3.18)
(3.18)
Здесь k=1,38·10-23Дж/К – постоянная
Больцмана, mн=1,67·10-27 кг -масса атома водорода. При T=104
К ![]() =2 ·104
м/с=20 км/с. Эта скорость в 4 тысячи раз меньше скорости движения струй. Такое
значительное различие скоростей само по себе требует объяснения.
=2 ·104
м/с=20 км/с. Эта скорость в 4 тысячи раз меньше скорости движения струй. Такое
значительное различие скоростей само по себе требует объяснения.
Интересны
соображения о собственной ширине струй. Струи не могут быть слишком широкими:
будь их угол раствора ![]() сравним с углом
прецессии
сравним с углом
прецессии ![]() 20°, вся картина была бы
смазанной и нечеткой. Вместо линий в спектре источника имелись бы размытые
полосы, соответствующее всем различным значениям лучевой скорости, которые она
принимает на толщине струи. В действительности линии-спутники в SS 433 весьма узки, и в крайних положениях
их толщина во всяком случае гораздо меньше расстояния до основной линии на
шкале длин волн. По-видимому, угол раствора
20°, вся картина была бы
смазанной и нечеткой. Вместо линий в спектре источника имелись бы размытые
полосы, соответствующее всем различным значениям лучевой скорости, которые она
принимает на толщине струи. В действительности линии-спутники в SS 433 весьма узки, и в крайних положениях
их толщина во всяком случае гораздо меньше расстояния до основной линии на
шкале длин волн. По-видимому, угол раствора ![]() не
больше 3-4°. Столь высокая степень направленности струй представляет собой, пожалуй,
один из самых трудных вопросов в физике SS 433.
не
больше 3-4°. Столь высокая степень направленности струй представляет собой, пожалуй,
один из самых трудных вопросов в физике SS 433.
Внимательное изучение основной излучающей области SS 433 обнаружило, что излучаемые ею линии не стоят на месте: они тоже совершают периодические смещения по шкале длин волн, но только гораздо более слабые, чем линии-спутники (потому-то эти движения и не сразу заметили). Эти слабые смещения соответствуют периодическим движениям с амплитудой (максимальным значением абсолютной величины) скорости около 70 км/с. Это в 1000 раз меньше скорости струй. Период слабых смещений равен 13 дням.
Период и скорость, соответствующие слабым смещениям эмиссионных линий из основной излучающей области, очень близки к тому, что обычно наблюдается в тесных двойных системах звезд. Довольно естественно понимать эти данные так, что в SS 433 имеются две звезды, совершающие периодические – с периодом 13 дней – движения вокруг их общего центра масс. Тогда традиционные методы астрономии, разработанные и испытанные в многочисленных наблюдениях двойных звезд, должны и здесь многое прояснить.
Действительно,
детальные оптические наблюдения позволяют утверждать, что одна из звезд в SS 433 – обычная звезда спектрального класса
О или В с массой в (10 – 20) ![]() ,
температурой поверхности 20 тысяч градусов и радиусом в 2·10l9 м. С радиусом этой звезды сравним и размер двойной системы,
т. е. расстояние между ее компонентами.
,
температурой поверхности 20 тысяч градусов и радиусом в 2·10l9 м. С радиусом этой звезды сравним и размер двойной системы,
т. е. расстояние между ее компонентами.
Соображения, которыми обычно пользуются астрономы для определения расстояний до звезд (они связаны в первую очередь с интенсивностью линий поглощения, создаваемых в спектре источника межзвездным газом), позволили оценить и удалённость SS 433: источник находится до нас на расстоянии приблизительно в 5,5 кпк. Это гораздо больше расстояния до ближайших к нам звезд (несколько парсек), но все же заметно меньше поперечника Галактики (около 30 кпк).
Зная расстояние, можно по принимаемому потоку излучения оценить и полную энергию, испускаемую источником в единицу времени (если считать, что он одинаково светит во все стороны). Так найдена полная светимость SS 433: L=1032-1033 Вт, что в сотни тысяч или миллионы раз больше светимости Солнца. На свет струй приходится около одного процента полной светимости. Размеры их излучающих областей оцениваются в 1010м, что сравнимо с размером двойной системы.
SS 433 испускает не только оптическое, но также рентгеновское и радиоизлучение. На рентгеновской карте источника различают центральный источник рентгеновских лучей и протяженные вытянутые структуры с собственными размерами, значительно превышающими размеры двойной звездной системы. Сходное строение обнаруживается и по радиоастрономическим данным. Рентгеновская светимость составляет 3 ·1028 Вт, радиосветимость – 3 ·1025Вт.
Все это очень
напоминает хорошо известную астрономам картину туманностей, которые остаются на
небе от вспышек сверхновых звезд. Скорее всего, что и SS 433, т. е. двойная звезда вместе с протяженными областями,
излучающими рентгеновские лучи и радиоволны, – результат вспышки сверхновой, происшедшей,
насколько можно судить, десятки тысяч лет назад. Но если так, то можно
высказать определенные догадки и о второй звезде, составляющей вместе с обычной
звездой двойную систему SS 433. Она
может быть компактным остатком сверхновой – нейтронной звездой или черной
дырой. Согласно данным советского астронома А. М. Черепащука компактный объект
в SS 433 может иметь массу до (4 – 5) ![]() . При массе, превышающей
предел в (3 – 3,5)
. При массе, превышающей
предел в (3 – 3,5)![]() , это должна быть
черная дыра, а не нейтронная звезда.
, это должна быть
черная дыра, а не нейтронная звезда.
Как и в уже известных тесных двойных систему в SS 433 можно предполагать перетекание вещества с обычной звезды на компактный объект под действием его силы притяжения. Не исключено, что вещество захватывается на круговые орбиты, закручивается вокруг компактного объекта, прежде чем упасть на него, и образует довольно значительный по массе вращающийся диск, похожий по виду на кольца Сатурна. Предполагают, что именно из такого диска – вдоль его оси – и могли бы выбрасываться струи, обнаруженные в SS 433. Их могло бы питать вещество, перетекающее с обычной звезды на комнатный объект.
Что разгоняет вещество струй до релятивистских скоростей? Почему струи такие узкие? Какова причина и прецессии?
Эти важные вопросы ждут своего решения.
Но есть и еще один вопрос, возможно, самый важный и интересный. В явлениях совсем иного, гораздо большего масштаба, в мире гигантских радиогалактик и квазаров, известны выбросы и струи, непосредственно наблюдаемые по их оптическому и радиоизлучению. В некоторых-случаях вещество выбрасывается с явно релятивистскими скоростями. Узкие вытянутые структуры простираются на расстояния в десятки и сотни килопарсек. Не встречаемся ли мы здесь с явлением той же природы, что и в SS 433, но только увеличенным до огромных размеров? Или иначе – не служит ли SS 433 уменьшенной в 1010 – 1012 раз копией огромного «механизма», действующего в активных ядрах галактик и квазарах?
Не исключено, что в обоих случаях причиной релятивистских выбросов и струй служат мощные газодинамические процессы, развивающиеся в окрестности черной дыры.
Понимание этих процессов остается пока далеко не полным; но, замечательна уже и сама возможность универсального физического механизма, действующего в столь различных масштабах, как двойная звезда SS 433 и гигантские радиогалактики и квазары. [21]
3.2. Джеты
Релятивистские джеты проявляют себя во всех диапазонах электромагнитного спектра. Движущиеся по спектру эмиссионные линии водорода и гелия имеют сложный профиль и сильно переменны, что свидетельствует о клочковатой структуре джетов. Оптическое излучение джетов в линиях возникает на расстоянии примерно 1015 см от центрального источника, где температура плазмы опускается до 104 К. Однако на малых расстояниях внутри орбиты двойной звездной системы температура вещества джетов достигает сотен млн. К. О наличии такой высокотемпературной плазмы у основания джетов впервые узнали из анализа рентгеновских спектров, полученных на ИСЗ «Экзосат» в середине 80-х годов. В этих спектрах присутствовала линия излучения, принадлежащая ионизованным до гелиеподобного состояния атомам железа (Fe XXV). В таком состоянии возле ядра остается только два электрона. Линия возникает в результате перехода электронов с первого возбужденного уровня на основной. Испускаемые при этом кванты в лабораторной системе отсчета имеют энергию 6,7 кэВ. Эта линия смещалась по спектру с тем же периодом 163 дня, как и оптические линии. Более того, совпали и амплитуды этих смещений. Тем самым кинематическая модель джетов была подтверждена вплоть до расстояний от источника порядка 1012 см. Еще более интригующими оказались результаты рентгеновских наблюдений, проведенных ИСЗ «Гинга» в 1987–1989 гг. Во-первых, в несколько раз возросла полная рентгеновская светимость компактного источника, а спектр стал жестче. Во-вторых, как
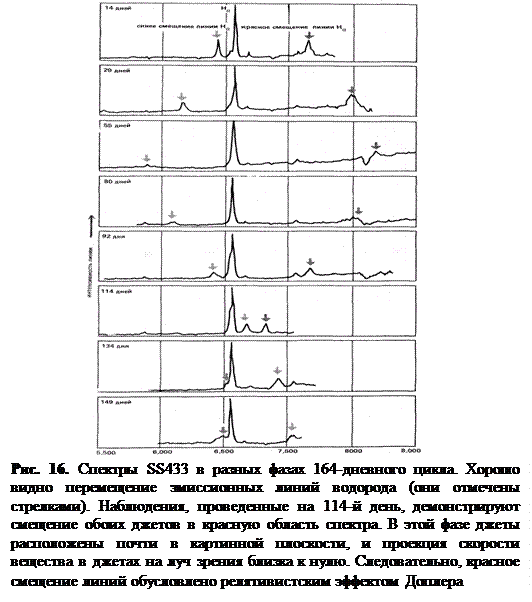 |
обнаружил Н. Каваи, структура эмиссионной рентгеновской линии железа оказалась более, сложной.
В спектре присутствовала широкая линия, положение которой (около 7 кэВ) не изменялось с фазой прецессионного цикла. Эта компонента принадлежит переходам между первым возбужденным и основным уровнем уже водородоподобного (Ре XXVI) железа. Отсутствие заметного смещения с фазой прецессионного цикла говорит о том, что широкая линия формируется не в джете, а преимущественно в квазисферической оболочке, не участвующей в релятивистском движении. Кроме этого, в спектре наблюдалась узкая компонента, энергия которой периодически изменялась с фазой прецессии, т. е. эта линия рождалась в релятивистском джете и принадлежала атомам железа, находящимся в более низких стадиях ионизации. По наблюдениям с ИСЗ «Гинга» впервые были получены кривые блеска рентгеновских затмений. Эти затмения возникают в результате покрытия оптической звездой горячих областей квазисферической оболочки и основания джетов. Как следует из анализа этих затмений, большая часть рентгеновского излучения выходит из области с размером порядка 0,1 расстояния между компонентами двойной системы. Длительность рентгеновских затмений позволяет оценить отношение масс в системе.
3.3. Модель SS 433
Главное, что отличает SS 433 от других систем с перетеканием вещества на компактный объект, и с чем связаны феномены этого источника – это огромная скорость поступления вещества в аккреционный диск. При такой скорости устанавливается режим сверхкритической дисковой аккреции. В чем же здесь дело?
Как известно, при дифференциальном
кеплеровском вращении вещества, которое устанавливается в аккреционном диске
вокруг компактного объекта, за счет некоторых механизмов вязкости (в основном,
турбулентности) происходит выделение энергии и потеря момента количества движения. В результате этого вещество оседает на тяготеющий центр. На больших
расстояниях от тела с массой М светимость диска вне радиуса R
оказывается равной 3/2 GMM/R, где G=6,67·10-7
см3с-2г-1 – гравитационная постоянная, М
– скорость аккреции. С приближением к центру при данном темпе аккреции
энерговыделение возрастает. С другой стороны, оно не может превысить некоторый
предел, называемый Эддингтоновским пределом светимости. Эта светимость для центральной
массы порядка солнечной примерно равна 1038 эрг/с. На расстояниях около
10 км (радиус нейтронной звезды или последняя устойчивая круговая орбита вокруг
черной дыры солнечной массы) Эддингтоновский предел достигается при темпах
аккреции порядка 10-8 ![]() /год.
[12].
/год.
[12].
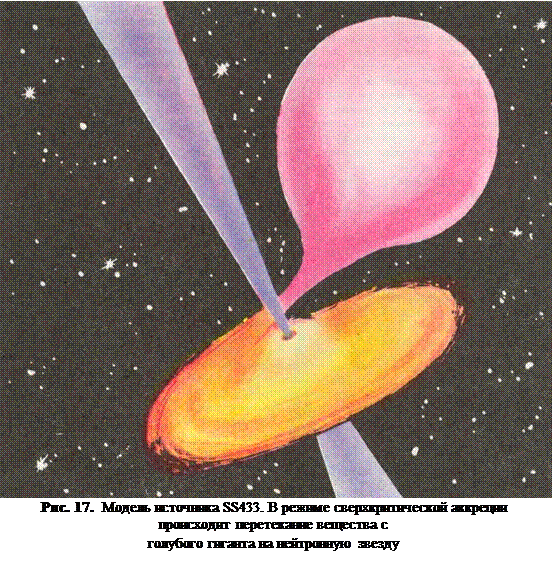 |
Светимость обычных двойных рентгеновских источников, как правило, меньше Эддингтоновского предела и соответственно темп аккреции меньше 10-8
 |
Однако при характерном для SS 433 темпе втекания вещества в диск (10-5
При определенных условиях в центре диска могут возникнуть две противоположно направленные воронки, которые и направляют релятивистские джеты. Откуда же возьмутся джеты? Как представляется, небольшой градиент давления вблизи поверхности центрального источника вполне достаточен, чтобы вещество вырывалось с параболической скоростью (а это как раз 0,3–0,5 скорости света для нейтронной звезды). Важно, что из-за действия вязкости скорость оттока вещества на больших расстояниях от поверхности нейтронной звезды будет практически постоянной (3·103 км/с). При этом центральная оболочка со стороны должна выглядеть совершенно одинаково вне зависимости от того, нейтронная звезда или черная дыра спрятана в ее недрах. Однако, по мнению авторов, небольшой градиент давления вполне может создаться на поверхности быстровращающейся нейтронной звезды со слабым магнитным полем. Именно наличие такой нейтронной звезды объясняет появление джетов с наблюдаемой скоростью.
Широкая компонента
Оттекающий от центральных частей диска поток неоднороден. Его можно представить разбитым на сгустки холодной и плотной плазмы, движущейся в более горячей и разреженной среде (вроде всплывающих облаков). Перемещение этих «островков» относительно горячей среды разогревает их внешние части. Именно в этой горячей среде в результате фоторекомбинации и возникает широкая и мощная линия водородоподобного железа (энергия линии 6,95– 6,97 кэВ). Характерная температура в области формирования широкой линии порядка 1 кэВ, и высокая степень ионизации железа при такой температуре поддерживается процессами фотопоглощения квантов с энергиями 10 кэВ и выше, которые приходят из более глубоких слоев. Фотоны, испускаемые в линии, несколько раз рассеиваются на горячих электронах плазмы, что и создает широкую линию. Затем эти фотоны рассеиваются на более холодных всплывающих островках вещества практически не меняя своей энергии. При этом они проходят дополнительный путь и выходят из оболочки много дальше зоны формирования широкой линии. Именно эта эффективная оболочка с радиусом 0,1 расстояния между компонентами затмевается нормальной звездой. Анализ показывает, что иногда широкая линия железа также частично рождается в джете, однако физически это совсем другая линия – это К-линия низко ионизованного железа с энергией 6,4 кэВ, смещенная до энергии 7 кэВ из-за эффекта Доплера. Она уширяется при рассеянии на горячих электронах в джете, который неоднороден и состоит из отдельных более холодных сгустков, окруженных горячей разреженной плазмой. Добавим, что центральная оболочка и джет погружены в еще более разреженную корону (или гало), и даже при полном затмении центральной оболочки и джета мы все-таки наблюдаем остаточное рентгеновское излучение, рассеянное на электронах не затмевающейся короны. Нужная концентрация электронов во внешнем гало поддерживается дополнительной поставкой их при «таянии» всплывающих плотных островков в разреженной плазме внешней короны.
Непрерывное рентгеновское излучение SS 433, которое наблюдалось с борта ИСЗ «Гинга», описывается законом тормозного теплового спектра с температурой 30 кэВ. Это излучение в основном выходит из глубоких слоев центральной оболочки. Конечно, непрерывный спектр образуется и в более высоких, т. е. менее горячих, слоях оболочки, но с меньшей интенсивностью. Часть непрерывного излучения формируется в джете и в моменты понижения светимости центральной оболочки доля излучения от джета возрастает. [23]
3.4. Черная дыра или нейтронная звезда?
Одним из нерешенных вопросов на данный момент остается вопрос о
природе компактного объекта в SS 433.
Соблазнительно видеть в нем кандидата в черные дыры, однако сколь нибудь
надежных доказательств этому пока нет. Что же мы знаем о компактной звезде в SS 433? По кривой лучевых скоростей можно
определить функцию масс двойной звездной системы. Значение полуамплитуды
лучевых скоростей, полученные по линии ионизованного гелия Hell (l-4686 А), имеют большой разброс – от К=195 км/с до К=150
км/с. При этом разброс в функции масс оказывается еще больше: от f = 10,6![]() до f = 4,8
до f = 4,8![]() . Предполагается, что эта «линия формируется непосредственно
вблизи компактного объекта и тем самым ее лучевая скорость совпадает с лучевой
скоростью объекта. Чтобы получить оценку массы этого тела, надо найти отношение
масс в системе.
. Предполагается, что эта «линия формируется непосредственно
вблизи компактного объекта и тем самым ее лучевая скорость совпадает с лучевой
скоростью объекта. Чтобы получить оценку массы этого тела, надо найти отношение
масс в системе.
 |
Это можно сделать из анализа оптических и/или рентгеновских затменных кривых блеска. Оптические кривые блеска дают оценку q»0,8 – 1, а из анализа рентгеновских затмений можно сделать заключение о q»0,25. При этом в первом случае масса компактной звезды заведомо больше 3
Сейчас представляется, что существенная доля оптического излучения выходит из «всплывающих облаков», когда они становятся оптически прозрачными. До этого момента оптическое излучение было как бы «заперто» в оптически непрозрачных облаках. Другими словами, два эффекта – увеличение площади расширяющихся облаков и уменьшение их оптической толщины – дают дополнительный свет из области с размерами больше полости Роша компактного объекта. При моделировании оптических кривых блеска учет этих эффектов позволяет уменьшить относительный размер полости Роша компактной звезды (а следовательно, отношение масс в системе). [3, 17].
3.5. Прецессия джетов
Остается понять причину 164-дневной прецессии джетов. Поскольку в любой модели их коллимация осуществляется некоторой воронкой вещества вокруг центрального тела, прецессировать должна и эта воронка, а, значит, по крайней мере внутренние части аккреционного диска. Если центральный источник – вращающаяся черная дыра, ее прецессия автоматически гарантирует прецессию внутренних частей аккреционного диска. Однако характерные времена этой прецессии невероятно велики. Если же в центре находится нейтронная звезда без сильного магнитного поля, то требуется прецессия всего аккреционного диска. Поскольку мы имеем дело с двойной системой, в которой относительно недавно произошел взрыв одной из компонент как сверхновой, вероятна несоосность оси вращения нормальной звезды, и орбитального углового момента. Во время вспышки сверхновой плоскость орбиты может изменить ориентацию в пространстве, в то время как угловой момент нормальной звезды свою ориентацию в пространстве сохраняет; разумеется, через некоторое время из-за приливного взаимодействия моменты вращения должны стать соосными. В такой ситуации может возникнуть приливная прецессия нормальной компоненты, вследствие чего весь диск также будет прецессировать. К образованию наклонного аккреционного диска может также привести анизотропный прогрев оптической звезды рентгеновским излучением – подобно тому, как это происходит в двойной рентгеновской системе Геркулес Х-1 [21]
Итак, что же представляет собой SS 433? Прежде всего, это сверхкритическая дисковая аккреция на компактный объект (скорее всего, на нейтронную звезду). В режиме сверхкритической дисковой аккреции возникает квазисферическая оттекающая структура с двумя каналами вдоль оси симметрии, перпендикулярными плоскости диска. Дополнительное энерговыделение вблизи поверхности нейтронной звезды создает градиент давления, под действием которого вещество выталкивается вдоль этих каналов. Эта картина в целом напоминает два симметрично расположенных действующих вулкана и выделяемой энергии достаточно, чтобы придать веществу скорость, равную второй космической для нейтронной звезды солнечной массы.
Глава 4. Оценка амплитуды эффекта отражения для рентгеновской звезды звездной системы Her X-1.
В звездных системах часто наблюдается «эффект отражения» одного компонента от другого. Вследствие движения компонентов двойной системы этот эффект обладает периодичностью.
Оценим амплитуду эффекта отражения, если известна светимость компактной
звезды ![]() , светимость нормальной
звезды
, светимость нормальной
звезды ![]() , большая полуось двойной
системы а и радиус нормальной звезды
, большая полуось двойной
системы а и радиус нормальной звезды ![]() .
.
 |
Рассмотрим тесную двойную звездную систему (ТДС) типа SS 433, одна из компонент которой – нормальная звезда, а вторая вырожденная (релятивистский объект, являющийся нейтронной звездой или черной дырой). Как правило, в таких системах оптическая светимость обычной звезды
Пусть ![]() -рентгеновская светимость
релятивисткой компоненты. На единицу площади поверхности сферы радиуса а каждую
секунду от релятивистского объекта приходит энергия
-рентгеновская светимость
релятивисткой компоненты. На единицу площади поверхности сферы радиуса а каждую
секунду от релятивистского объекта приходит энергия
![]() (4.1)
(4.1)
Площадь диска нормальной звезды ![]() .
.
Тогда каждую секунду на поверхность нормальной звезды площадью S приходит от релятивистского объекта энергия:
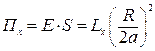 (4.2)
(4.2)
В результате нагрева поверхности звезды этим излучением, она будет испускать дополнительное излучение в оптическом диапазоне:
![]() , (4.3)
, (4.3)
где ![]() - безразмерный
коэффициент пропорциональности.
- безразмерный
коэффициент пропорциональности.
В разные моменты времени наблюдатель будет видеть различную долю нагретой части поверхности.
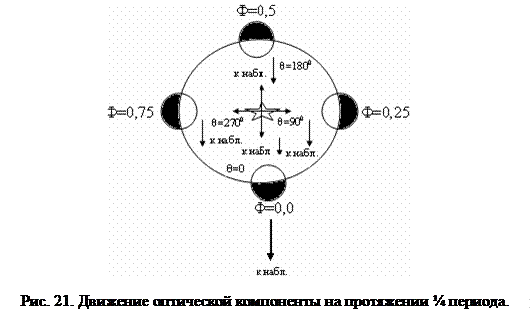 |
Изменение звездной величины и будет являться амплитудой эффекта отражения. Обозначим ее
![]() , (4.4)
, (4.4)
где ![]() -
энергия, излучаемая звездой в фазе
-
энергия, излучаемая звездой в фазе ![]() ,
когда нагретой частью поверхности она повернута от наблюдателя;
,
когда нагретой частью поверхности она повернута от наблюдателя;
а ![]() - энергия
нормальной звезды, излучаемая в фазе
- энергия
нормальной звезды, излучаемая в фазе ![]() ,
когда дополнительно нагретая часть поверхности звезды целиком повернута к
наблюдателю.
,
когда дополнительно нагретая часть поверхности звезды целиком повернута к
наблюдателю.
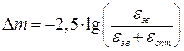 .
(4.5)
.
(4.5)
Т. к. ![]() , поэтому мы пренебрегаем ей
в знаменателе.
, поэтому мы пренебрегаем ей
в знаменателе.
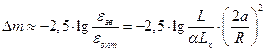 . (4.6)
. (4.6)
Преобразуем выражение (4.6):
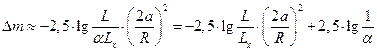 .
.
В итоге мы пришли к такому виду:
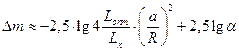 . (4.7)
. (4.7)
Будем считать,
что ![]() и получим итоговую формулу
для амплитуды эффекта отражения:
и получим итоговую формулу
для амплитуды эффекта отражения:
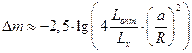 (4.8)
(4.8)
Численную оценку сделаем для рентгеновской двойной системы HZ Her (Her X-1), в
которой ![]() =100,
=100, ![]() =3·1011 см, а=6·1011
см. [13]
=3·1011 см, а=6·1011
см. [13]
Чтобы произвести численную оценку для рентгеновской двойной системы HZ Her подставим в полученную формулу (4.8) данные:
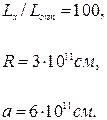
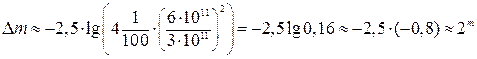
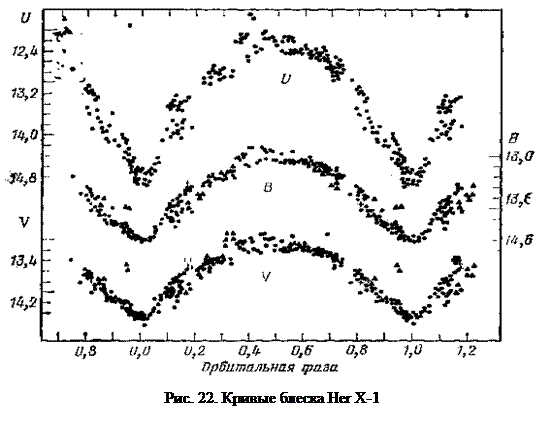 |
Получили, что амплитуда эффекта отражения для рентгеновской звезды звездной системы Her X-1
Заключение
Данная дипломная работа посвящена уникальной по своим свойствам тесной двойной системе SS 433. Источник удивителен по богатству ярких феноменов, физика которых во многом до настоящего времени окончательно не выяснена. SS 433 является оптическим, радио- и рентгеновским источником, с уникальными спектральными свойствами. В оптическом спектре этой звезды наблюдаются три серии эмиссионных линий, соответствующих одним и тем же атомным переходам. Каждая линия серии Бальмера представлена в спектре тремя: «стационарной» и двумя, смещенными в красную и синюю сторону на несколько ангстрем. Смещенные компоненты линий движутся по спектру с периодом 164 дня с амплитудой порядка тысячи ангстрем. «Стационарные» линии также периодически смещаются с гораздо меньшей амплитудой и периодом 13 дней. Блеск звезды меняется с тем же периодом.Нерешен вопрос о природе компактного объекта, что он представляет собой: нейтронную звезду или черную дыру. Существует слишком много теоретических и наблюдательных данных о SS 433, чтобы можно было бы всех их описать. Неизбежно и появление новых путей при решении проблемы.
Есть данные, что кинематическая модель нуждается в некотором исправлении. Астрономы надеются разгадать загадку SS 433 еще до того, как обнаружится четвертый, пятый и шестой его периоды.
Двойные звезды весьма часто встречаются в природе, поэтому их изучение существенно не только для выяснения природы самих звезд, но и для космогонических проблем происхождения и эволюции звезд.
В работе произведена оценка амплитуды для рентгеновской звезды звездной
системы Her X-1
и получен результат: амплитуда эффекта отражения для рентгеновской звезды
звездной системы Her X-1 ![]() , что близко к
наблюдаемой величине.
, что близко к
наблюдаемой величине.
Литература
1. Агекян Т.А. Звезды, галактики, мегагалактика. М.: Наука. 1970. - 256 с.
2. Бакулин П.И., Кононович Э.В., Мороз В.И. Курс общей астрономии. - М.: Наука, 1983. – 560 с.
3. Бисикало Д.В. Как происходит обмен веществом в двойных звездах // Земля и Вселенная. - 1999. - № 1. – С.3-10.
4. Гуревин Л.Э. Чернин А.Д. Происхождение Галактик и звезд. - М.: Наука, 1983. – 192 с.
5. Гурштейн А.А. Известные тайны неба: книга для учащихся. М.: Просвещение, 1984. – 272 с.
6. Дагаев М.М., Демин В.Г., Климин И.А. Чаругин В.М. Астраномия: учебное пособие для студентов физмата. - М.: Просвещение. 1983. - с.384.
7. Дагаев М.М. Задачник – практикум по курсу общей астрономии. – М.: Просвещение, 1965. – 146 с.
8. Затменные переменные звезды / Под ред. В. П. Цесевича. – М.: Наука. Главная редакция физико-математической литературы. 1971. - 350 с.
9. Звезды и звездные системы / Под редакцией Мартынова Д.Я. - М.: Наука, 1981. – 416 с.
10. Каплан С.А. Физика звезд. М.: Наука. 1977. – 208 с.
11. Куликовский П.Г. Справочник задач по астрофизике: Учебное пособие для вузов. – М.: Наука. Главная редакция физико-математической литературы. 1986. - 128 с.
12. ЛипуновВ.М., Сурдин В.Г. Загадка SS 433 // Земля и Вселенная. - 1980. №4. - С. 20-27.
13. Мартынов Д. Я., Липунов В.М. Сборник задач по астрофизике: Учебное пособие для вузов. – М.: Наука. Главная редакция физико-математической литературы. 1986.-128 с.
14. Мартынов Д. Я. Курс общей астрофизики. 3-е изд. М.: Наука. Главная редакция физико-математической литературы. 1979. - 640 с.
15. Соболев В.В. Курс теоретической астрофизики. М.: Наука. 1985. – 504 с.
16. Сурдин В.Г. Рождение звезд: Учебно-научная монография. М.: УРСС. 1997. – 208 с.
17. Физика космоса. Маленькая энциклопедия / Под редакцией Р.А. Сюняев. -М.: Советская энциклопедия. 1986. – 264 с.
18. Черепащук А.М., Лютый В.М. Оптические исследования рентгеновских двойных систем // Земля и Вселенная. - 1986. - № 5. - С. 18-26.
19. Черепащук А.М. Черные дыры новые данные // Земля и Вселенная. - 1992. - №3. - С. 23-32.
20. Черепащук А.М. Черные дыры и звезды Вольфа-Райе // Земля и Вселенная. - 1999. - №3. - С. 26-38.
21. Чернин А.Д. Звезда и физика. М.: Наука. 1984. – 160 с.
22. Шакура Н.И., Постнов К.А. Новое об уникальном объекте SS 433 // Земля и Вселенная. - 1991. № 4. - С. 20-28.
23. . Шакура Н.И., Постнов К.А. Ультратестные двойные звезды // Земля и Вселенная. 1987. - №3. - С. 24-30.
24. Энциклопедия для детей. Астрономия. М.: Аванта 2003. Т.8.

