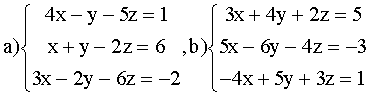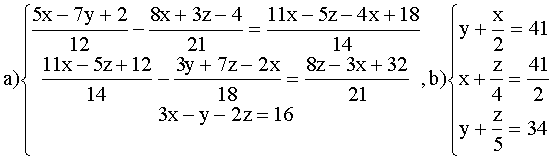Системы
2-х , 3-х линейных уравнений, правило Крамера
ОГЛАВЛЕНИЕ.
1.Краткая теория .
2. Методические рекомендации по выполнению заданий.
3.Примеры выполнения заданий.
4.Варианты заданий.
5.Список литературы.
1. КРАТКАЯ ТЕОРИЯ .
Пусть дана система линейных уравнений
 (1)
(1)
Коэффициенты a11,12,..., a1n, ... , an1 , b2 , ... , bn считаются заданными .
Вектор -строка í
x1 , x2 , ... , xn ý
- называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D
=
ç
A
ê
=
ç
a ij ç
, составленный из коэффициентов при неизвестных , называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи.
a). Если D
¹
0
, то система (1) имеет единственное решение, которое может быть найдено по формулам Крамера : x1= , где
, где
определитель n-го порядка D
i ( i=1,2,...,n) получается из определителя системы путем замены i-го столбца свободными членами b1 , b2 ,..., bn.
б). Если D
=
0
, то система (1) либо имеет бесконечное множество решений , либо несовместна ,т.е. решений нет.
2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
 (2).
(2).
1. В данной системе составим определитель 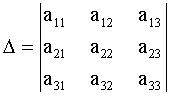 и вычислим.
и вычислим.
2. Составить и вычислить следующие определители :
 .
.
3. Воспользоваться формулами Крамера.

3. ПРИМЕРЫ.
1.  .
.



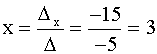
 .
.
Проверка:
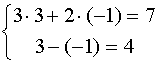 Ответ: ( 3 ; -1 ).
Ответ: ( 3 ; -1 ).
2. 



Проверка:

Ответ: x=0,5 ; y=2 ; z=1,5 .
4. ВАРИАНТЫ ЗАДАНИЙ.
ВАРИАНТ 1.
Решить системы:

ВАРИАНТ 2.
Решить системы:

ВАРИАНТ 3.
Решить системы:
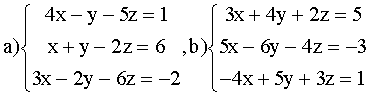
ВАРИАНТ 4.
Решить системы:

ВАРИАНТ 5.
Решить системы:

ВАРИАНТ 6.
Решить системы:

ВАРИАНТ 7.
Решить системы:

ВАРИАНТ 8.
Решить системы:
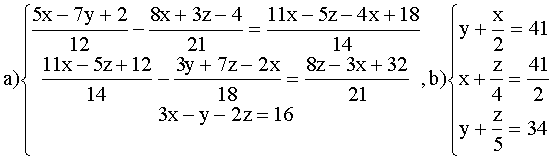
Литература
1. Г.И. КРУЧКОВИЧ. “Сборник задач по курсу высшей математике”, М. “Высшая школа”, 1973 год.
2. В.С. ШИПАЧЕВ. “Высшая математика”, М. “Высшая школа”, 1985 год.
Другие работы по теме:
Расчетные работы по электротехнике
ТипОвая расчетная работа №1. Дано: =110 В =0,2 Ом =0,4 Ом =1 Ом =60 В =50 В Найти: токи в ветвях тремя методами. Решение: Метод законов Кирхгофа. Запишем I закон Кирхгофа для узла А:
Высшая математика. Матрица
Примеры операций над матрицами. Ранг матрицы. Обратная матрица. Системы линейных уравнений. Метод Гаусса для решения систем линейных уравнений, две его составляющие: прямой и обратный ходы. Решение системы по формулам Крамера. Построение параболы.
Вывод формул Крамера
8. Формулы Крамера (рассматривается случай (СЛУ) - определитель системы Если определитель СЛУ отличен от нуля, тогда решение системы определяется однозначно по формулам Крамера:
Математика 2
Вариант 1 Задача 1. Решить систему линейных алгебраических уравнений методом Крамера. x + 2y – z = 2 2x – 3y + 2z = 2 3x + y + z = 8 1 2 -1 Δ = 2 -3 2 = - 3 – 2 + 12 – 9 – 2 – 4 = - 8
Матричная форма формулы Крамера
С.К. Соболев Матричный способ решения СЛАУ, формулы Крамера, свойство присоединенной матрицы и основное свойство линейной зависимости. Рассмотрим
Правила Крамера
ПРАВИЛО КРАМЕРА Рассмотрим систему 3-х линейных уравнений с тремя неизвестными: Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,
Система уравнений по формулам Крамера
Задание № 1 Решить систему уравнений: 1) по формулам Крамера 2) с помощью обратной матрицы 3) методом Гаусса Решение найдем определитель матрицы методом Крамера
Элементы аналитической геометрии
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» ИНСТИТУТ ЭКОНОМИКИ И ВНЕШНЕЭКОНОМИЧЕСКИХ СВЯЗЕЙ
Определитель матрицы 2
Оглавление Задача 2 3 Задача 3 5 Задача 4 7 Задача 1 Вычислить определитель 4-го порядка. Решение: Определитель 4-го порядка находится по формуле: aij – элемент матрицы;
Решение систем линейных уравнений
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТОРГОВО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ
Задачи по Математике
ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ Задачи № 1-10. Решить систему линейных алгебраических уравнений тремя способами: 1) методом Крамера, 2) с помощью обратной матрицы, 3) методом Гаусса.
Основы высшей математики
Построение подмножеств и диаграмм Венна по заданному универсальному множеству и его составляющим. Сложение, вычитание и транспонирование матриц. Метод понижения порядка и приведения системы к треугольному виду. Методы Крамера, Гаусса и матричный способ.
Системы линейных уравнений и неравенств
Основные понятия теории систем уравнений. Метод Гаусса — метод последовательного исключения переменных. Формулы Крамера. Решение систем линейных уравнений методом обратной матрицы. Теорема Кронекер–Капелли. Совместность систем однородных уравнений.
Решение линейной системы уравнений с тремя неизвестными
Решение системы линейных уравнений двумя способами: по формулам Крамера и методом Гаусса. Решение задачи на нахождение производных, пользуясь правилами и формулами дифференцирования. Исследование заданных функций методами дифференциального исчисления.
Математика
Математика и информатика. Решение системы линейных алгебраических уравнений методом Крамера. Работа в текстовом редакторе MS WORD. Рисование с помощью графического редактора. Определение вероятности. Построение графика функции с помощью MS Excel.
Алгебра матриц. Системы линейных уравнений
Выполнение действий над матрицами. Определение обратной матрицы. Решение матричных уравнений и системы уравнений матричным способом, используя алгебраические дополнения. Исследование и решение системы линейных уравнений методом Крамера и Гаусса.
Метод Крамера
Министерство рыбного хозяйства Владивостокский морской колледж ТЕМА: “ Системы 2-х , 3-х линейных уравнений. Правило Крамера. ” г. Владивосток
по Алгебре и геометрие
Федеральное агентство связи Сибирский Государственный Университет Телекоммуникаций и Информатики Межрегиональный центр переподготовки специалистов
Основы высшей матиматики
Вычисление определителя 4-го порядка, математическое решение системы методами матрицы, Крамера и Гаусса. Характеристика понятий невырожденной и обратной, транспонированной и присоединенной матрицы, нахождение алгебраических дополнений элементов таблицы.
Определитель матрицы
Вид в матричной форме, определитель матрицы, алгебраического дополнения и всех элементов матрицы, транспоная матрица. Метод Крамера, правило Крамера — способ решения квадратных систем линейных алгебраических уравнений с определителем основной матрицы.
Определители. Решение систем линейных уравнений
Определители второго и третьего порядков, свойства определителей. Два способа вычисления определителя третьего порядка. Теорема разложения. Теорема Крамера, которая дает практический способ решения систем линейных уравнений используя определители.
Системы линейных уравнений
Решение системы линейных уравнений по правилу Крамера и с помощью обратной матрицы. Нахождение ранга матрицы. Вычисление определителя с помощью теоремы Лапласа. Исследование на совместимость системы уравнений, нахождение общего решения методом Гауса.
Система линейных уравнений
Общий вид системы линейных уравнений и ее основные понятия. Правило Крамера и особенности его применения в системе уравнений. Метод Гаусса решения общей системы линейных уравнений. Использование критерия совместности общей системы линейных уравнений.
Решение произвольных систем линейных уравнений
Рассмотрение систем линейных алгебраических уравнений общего вида. Сущность теорем и их доказательство. Особенность трапецеидальной матрицы. Решение однородных и неоднородных линейных алгебраических уравнений, их отличия и применение метода Гаусса.
Исследования и теории Габриеля Крамера
Преподавательская работа швейцарского математика Габриэля Крамера, введение в анализ алгебраических кривых. Система произвольного количества линейных уравнений с квадратной матрицей Крамера. Классификация и порядок математических и алгебраических кривых.
Крамер, Габриэль
Габриэ́ль Кра́мер (нем. Gabriel Cramer, 31 июля 1704, Женева, Швейцария—4 января 1752, Баньоль-сюр-Сез, Франция) — швейцарский математик, ученик и друг Иоганна Бернулли, один из создателей линейной алгебры.
Моделирование структурных схем в среде SIMULINK пакета MATLAB
Практические навыки моделирования структурных схем в среде SIMULINK пакета MATLAB. Построение графиков функций в декартовой системе координат. Решение систем линейных и нелинейных уравнений. Работа с блоками Sum, Algebraic Constraint, Gain, Product.
 (1)
(1) , где
, где (2).
(2).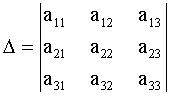 и вычислим.
и вычислим. .
.
 .
.


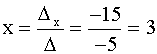
 .
.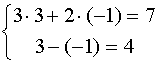 Ответ: ( 3 ; -1 ).
Ответ: ( 3 ; -1 ).